CIEECAU第三章离散时间系统的时域分析本章重点1.离散信号的运算和离散时间系统的基本特性2.求解差分方程所需的边界条件的确定方法3.差分方程的零输入解和零状态解4.离散信号的卷积运算例3.1已知离散信号x(n)和f(n)分别如图3.1.1(a)和(b)所示,画出并标明下列各信号图形(a) x(2n)(b) x(n)(c) J(n)=x(n-1)-f(n-3)(d)y(n)=1+2)f(2-2n)(e) Vx(n)(f) (n)=4(m)3(b)(a)图31.1解离散信号的运算包括相加、相乘、平移、反褶、差分和累加,本例是这些运算方法的应用综合.如图3.1.2所示
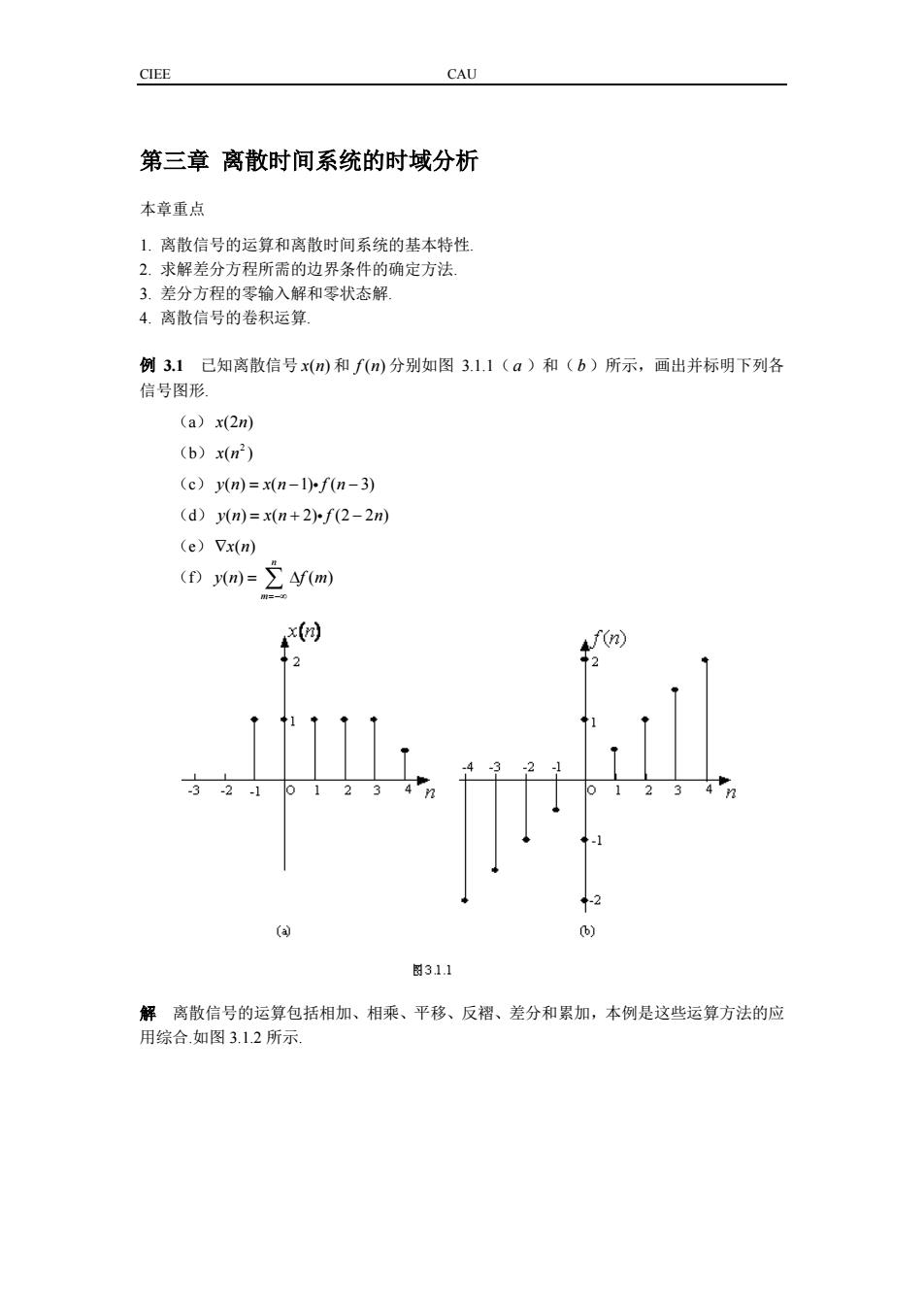
CIEE CAU 第三章 离散时间系统的时域分析 本章重点 1. 离散信号的运算和离散时间系统的基本特性. 2. 求解差分方程所需的边界条件的确定方法. 3. 差分方程的零输入解和零状态解. 4. 离散信号的卷积运算. 例 3.1 已知离散信号 x( ) n 和 f ( ) n 分别如图 3.1.1( a )和(b )所示,画出并标明下列各 信号图形. (a) x(2 ) n (b) 2 x( ) n (c) yn xn f n ( ) ( 1) ( 3) =− − i (d) yn xn f n ( ) ( 2) (2 2 ) =+ − i (e)∇x( ) n (f) () ( ) n m yn f m =−∞ = ∆ ∑ 解 离散信号的运算包括相加、相乘、平移、反褶、差分和累加,本例是这些运算方法的应 用综合.如图 3.1.2 所示
CIEECAU(a)x(2n)(b)x(n)x(2n)x(n))-3-2(a(d)x(n+2) f(2-2n)(c)x(n-1)f(n-x(n-1)f(n-3)n+2):f(2-2mFsanO1-1(d)e)Vx(n)=(n)-x(n-I)+(e)
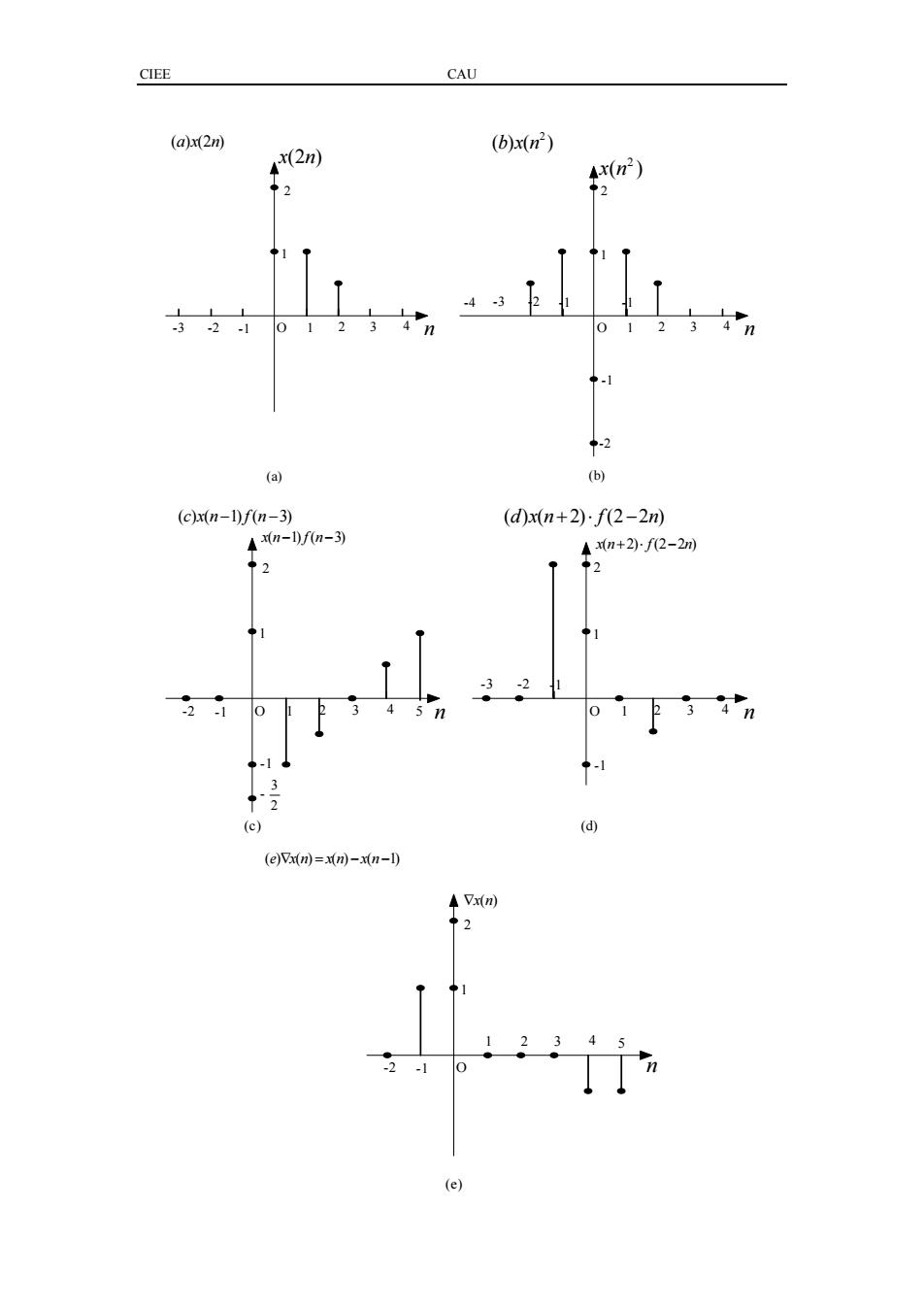
CIEE CAU -3 -2 -1 O 1 2 3 4 n x n (2 ) -3 -2 -1 O 1 2 3 4 n 2 x n( ) -4 1 2 2 1 -1 -2 (a) (b) -1 ( ) (2 ) ax n 2 ()( ) bxn -2 -1 O 1 2 3 4 n -3 -2 -1 O 1 2 3 4 n 1 2 2 1 -1 (c) (d) ( ) ( 1) ( 3) cxn f n − − ( ) ( 2) (2 2 ) d xn f n +⋅ − xn f n ( 1) ( 3) − − xn f n ( 2) (2 2 ) +⋅ − 5 -1 3 2 - -2 -1 1 23 4 O n 1 2 (e) 5 ( ) ( ) ( ) ( 1) e xn xn xn ∇ = −− ∇x n( )

CTE)24(m-2[(m+1)-(mAfimAf(n)(f)图3.12例3.2若离散系统的输入和输出分别为x(n)和y(n),说明下列各系统是否为(i)线性的,ii)非移变的,(ii)因果的,(iv)稳定的.这些系统为(a) y(n)=e(n)(b) (n)=x(n-1)-x(1-n)() (n)= x(m)x(n)nz(d) (n)=Jgn=0x(n+1)n≤-1金(a) y(n)=er((i) (n)=e(n)Y(n)=e*(n)y(n)+y (n)=es(m) +et() *e(()所以,系统是非线性的,(i) 由(n)=e(n) 当输入x(n)=x(n-n)时,(n)=e(-%) = (n-n)所以,系统是非移变的(ii)由于y(n)=e(n)的值与x(n)的未来值无关,因而不能预期未来,所以系统实因果
CIEE CAU 例 3.2 若离散系统的输入和输出分别为 x( ) n 和 y n( ) ,说明下列各系统是否为 (i)线性的, (ii)非移变的, (iii)因果的, (iv)稳定的. 这些系统为 (a) ( ) ( ) x n yn e = (b) yn xn x n ( ) ( 1) (1 ) = −− − (c) 3 1 () ( ) n m n yn xm + = − = ∑ (d) () 1 () 0 0 ( 1) 1 xn n yn n xn n ≥ = = + ≤− 解 (a) ( ) ( ) x n yn e = (i) 1 ( ) 1 ( ) x n yn e = 2 ( ) 2 ( ) x n yn e = 1 2 12 () () () ( ) 1 2 () () xn x n xn x n yn y n e e e + + =+≠ 所以,系统是非线性的. (ii)由 ( ) ( ) x n yn e = 当输入 1 0 x () ( ) n xn n = − 时, 0 ( ) 1 0 () ( ) xn n y n e yn n − = =− 所以,系统是非移变的. (iii)由于 ( ) ( ) x n yn e = 的值与 x( ) n 的未来值无关,因而不能预期未来,所以系统实因果

CIEECAU的(iv)y(n)=e(")不是线性非移变系统,故只能用BIBO原则判别,若x(n)<M,则[>(m)-=ler]<er所以,系统为稳定系统。(n)=x(n-1)-x(I-n)(b)(i)设i(n)=x(n-1)-x(1-n)y(n)=x(n-I)-x(1-n)则(n)+y(n)=x(n-1)+x,(n-1)[(1-n)+x(1-n)]所以系统是线性的(ii) 当x(n)=x(n-ng)时y(n)=x(n-ng-1)-x(1-n-no)=x(n-ng-1)-x[1-(n+n0)]而y(n-no)=x(n-ng -1)-x[1-(n-no)+y(n)所以,系统是移变的.这里要注意的是系统(n)=x(-n)的物理意义是输入序列反褶(ii)由于yi(n)=x(1-n)是非因果的,所以系统y(n)=x(n-1)-x(1-n)是非因果的.(iv)显然,若x(n)是有限的,则(n)也是有限的,所以,系统是稳定的。用同样的方法,可对(3)和(4)系统进行分析,得到以下结果:() =(m)为线性、非移变、非因果、稳定的系统x(n)n≥1(d) (n)=Jon=0[x(n-1 n≤-1为线性、移变、非因果、稳定的系统在教学中,本例所及内容往往是比较容易出差错的,只有在完全理解系统特性的真正含义的基础上,加强练习,才能熟练掌握解题的思路和技巧.读者不妨可以详细解答一下本例的第(c)和(d)小题例3.3某线性非移变因果离散系统由差分方程(n)-(n-1)-2y(n-2)=x(n)+2x(n-2)描述,若x(n)=e(n)且(-1)=2, (-2)=-→试求解以上方程
CIEE CAU 的。 (iv) ( ) ( ) x n yn e = 不是线性非移变系统,故只能用 BIBO 原则判别,若 x( ) n M< ,则 ( ) ( ) x n M yn e e = < 所以,系统为稳定系统。 (b) yn xn x n ( ) ( 1) (1 ) = −− − (i)设 11 1 yn xn x n ( ) ( 1) (1 ) = −− − 22 2 yn xn x n ( ) ( 1) (1 ) = −− − 则 121 2 yn y n xn x n ( ) ( ) ( 1) ( 1) + = −+ − [ ] 1 2 − −+ − x (1 ) (1 ) nx n 所以系统是线性的 (ii)当 1 0 x () ( ) n xn n = − 时 1 10 1 0 yn xn n x n n ( ) ( 1) (1 ) = − − − −− = − − − − + x10 1 0 ( 1) 1 nn x nn ( ) 而 yn n xn n x n n y n ( ) ( 1) 1 ( ) − = − − − − − ≠ 0 0 01 ( ) 所以,系统是移变的.这里要注意的是系统 yn x n () ( ) = − 的物理意义是输入序列反褶. (iii)由于 1 yn x n ( ) (1 ) = − 是非因果的,所以系统 yn xn x n ( ) ( 1) (1 ) = −− − 是非因果的. (iv)显然,若 x( ) n 是有限的,则 y n( ) 也是有限的,所以,系统是稳定的. 用同样的方法,可对(3)和(4)系统进行分析,得到以下结果: (c) 3 1 () ( ) n m n yn xm + = − = ∑ 为线性、非移变、非因果、稳定的系统. (d) () 1 () 0 0 ( 1) 1 xn n yn n xn n ≥ = = − ≤− 为线性、移变、非因果、稳定的系统. 在教学中,本例所及内容往往是比较容易出差错的,只有在完全理解系统特性的真正含 义的基础上,加强练习,才能熟练掌握解题的思路和技巧.读者不妨可以详细解答一下本例 的第(c)和(d)小题. 例3.3 某线性非移变因果离散系统由差分方程 yn yn yn xn xn ( ) ( 1) 2 ( 2) ( ) 2 ( 2) − −− − = + − 描述,若 x() () n n = ε 且 1 2 y y ( 1) 2, ( 2) − = − =− 试求解以上方程

CIECAU解:求解差分方程可分为时域求解和乙域求解,也可以时域和Z域相结合求解,时域求解有选代法、经典法和卷积法。一般选代法不普遍使用,经典法是先求齐次解和特解,在根据边界条件求待定系数,因此,关键在于特解得确定和一组边界条件的求取,本例着重讨论边界条件的求取,在例3.4中,我们把讨论的重点放在特解得确定方面在本例中,齐次方程为(n)-(n-1)-2y(n-2)=0特征方程为 a2-α-2=0特征根a =-1,a2 =2所以,齐次解y.(n)为y.(n)=c(-1)"+c,2"下面求特解y,(n),由于x(n)=ε(n),故可选择y.(n)= D,将上式代入所给差分方程的左边,得到D。-D。-2D, =ε(n)-2e(n-2)D--2当n≥2时即y.(n)=-号e(n-2)全解(m)=G(-1)+c,2"-号e(n-2)其中c,和c,由边界条件决定。不过由于方程的右端在激烈x(n)=ε(n)时,变为e(n)+2e(n-2),因此,对于不同的区间,激励信号是不同的,题目所给的(-1)=2,(-2)=-只是起始条件,初始条件应为y(2)和y(3),而不是y(0),J(1),也不是y(0),J(2)。借助原方程和起始条件,利用选代法,我们可以求得y(2),(3)。因为y(n)=(n)+2e(n-2)+ y(n-1)+2y(n-2)y(0) = e(0) + 26(-2)+ y(-1) +2y(-2)=1+2+2×(-)=2(1) = 8(I) + 26(-1)+ y(0) +2y(-1)2Y(2) = 8(2)+ 26(0)+ ()+2y(0)=1+2×1+7+2×2=14y(3) = 8(3) + 2e(1) + y(2) + 2y(1)
CIEE CAU 解 求解差分方程可分为时域求解和 Z 域求解,也可以时域和 Z 域相结合求解,时域求解 有迭代法、经典法和卷积法。一般迭代法不普遍使用,经典法是先求齐次解和特解,在根据 边界条件求待定系数,因此,关键在于特解得确定和一组边界条件的求取,本例着重讨论边 界条件的求取,在例 3.4 中,我们把讨论的重点放在特解得确定方面. 在本例中,齐次方程为 yn yn yn ( ) ( 1) 2 ( 2) 0 − −− − = 特征方程为 2 a a −−= 2 0 特征根 1 2 a a =− = 1, 2 所以,齐次解 ( ) e y n 为 1 2 ( ) ( 1) 2 n n e yn c c =−+ 下面求特解 ( ) s y n ,由于 x() () n n = ε ,故可选择 0 ( ) s yn D= 将上式代入所给差分方程的左边,得到 00 0 DD D n n − −= − − 2 ( ) 2 ( 2) ε ε 当 n ≥ 2 时 0 3 2 D = − 即 3 ( ) ( 2) 2 s yn n = − − ε 全解 1 2 3 ( ) ( 1) 2 ( 2) 2 n n yn c c n = −+ − − ε 其中 1 c 和 2 c 由边界条件决定. 不过由于方程的右端在激烈 x() () n n = ε 时,变为 ε ( ) 2 ( 2) n n + − ε ,因此,对于不同的区间,激励信号是不同的,题目所给的 1 ( 1) 2, ( 2) 2 y y − = − =− 只是起始条件,初始条件应为 y(2) 和 y(3) ,而不是 y(0) , y(1) ,也 不是 y(0) , y(2)。 借助原方程和起始条件,利用迭代法,我们可以求得 y(2), y(3) 。因为 yn n n yn yn ( ) ( ) 2 ( 2) ( 1) 2 ( 2) = ε + − + −+ − ε y yy (0) (0) 2 ( 2) ( 1) 2 ( 2) = ε + −+ −+ − ε 1 122 2 2 = + + ×− = y yy (1) (1) 2 ( 1) (0) 2 ( 1) = ε + −+ + − ε =1222 7 ++×= y yy (2) (2) 2 (0) (1) 2 (0) = ε + ++ ε =1 2 1 7 2 2 14 + ×+ + × = y yy (3) (3) 2 (1) (2) 2 (1) = ε + ++ ε