
CIE第四章连续信号的傅利叶分析本章重点(1)计算周期信号的频谱(2)灵活运用傅利叶变换有关性质对信号进行正、逆变换;(3)正确理解与运用傅利叶变换的某些性质,如时移一尺度变换,微分积分性质;(4)掌握抽样信号频谱的计算及抽样定理。例4.1已知f()的波形图如图4.1.1所示,试求其傅利叶级数表示式。6-5-4-3-2-101234567图4.1.1解对于周期信号,我们可以用不同的方法求其傅利叶级数。可以用定义求,也可以利用傅利叶级数的某些性质(如微积分性质)求解,还可以借助单周期信号的傅利叶变换与周期信号的傅利叶级数的关系求解。[方法一]直接利用定义求解C+2)"d+(2-te"aF(n)-,r(0)e"d =当n≠0时,对上式分部积分并化简,得sin(n),n*0F," (nn)"(3)当n=0时,F(n)-,r(0)dt=2故有1mF,=--F.所以sin(学r()=2, 6L. (n元)例4.2设有周期矩形脉冲(),脉冲宽度T,幅度为A,周期为7の=。女图3.2.1所示:
CIEE CAU 第四章连续信号的傅利叶分析 本章重点 (1) 计算周期信号的频谱 (2) 灵活运用傅利叶变换有关性质对信号进行正、逆变换; (3) 正确理解与运用傅利叶变换的某些性质,如时移—尺度变换,微分积分性质; (4) 掌握抽样信号频谱的计算及抽样定理。 例 4.1 已知 f ( )t 的波形图如图 4.1.1 所示,试求其傅利叶级数表示式。 解 对于周期信号,我们可以用不同的方法求其傅利叶级数。可以用定义求,也可以利 用傅利叶级数的某些性质(如微积分性质)求解,还可以借助单周期信号的傅利叶变换与 周期信号的傅利叶级数的关系求解。 [方法一]直接利用定义求解: ( ) ( ) ( ) ( ) = = + + − ∫ ∫ ∫ − − − − − 2 0 3 0 2 3 3 3 3 2 2 6 1 6 1 F n f t e dt t e dt t e dt j nt j nt j nt π π π 当 n ≠ 0 时,对上式分部积分并化简,得: ( ) , 0 3 sin 6 2 2 2 ≠ = n n n Fn π π 当 n = 0 时, ( ) ( ) 3 2 6 1 3 3 = = ∫− F n f t dt 故有 0 0 3 2 l im Fn F n = = → 所以 ( ) ( ) ∑ ∞ =−∞ = n t n j e n n f t 3 2 2 2 3 sin 6 π π π 例 4.2 设有周期矩形脉冲 f ( )t ,脉冲宽度τ ,幅度为 A ,周期为 = T T π ω 2 。如 图 3.2.1 所示: 图 4 .1 .1 −8 −7 −6 −5 −4 −3 3 4 5 6 7 8 t 2 −2−1 1 2 1 o () f t

CIEEDAIt0图4.2.1试讨论:(a)当T=T(T为常数),T=2T时频谱的变化规律。(包括频谱的带宽1谱线间宽,幅度等。假设T=(b)设T=T,保持不变t=时频谱的变化规律。解周期矩形脉冲的傅利叶级数系数为Fn=JiAe"n'di-()(o-)2A-sin noorno.TA sin norn元可知F,为实数。而no,tino10=元2m(a)若tT=T,则F(m)-4()若t=,T=2T,则
CIEE CAU 试讨论: (a)当T = T1(T 为常数), 1 T = 2T ,T → ∞ 时频谱的变化规律。(包括频谱的带宽, 谱线间宽,幅度等。假设 4 T1 τ = ) (b)设T = T1 保持不变 4 T1 τ = , 8 T1 τ = 时频谱的变化规律。 解 周期矩形脉冲的傅利叶级数系数为 π ω τ ω ω τ τ ω τ τ τ π n n A n T n A n sa T A Fn Ae dt t T jn 2 sin 2 2 sin 2 0 0 0 0 2 2 2 ⋅ = ⋅ = = = ∫− − ⋅ ⋅ = T π ω 2 0 可知 Fn 为实数。 而 ( ) jn t e n n A f t 0 2 sin ω0τ ω π∑ ∞ −∞ = (a)若 4 T1 τ = ,T = T1,则 ( ) = 4 4 nπ sa A F n 若 4 T1 τ = , 1 T = 2T ,则 T −T 2 τ 2 τ − o ( ) f t t 图4.2.1
CCAUF(m)=()n0元的包络。如图3.2.2若T)。为方便起见,只画出TF(n)=AAZ所示:TF.=T)41112元2元4元0[TF.(=2T)22 4 4'oETFT-→图4.2.2由图4.2.2可以看出,当脉宽t固定时,T越大,谱线间隔越小,相当于TF,的包络被越来越密的间隔抽样。当T→时,周期信号变为非周期信号,离频谱也被连续频谱取代。当T固定时,TF的包络与周期无关,所以带宽保持不变,即40=2元_8元。而F.的幅度与周期与周期T成反比关系,即T增大时,T频谱幅度减小
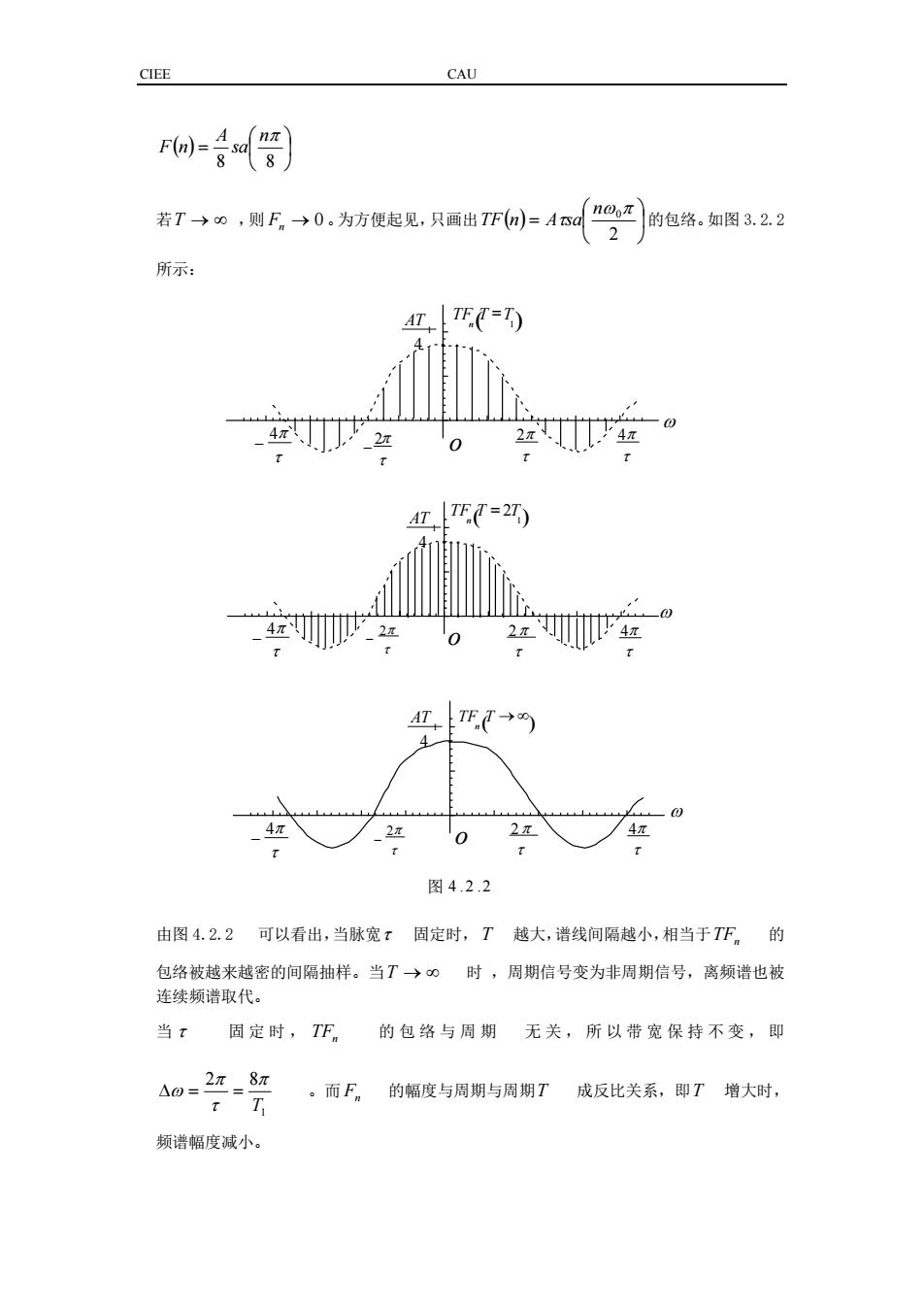
CIEE CAU ( ) = 8 8 nπ sa A F n 若T → ∞ ,则 Fn → 0 。为方便起见,只画出 ( ) = 2 ω0π τ n TF n A sa 的包络。如图 3.2.2 所示: 由图 4.2.2 可以看出,当脉宽τ 固定时, T 越大,谱线间隔越小,相当于TFn 的 包络被越来越密的间隔抽样。当T → ∞ 时 ,周期信号变为非周期信号,离频谱也被 连续频谱取代。 当 τ 固定时, TFn 的包络与周期 无关,所以带宽保持不变,即 1 2 8 T π τ π ∆ω = = 。而 Fn 的幅度与周期与周期T 成反比关系,即T 增大时, 频谱幅度减小。 τ 2π − τ 2π − τ 2π τ 2π 图 4 .2 .2 τ 4π τ 4π τ 4π − τ 4π − o o ( 1) TF T 2T n = ( ) TF T →∞ n 4 1 AT 4 1 AT τ 4π τ 4π − 4 1 AT ω ω ω o τ 2π − τ 2π ( )1 TF T T n =

CAUCIEE(b)若TT=T,则F(a-a()若TT=T,则Fo)=()由于周期T保持不变,因此0=2元保持不变,画出F,如图4.2.3所示。LF.42112元2元14元ommt2元_2元0图4.2.3从图4.2.3可以看出,当T固定时,の。不变,所以谱线间隔相同。81一时,带宽△02元_16元时,带宽の可见脉冲宽度减小时,带宽增大,带宽内包含的频谱分量增多,同时,随着↑减小,频谱包络的幅度值减小。从以上的讨论我们可以得出如下结论:当周期信号的周期增大时,频谱的谱线间隔减小,包络的幅度减小,带宽(这里指主瓣带宽)不变:当周期信号的信号脉宽减小时频谱的谱线间隔不变,包络的幅度减小,带宽增大
CIEE CAU (b)若 4 T1 τ = ,T = T1,则 ( ) = 4 4 nπ sa A F n 若 8 T1 τ = ,T = T1 ,则 ( ) = 8 8 nπ sa A F n 由于周期T 保持不变,因此 T π ω 2 0 = 保持不变,画出 Fn 如图 4.2.3 所示。 从图 4.2.3 可以看出,当T 固定时, ω0不变,所以谱线间隔相同。 4 T1 τ = 时,带宽 1 2 8 T π τ π ∆ω = = 8 T1 τ = 时,带宽 1 2 16 T π τ π ∆ω = = 可见脉冲宽度τ 减小时,带宽增大,带宽内包含的频谱分量增多,同时,随着τ 减 小,频谱包络的幅度值减小。 从以上的讨论我们可以得出如下结论:当周期信号的周期增大时,频谱的谱线间隔减 小,包络的幅度减小,带宽(这里指主瓣带宽)不变:当周期信号的信号脉宽减小时频谱 的谱线间隔不变,包络的幅度减小,带宽增大。 n F τ 2π τ 2π − o ω ω 4 A τ 4π − τ 4π 8 A n F o τ 4π − τ 4π 图 4 .2 .3 τ 2π τ 2π −

CAUCIE例4.3已知信号1+ cos af]/ ≤ tf()=0l >T求该信号的傅利叶变换。解该信号是一个截断函数。我们既可以把该信号看成是周期信号(1+cost)经过门函数Gz()的截取,也可以看成是G2()被信号(1+cost)调制所得的信号。由此有以下三种解法。[方法一]利用频域平移的性质:由于F()=(1+cost)G2(),如果我们把(1+cost)化为虚指数信号,()就可以看成是门函数G,()被虚指数信号调制的结果。在频域上,就相当于对G2()的频谱进行平移。(0)=(1+costi)Gzs()-(e"+je-"G(0)又因G. (0) α 2sin 所以根据频域平移的性质,可得1-2sing(o-1) -2sin (o+1)F(o)=0[r()]- 2sin m0+ 2sin元a0-1+10(0?-1)例4.4已知()的波形图如图4.4.1所示,求T(0)的傅利叶变换F(o)。该信号是梯形波,我们可以把该信号分解为矩形波或三角波等我们熟悉的信号。当然也可以用微分的方法将该信号变为冲激串。10)图44【方法一]利用时域卷积定理我们可以把梯形脉冲看成是两个不同宽度的矩形脉冲()与J;()的卷积,如图4.4.2所示
CIEE CAU 例 4.3 已知信号 ( ) > + ≤ = τ τ t taf t f t 0 1 cos 求该信号的傅利叶变换。 解 该信号是一个截断函数。我们既可以把该信号看成是周期信号(1+ cost) 经过门函数 G ( )t 2π 的截取,也可以看成是G (t) 2π 被信号(1+ cost)调制所得的信号。由此有以下三种解 法。 [方法一] 利用频域平移的性质:由于 f (t) = (1+ cost) G (t) 2π ,如果我们把 ( ) 1+ cost 化为虚指数信号, f ( )t 就可以看成是门函数G (t) 2π 被虚指数信号调制的结果。在频域上, 就相当于对G ( )t 2π 的频谱进行平移。 f () ( ) () t t G t e e G ( )t jt jt 2π 2π 2 1 2 1 1 cos 1 = + = + + − 又因 ( ) ω πω π 2sin G2 t ↔ 所以根据频域平移的性质,可得 ( ) () [ ] ( ) ( ) ( ) 1 2sin 1 2sin 1 2 1 1 2sin 1 2 1 2sin 2 − = − + ⋅ + + − ⋅ − =℘ = + ω ω πω ω π ω ω π ω ω πω F ω f t 例 4.4 已知 f ( )t 的波形图如图 4.4.1 所示,求 f (t)的傅利叶变换 F( ) ω 。 解 该信号是梯形波,我们可以把该信号分解为矩形波或三角波等我们熟悉的信号。当然也 可以用微分的方法将该信号变为冲激串。 [方法一]利用时域卷积定理。 我们可以把梯形脉冲看成是两个不同宽度的矩形脉冲 f (t) 1 与 f (t) 2 的卷积,如图 4.4.2 所示。 图 4 . 4 . 1 −2 2 1 −1 o 1 t ( ) f t