
离散数学试卷(三)参考答案 一、填空20%(每空2分) 1、2x+l)2、{ka,a>,<a,b>,<a,c>,<c,c>,<b,a>,<c,a>y3、 {k2,1>,<3,1>,<5,1>,<4,2>,<62>,<6,3>: 4 6534之321 反对称性、反自反性:4、{他,{中,2}),{2},{D,2,{2)}:5、1: 6、(PV一QVR)A(-PVOVR)A(PVOVR):7、任意x,如果x是素数则存在 个y,y是奇数且y整除x:8、xy:3u(-P(x,)vPy,)vQ(x,y,》。 二、选择20%(每小题2分) 题目123 5678910 答案cc A B D A D c 三、正证明16%(每小趣8分) 1、 ①A P(附加前提 ②AVB T①I ③AVB→CAD ④CAD T②③1 ⑤D ©DVE T⑤I ⑦DvE→F ⑧F T⑥⑦I ⑨A→F CP 3 xPx)v3rQx)台-x)P(x)→3rQx) 本题可证x(P(x)VQ(x》→(xPx)→3xOx)
离散数学试卷(三)参考答案 20 一、 填空 20%(每空 2 分) 1 、 2(x+1) ; 2 、 { a ,a , a ,b , a ,c , c ,c , b ,a , c ,a } ; 3 、 { 2,1 , 3,1 , 5,1 , 4,2 , 6,2 , 6,3 ; 4、 反对称性、反自反性;4、{,{{,2}},{{2}},{{,2},{2}}} ;5、1; 6、(P Q R) (P Q R) (P Q R) ;7、任意 x,如果 x 是素数则存在一 个 y,y 是奇数且 y 整除 x ;8、xyzu(P(x,z) P( y,z) Q(x, y,u)) 。 二、 选择 20%(每小题 2 分) 题目 1 2 3 4 5 6 7 8 9 10 答案 C C C C A B D A D C 三、 证明 16%(每小题 8 分) 1、 ① A P(附加前提) ② A B T①I ③ A B →C D P ④ C D T②③I ⑤ D T④I ⑥ D E T⑤I ⑦ D E → F P ⑧ F T⑥⑦I ⑨ A → F CP 2、 ( ( ) ( )) ( ( ) ( ) ( ) ( ) ( ) ( ) ( ) x P x Q x x P x x Q x x P x x Q x x P x x Q x → → 本题可证

离散数学试卷(三)参考答案 ①-xPx) p(附加前提) ②3x(-P(x) TOE ③P(a) ES② ④x(P(x)vQ(x) ⑤P(a)vQ(a) US④ ⑥Qa) T③⑤I ⑦3r0x) EG⑥ ⑧-(Px)→3xQx) CP 四、14% 1、证明: (I)自反性:<x,y>eX,由于x+y=x+y <xy>,<xy>∈R.R自反 (2)对称性:<x,乃>eX,<x2,2>eX 当<x,y>,<x2,乃2>∈时即x+为2=为2+y也即x2+月=x+乃2 故<x2,2>,<x,y>eR.R有对称性 (3)传递性:廿<x,y>∈X,廿<x2,2>∈X廿<x,乃>∈X 当<x,片>,<x2乃2>eR且<x2乃2>,<x3乃>eR时 取+片=+片) x2+为3=x3+为2(2) (四+(2)x+为2+x2+片=x2+片+x3+2 即x+=x3+ 故<x1,片>,<x,乃>ER.R有传递性 由(1)(2)(3)知:R是X上的先等价关系 21
离散数学试卷(三)参考答案 21 ① (xP(x)) P(附加前提) ② x(P(x)) T①E ③ P(a) ES② ④ x(P(x) Q(x)) P ⑤ P(a) Q(a) US④ ⑥ Q(a) T③⑤I ⑦ xQ(x) EG⑥ ⑧ (xP(x) → xQ(x) CP 四、 14% 1、 证明: (1) 自反性: x, y X, 由于x + y = x + y x, y , x, y R R自反 (2) 对称性: x1 , y1 X , x2 , y2 X 当 x1 , y1 , x2 , y2 R时 1 2 2 1 2 1 1 2 即x + y = x + y 也即x + y = x + y 故 x2 , y2 , x1 , y1 R R有对称性 (3) 传递性: x1 , y1 X , x2 , y2 X x3 , y3 X 当 x1 , y1 , x2 , y2 R 且 x2 , y2 , x3 , y3 R时 + = + + = + (2) (1) 2 3 3 2 1 2 2 1 x y x y x y x y 即 1 2 2 3 2 1 3 2 (1) + (2) x + y + x + y = x + y + x + y 即 1 3 3 1 x + y = x + y 故 x1 , y1 , x3 , y3 R R有传递性 由(1)(2)(3)知:R 是 X 上的先等价关系
离散数学试卷(三)参考答案 2、XR=I<1,2>]R} 五、10% 0100 1010 1、M=0001 关系图 (0000 1010 2Me=M。oM=0101 0000 000o0 (0101) Me-MgoM =101 0 0000 0000 1010 M=MM0 1 0 1 00 0=M MMeM (0000 (1111 Man-M.tNetMe 0001 (0000 t(R)={<a,a>,<a,b>,<a,心,a,d>,b,a>,<b,b>,<b,c.>,<b,d>,<c,d>}。 六、20% 1、(fn8=edom则e domgy=f)Ay=gx =(<x,y>xE domf=f(x)=g(x) 令h-fng .domfg domh=xx e domf domg,f(x)=g(x) (2)h=fx,yxedomfdomgny=h(x)=f(x)=g(x) 对r∈domh若有y,使得 y=h(x)=f(x)=g(x),y2=h(x)=f(x)=g(x)
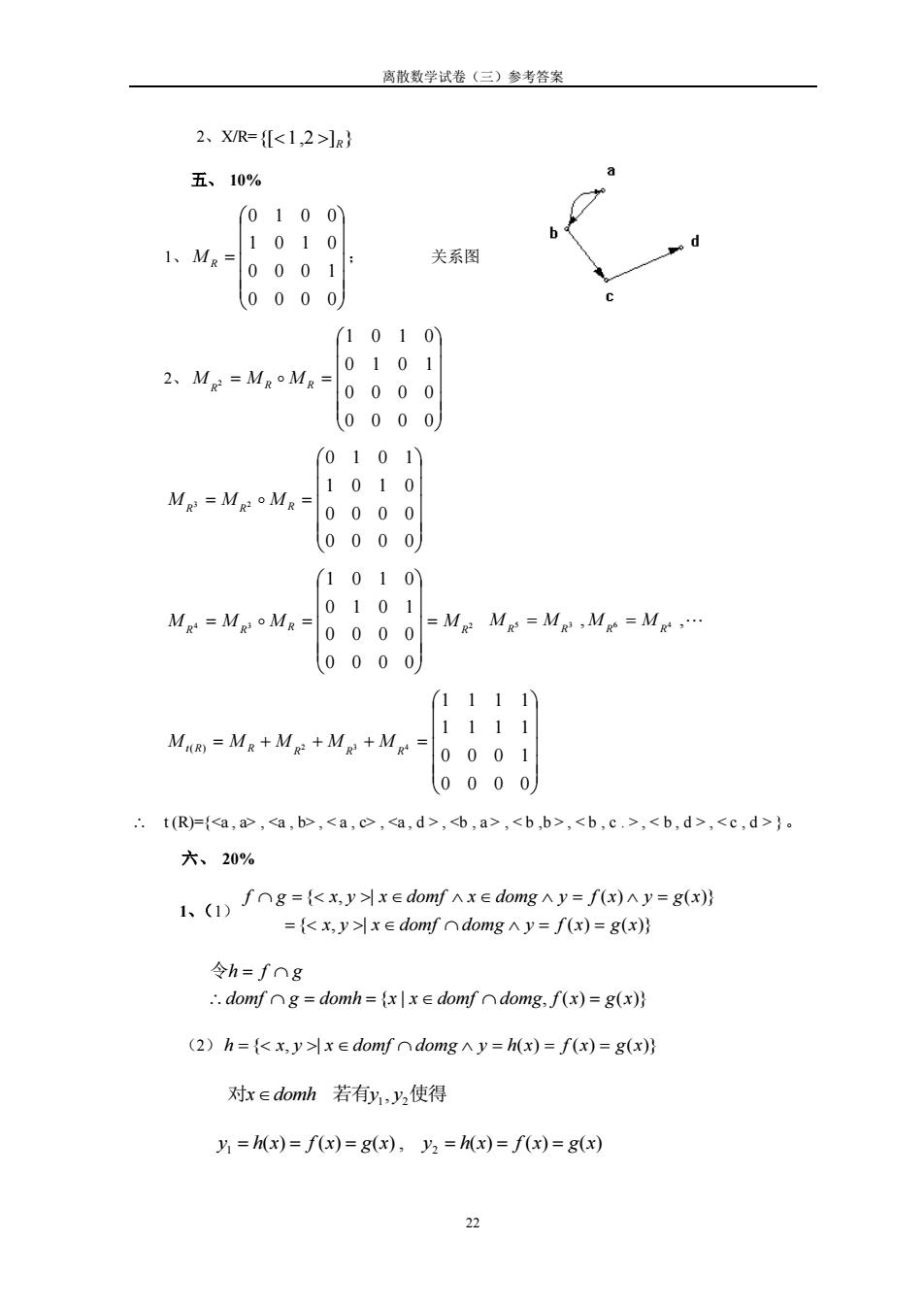
离散数学试卷(三)参考答案 22 2、X/R= {[ 1,2 ] } R 五、 10% 1、 = 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 M R ; 关系图 2、 = = 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 M R 2 M R M R = = 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 1 M R 3 M R 2 M R 4 3 2 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 M R M R M R M R = = = M R 5 = M R 3 ,M R 6 = M R 4 , = + + + = 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 2 3 4 Mt(R) M R M R M R M R t (R)={<a , a> , <a , b> , < a , c> , <a , d > , <b , a > , < b ,b > , < b , c . > , < b , d > , < c , d > }。 六、 20% 1、(1) { , | ( ) ( )} { , | ( ) ( )} x y x domf domg y f x g x f g x y x domf x domg y f x y g x = = = = = = domf g domh {x | x domf domg, f (x) g(x)} h f g = = = 令 = (2) h = { x, y | x domf domg y = h(x) = f (x) = g(x)} 对xdomh 若有y1 , y2使得 ( ) ( ) ( ) , ( ) ( ) ( ) 1 2 y = h x = f x = g x y = h x = f x = g x

离散数学试卷(三)参考答案 由于f(或g)是函数有y=y2即x e domh有唯y使得y=(x) f⌒g也是函数 2、证明: "一"若有一左逆g,则对1∈Tgf0=1 故g。f是入射,所以∫是入射。 "="f是入射,f:T→S定义如下: s∈f(T),由f入射,3teT,使f()=s 此时令g(s)=1,若sEfT)令g(s)=ceT 则对s∈S,g(s)只有一个值1或c且若f)=s 则gf)=gs)=1,故g是f的左逆元 即若入射,必能构造函数g,使g为左逆函数
离散数学试卷(三)参考答案 23 1 2 由于f (或g)是函数,有y = y 即xdomh有唯一y使得y = h(x) f g也是函数。 2、证明: ""若f 有一左逆g ,则对t T g f (t) = t 故 g f是入射,所以 f 是入射。 则 故 是 的左逆元 则对 只有一个值 或 且若 此时令 若 令 由 入射 使 是入射 定义如下 g f t g s t g f s S g s t c f t s g s t s f T g s c T s f T f t T f t s f f T S ( ) ( ) , , ( ) ( ) ( ) , ( ) ( ) ( ), , | , ( ) " " , : : = = = = = = → 即若f入射,必能构造函数g, 使g为f左逆函数