北京邮电大学出版社：21世纪高等学校规划教材《高等数学》课程教学资源（课件讲稿）第1章 函数、极限与连续 第3节 函数的极限

第3为 第一章 益数的极限 对y=f(x),自变量变化过程的六种形式 () x→00 (4)x→x0 (2)x→+0 (5)x→x0 (3)x→-0 (6)x→x0 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束

目录 上页 下页 返回 结束 第一章 第3节 自变量变化过程的六种形式: 函数的极限

第3节 第一章 益数的极限 一、x→o时函数的极限 二、x→x时函数的极限 三、函数极限的性质 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束

目录 上页 下页 返回 结束 第一章 第3节 函数的极限 一、x→∞时函数的极限 二、x→x0时函数的极限 三、函数极限的性质

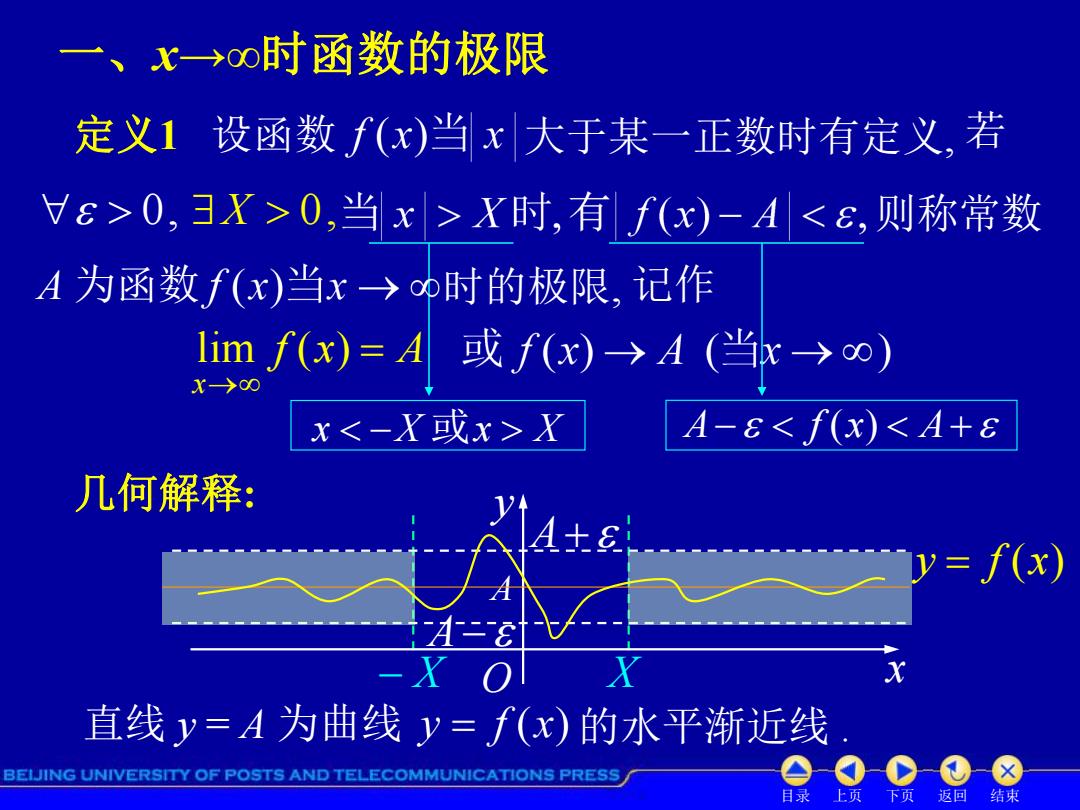
一、x→∞时函数的极限 定义1设函数f(x)当x大于某一正数时有定义，若 >0,3X>0,当x>X时，有f(x)-A<8,则称常数 A为函数f(x)当x→o0时的极限，记作 limf(x)=A或f(x)>A(当x>o) X→00 x<-X或x>X A-8<f(x)<A+8 几何解释： =f(x) 二8 X 直线y=A为曲线y=f(x)的水平渐近线 BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录 上页 下页 返回 结束

目录 上页 下页 返回 结束  X X A  A O x y y  f (x) A 定义1 设函数 大于某一正数时有定义, 若 X  0, 则称常数 时的极限, f x A x   lim ( ) 几何解释: x  X 或x  X A  f (x)  A 记作 直线 y = A 为曲线 的水平渐近线 .   0, A 为函数 一、x→∞时函数的极限

例1.3.1用定义证明 lim-=0. x->ooX Y= 证： X X 故Vs>0,欲使 -0<,只要x> 取X=上，当x>X时，就有 0 <8 因此 1im=0 x→00X 注：y=0为y=的水平渐近线. X BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回结束

目录 上页 下页 返回 结束 例1.3.1 用定义证明 0. 1 lim  x x 证: 0 1  x x 1  取 , 1  X  因此 注: 就有 故   0, 欲使 只要 O x y x y 1 

两种特殊情况： 1imf(x)=A二V8>0,3X>0,当x>X时，有 X>+00 f(x)-AKε 1imf(x)=A二8>0,3X>0,当x<-X时，有 f(x)-A<8 几何意义：直线y=A仍是曲线y=f(x)的渐近线 例如，= g)=1-X y+2 都有水平渐近线y=0, 又如，f(x)=1-2x,g(x)=1+2x 都有水平渐近线y=1. BEIJING UNIVERSITY OF POSTS AND TELECOMMUNICATIONS PRESS 目录上页下页 返回 结

目录 上页 下页 返回 结束 x 1 1 x 1 直线 y = A 仍是曲线 y = f (x) 的渐近线 . 两种特殊情况 : f x A x   lim ( )   0, X  0, 当 时, 有 f (x)  A     0, X  0, 当 x  X 时, 有 f (x)  A   几何意义 : 例如， 都有水平渐近线 y  0; 都有水平渐近线 y 1. 又如