AKD图1.2.6均匀场中放进了介质球的电场图1.2.7均匀场中放进了导体球的电场图1.2.9点电荷位于一块导平面上方的电场图1.2.8点电荷位于一块介质上方的电场
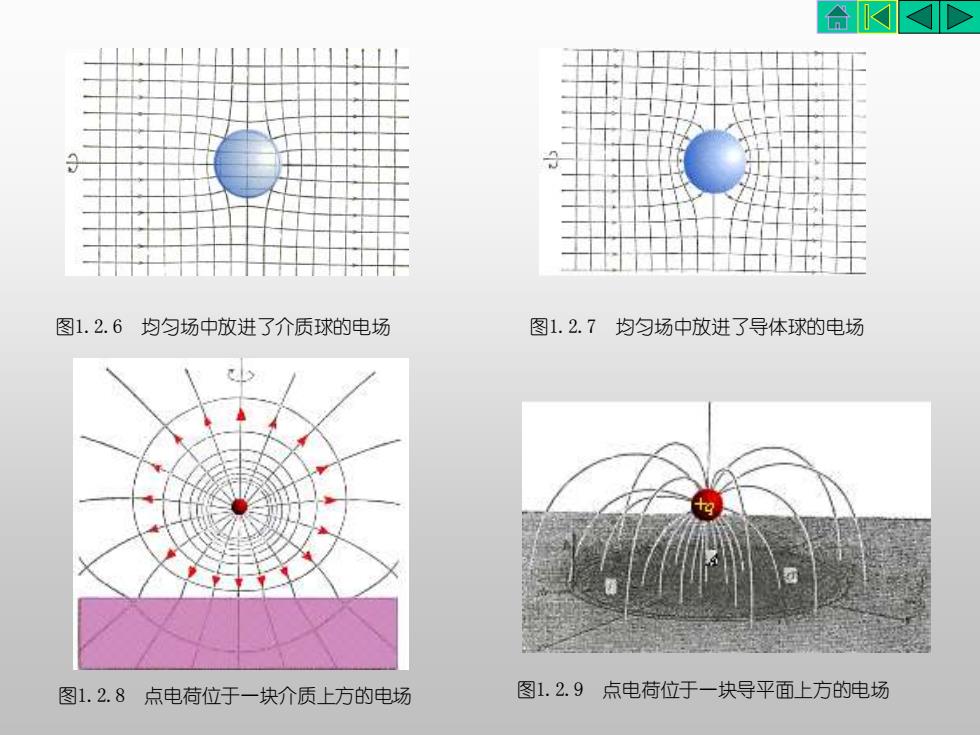
图1.2.6 均匀场中放进了介质球的电场 图1.2.7 均匀场中放进了导体球的电场 图1.2.8 点电荷位于一块介质上方的电场 图1.2.9 点电荷位于一块导平面上方的电场
合KKD1.2.2真空中的高斯定律1. 静电场的散度高斯定律的微分形式p(r')dE(r) :点电荷产生的电场4元8%r-r对上式等号两端取散度;利用矢量恒等式及失量积分、微分的性质,得V.E(r)=P(r)真空中高斯定律的微分形式80其物理意义表示为V.E=p=0V.E=p<0V.E=p>0高斯定律说明了静电场是电荷就是场的散度(通量源),电是一个有源场,!力线从正电荷发出,终止于负电荷
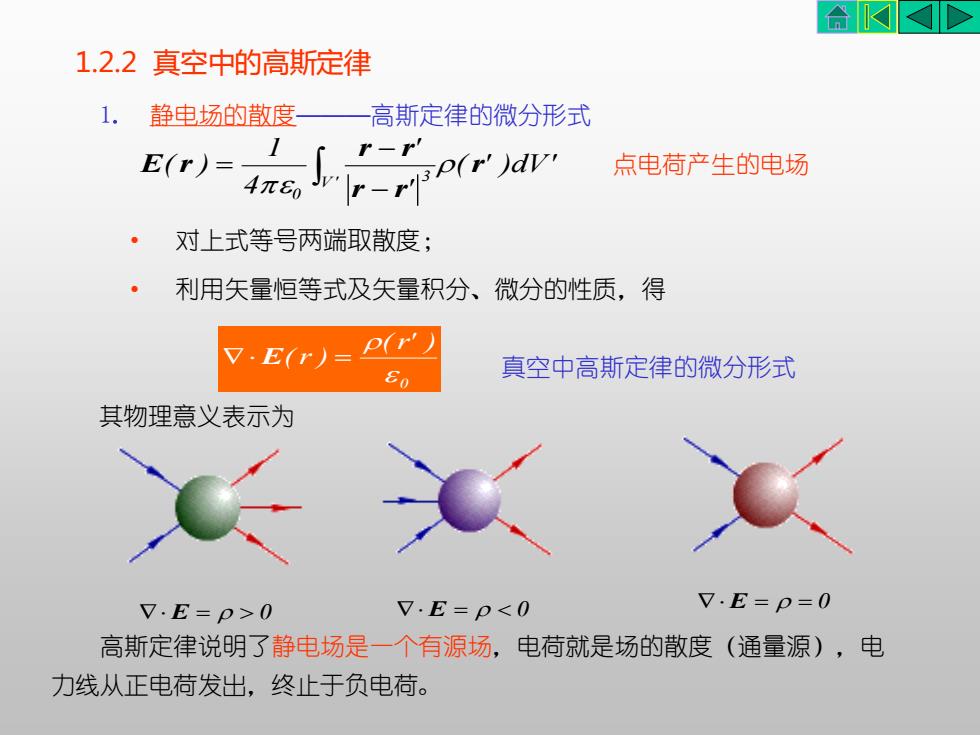
• 对上式等号两端取散度; • 利用矢量恒等式及矢量积分、微分的性质,得 1.2.2 真空中的高斯定律 1. 静电场的散度———高斯定律的微分形式 0 (r' ) (r ) E = 真空中高斯定律的微分形式 ( ' )dV' ' ' 4 1 ( ) V' 3 0 r r r r r E r − − = 点电荷产生的电场 其物理意义表示为 E = = 0 E = 0 E = 0 高斯定律说明了静电场是一个有源场,电荷就是场的散度(通量源),电 力线从正电荷发出,终止于负电荷
AKKD2.高斯定律的积分形式V.Ed-ZqipdyE.ds三-散度定理801=1式中n是闭合面包围的点电荷总数。E的通量仅与闭合面S所包围的净电荷有关。图1.2.11闭合曲面的电通量S面上的E是由系统中全部电荷产生的。图1.2.12闭合面外的电荷对场的影响
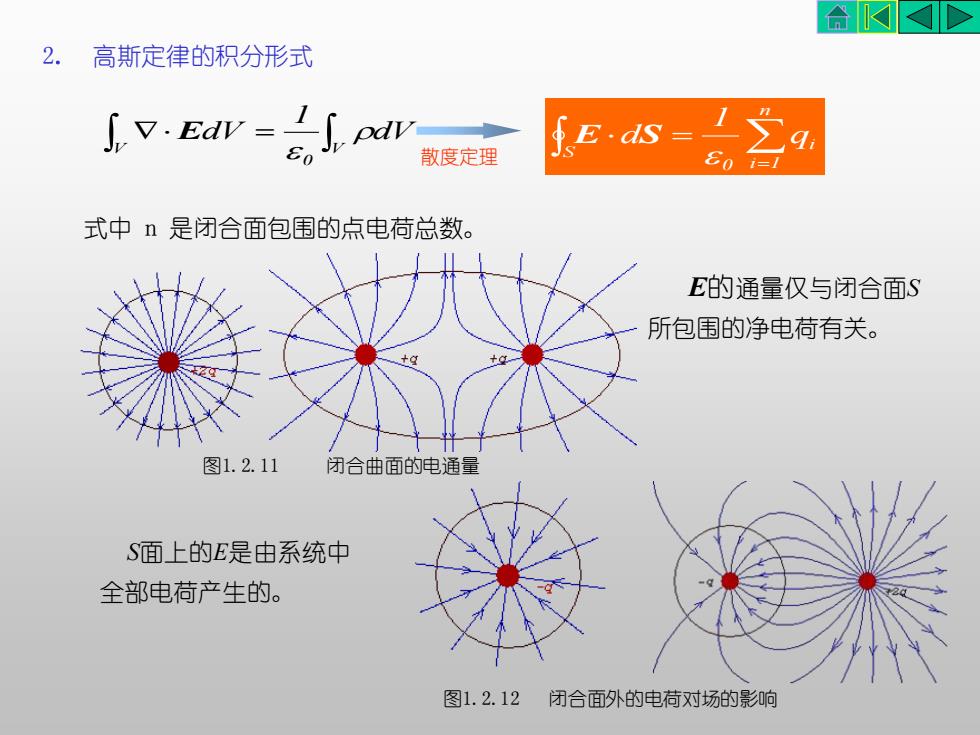
2. 高斯定律的积分形式 式中 n 是闭合面包围的点电荷总数。 = V V 0 dV 1 dV E = = n i 1 i 0 S q 1 d E S 散度定理 图1.2.11 闭合曲面的电通量 E的通量仅与闭合面S 所包围的净电荷有关。 图1.2.12 闭合面外的电荷对场的影响 S面上的E是由系统中 全部电荷产生的

合KKD1.2.3.电介质中的高斯定律1..静电场中导体的性质导体内电场强度E为零,静电平衡;导体是等位体,导体表面为等位面:电场强度垂直于导体表面;O电荷分布在导体表面,且 E=60图1.2.13静电场中的导体中思考+。接地导体都不带电。(X一导体的电位为零,则该导体不带电。,任何导体,只要它们带电量不变,则其电位是不变的。2.静电场中的电介质
• 电场强度垂直于导体表面; • 导体是等位体,导体表面为等位面; • 导体内电场强度E为零,静电平衡; 电荷分布在导体表面,且 。 0 E • = • 任何导体,只要它们带电量不变,则其电位是不变的。 ( ) • 一导体的电位为零,则该导体不带电。 ( ) • 接地导体都不带电。( ) 1.2.3. 电介质中的高斯定律 1. 静电场中导体的性质 2. 静电场中的电介质 图1.2.13 静电场中的导体

AKDE无极性分子有极性分子图1.2.14电介质的极化电介质在外电场E作用下发生极化,形成有向排列的电偶极矩;电介质内部和表面产生极化电荷;极化电荷与自由电荷都是产生电场的源。用极化强度P表示电介质的极化程度,即PP=limC/m2电偶极矩体密度AVAV0式中√p为体积元△V内电偶极矩的矢量和,P的方向从负极化电荷指向正极化电荷
• 电介质在外电场E作用下发生极化,形成有向排列的电偶极矩; • 电介质内部和表面产生极化电荷; • 极化电荷与自由电荷都是产生电场的源。 式中 为体积元 内电偶极矩的矢量和,P的方向从负极化电荷指向 正极化电荷。 p V 无极性分子 有极性分子 图1.2.14 电介质的极化 用极化强度P表示电介质的极化程度,即 V 0 V → = p P lim C/m2 电偶极矩体密度