
合KD3)E与?的微分关系E=-VP在静电场中,任意一点的电场强度E的方向总是沿着电位减少的最快方向,其大小等于电位的最大变化率。apapap在直角坐标系中:E=e.e.+ey+axayOz思考根据E与的微分关系,i试问静电场中的某一点X?=0→>E=0CDX(E=0→0=0?E.dl =-V.dl4)E与?的积分关系 dx+ dy+ap-dzl=-dg一E线OxayOz[P dp=(p)-(po)= fPE.dl参考点E.dl设Po为参考点(P(p)=图1.2.1E与的积分关系
3) E与 的微分关系 E = − 在静电场中,任意一点的电场强度E的方向总是沿着电位减少的最快 方向,其大小等于电位的最大变化率。 在直角坐标系中: [ ] x y z x y z E e e e + + = − • E = 0 → = 0 ? ( ) • = 0 → E = 0 ? ( ) 4) E与 的积分关系 E dl = − dl − = − = 0 p0 p 0 p p d ( p ) ( p ) E dl dz d z dy y dx x = − + + = −[ ] 设P0为参考点 = 参考点 p ( p) E dl 根据 E 与 的微分关系,试问静电场中的某一点 图1.2.1 E与 的积分关系

AKKD5)电位参考点的选择原则场中任意两点的电位差与参考点无关。同一个物理问题,只能选取一个参考点。选择参考点尽可能使电位表达式比较简单,且要有意义。q例如:点电荷产生的电场:+C?4元80Pl r=o = 0C>8表达式无意义qPlr→ = 0C=04元80r9qqC=:lr=R = 04元6R4元80r4元R电荷分布在有限区域时,选择无穷远处为参考点;电荷分布在无穷远区时,选择有限远处为参考点
5) 电位参考点的选择原则 • 场中任意两点的电位差与参考点无关。 • 同一个物理问题,只能选取一个参考点。 • 选择参考点尽可能使电位表达式比较简单,且要有意义。 例如:点电荷产生的电场: C 4 r q 0 = + r=0 = 0 C → r→ = 0 4 r q 0 = C = 0 表达式无意义 r=R = 0 4 R q 4 r q 0 0 = − 4 R q C 0 = − • 电荷分布在有限区域时,选择无穷远处为参考点; • 电荷分布在无穷远区时,选择有限远处为参考点

合KKD6)电力线与等位线(面)。E线:曲线上每一点切线方向应与该点电场强度的方向一致,若dl是电力线的长度元,E矢量将与dl方向一致,故电力线微分方程E×dl=0E-E,_E.在直角坐标系中:微分方程的解即为电力线E的方程。dxdydz等位线(面)方程:·在静电场中电位相等的点的曲面称为等位面,即p(x, y,z)=C当取不同的C值时,可得到不同的等位线(面)。画出电偶极子的等位线和电力线(r>>d)。例1.2.1
6) 电力线与等位线(面) • E 线:曲线上每一点切线方向应与该点电场强度E的方向一致,若 是电力线的 长度元,E 矢量将与 dl 方向一致, dl Edl = 0 故电力线微分方程 dz E dy E dx Ex y z 在直角坐标系中: = = 微分方程的解即为电力线 E 的方程。 当取不同的 C 值时,可得到不同的等位线(面)。 • 在静电场中电位相等的点的曲面称为等位面,即 ( x, y,z ) = C 等位线(面)方程: 例1.2.1 画出电偶极子的等位线和电力线(r d)

AKDz在球坐标系中:p(p0.0)11qqr-n才Pp=+qR4元4元02r2r2eR1d?d?r =(r+r =(r2 +srd cos0)2,+rdcos0)44-q图1.2.2电偶极子用二项式展开,又有r>>d,得等位线方程(球坐标系):+.cosodr=r-s5=r+9-cosO22pcoser=C"Ncoso=C,4元8r?代入上式,得qdcose电力线微分方程(球坐标系):p·erPp=s4元802—4元80dr_rdoE,-E。P表示电偶极矩,方向由负电荷指向正电荷。将E。和E代入上式,q4ns,r(2cos Ce, + sin ea)E,=-V0:解得E线方程为r=Dsine
在球坐标系中: 1 2 2 1 0 1 2 0 p r r r r 4 q ) r 1 r 1 ( 4 q − = − = 2 0 r 2 0 p 4 r 4 r qd cos pe = = ( 2cos sin ) 4 r q 3 r 0 p E = − = e + e E rd E dr r = 电力线微分方程(球坐标系): 2 2 1 2 2 2 2 1 2 1 rd cos ) 4 d rd cos ) r (r 4 d r = (r + − , = + + 代入上式,得 r = Dsin 解得E线方程为 将 E 和 Er 代入上式, 等位线方程(球坐标系): C, r = C' cos r p = 2 4 0 cos cos 2 d r r 2 = + 用二项式展开,又有 r d ,得 cos 2 d r r 1 = − p 表示电偶极矩,方向由负电荷指向正电荷。 图1.2.2 电偶极子 r1 r2
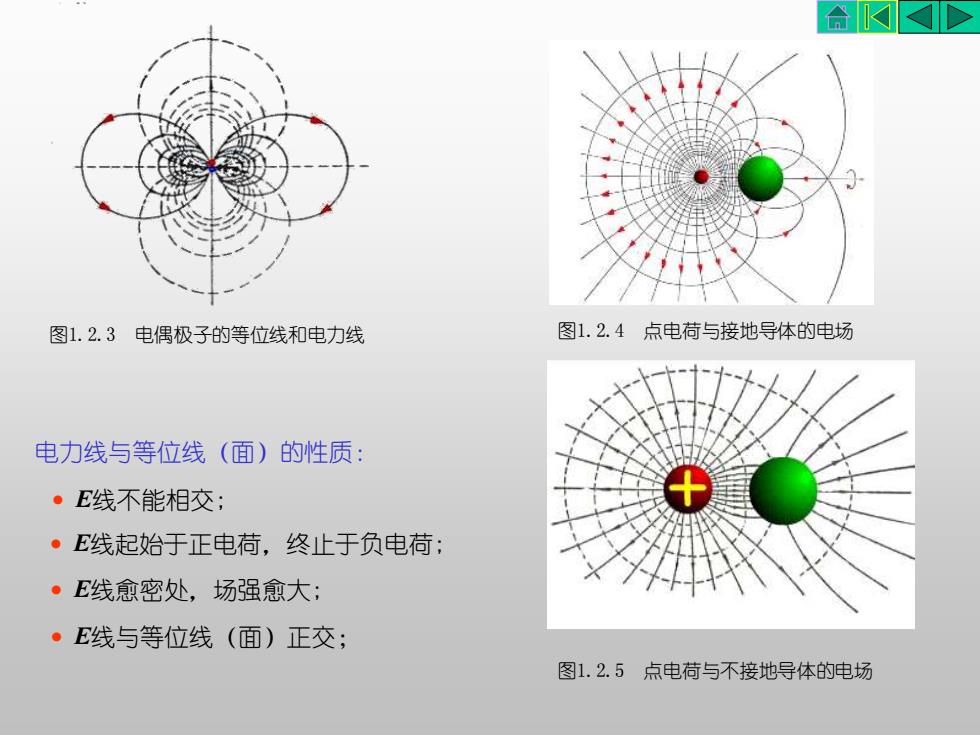
合K图1.2.4点电荷与接地导体的电场图1.2.3电偶极子的等位线和电力线电力线与等位线(面)的性质:·E线不能相交:·E线起始于正电荷,终止于负电荷:·E线愈密处,场强愈大;·E线与等位线(面)正交;图1.2.5点电荷与不接地导体的电场
电力线与等位线(面)的性质: • E线不能相交; • E线起始于正电荷,终止于负电荷; • E线愈密处,场强愈大; • E线与等位线(面)正交; 图1.2.3 电偶极子的等位线和电力线 图1.2.4 点电荷与接地导体的电场 图1.2.5 点电荷与不接地导体的电场