AKKD例1.1.1真空中有长为L的均匀带电直导线,电荷线密度为丁,试求P点的电场解:采用直角坐标系,令y轴经过场点p,导线与x轴重合。tdxadE,dE(x, y) :4元8(x+y)UxdEdEdxX0X-上Vx+-L,L.ydEdE.X2+图1.1.4带电长直导线的电场11Tx2EL4元(x+)4元8Vx?+L+JL,+y2L,L,yE4元8(+)4元80+V+V当L=L+L,>8时,10(直角坐标)E,(y)=E,e, +Ele2元80TE(p,d,z)=E.e。+E(圆柱坐标)2元60P
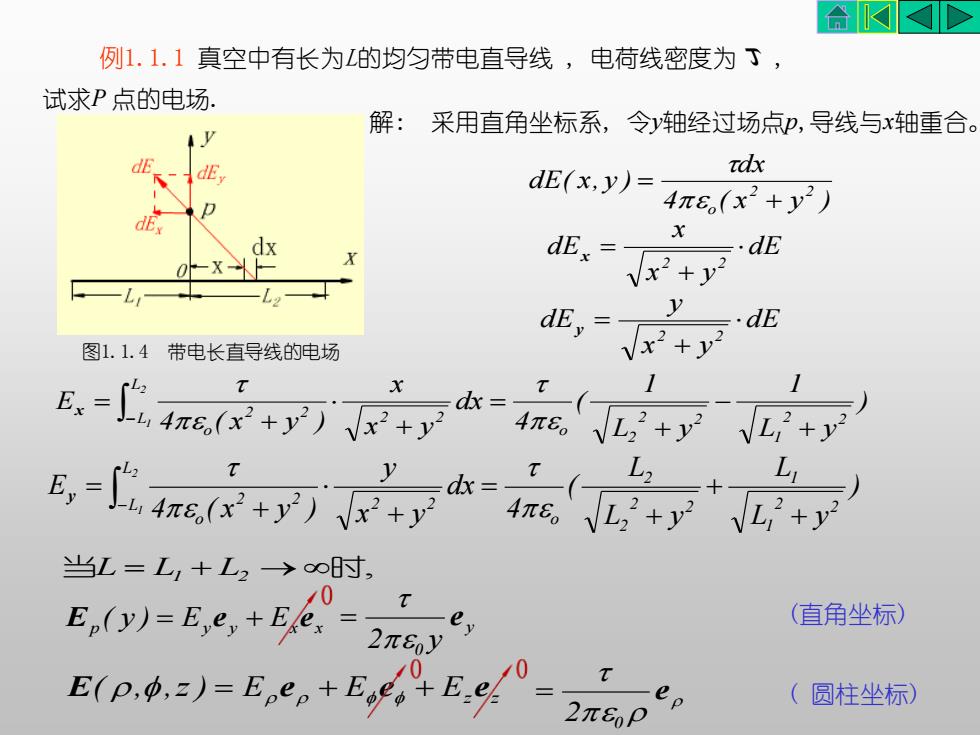
例1.1.1 真空中有长为L的均匀带电直导线 , 电荷线密度为 , 试求P 点的电场. 解: 采用直角坐标系, 令y轴经过场点p,导线与x轴重合。 4 ( x y ) dx dE( x, y ) 2 2 o + = dE x y x dE 2 2 + x = dE x y y dE 2 2 + y = ) L y 1 L y 1 ( 4 dx x y x 4 ( x y ) E 2 2 1 2 2 2 o 2 2 L L 2 2 o 2 1 + − + = + + = − x ) L y L L y L ( 4 dx x y y 4 ( x y ) E 2 2 1 1 2 2 2 2 o 2 2 L L 2 2 o 2 1 + + + = + + = − y 当 = + →时, L L1 L2 p Ey y Ex x E ( y ) = e + e (直角坐标) y 0 2 y e = E E Ez z E( , ,z ) = e + e + e ( 圆柱坐标) e 2 0 = 图1.1.4 带电长直导线的电场

合KKD讨论与引伸无限长直均匀带电导线产生的电场为平行平面场。电场强度E(x,y,z)的矢量积分一般先转化为标量积分,然后再合成,即E=Eex+Ee+Ee·积分是对源点(x,y",z)进行的,计算结果是场点(x,y,z)的函数。点电荷的数学模型点电荷是电荷体分布的极限情况,可以把它看成是一个体积很小,电荷密度很大,总电量不变的带电小球体。当α一0时,电荷密度趋近于无穷大,通常IZ用冲击函数s表示点电荷的密度分布。N(xy.z)r0当r0S(x,y,z)=(r)=8当r=009.. S(x, y,z)dV'= (..8(r )dV'= 1(积分区域V包含r=0点)图1.1.5单位点电荷的密度分布点电荷的密度p(r)=q(r)
• 无限长直均匀带电导线产生的电场为平行平面场。 • 电场强度 E( x, y,z ) 的矢量积分一般先转化为标量积分, 然后再合成,即 E = Ex ex + Ey ey + Ez ez • 点电荷的数学模型 • 积分是对源点 (x' , y' ,z') 进行的,计算结果是场点 (x, y,z) 的函数。 点电荷是电荷体分布的极限情况,可以把它看成是一个体积很小,电荷密度 很大,总电量不变的带电小球体。 当 时,电荷密度趋近于无穷大,通常 用冲击函数 表示点电荷的密度分布。 a →0 ( x, y,z ) = (r ) = 当r 0 当r = 0 0 ( x, y,z)dV' (r)dV' 1 V' V' = = (积分区域V'包含r =0点) 图1.1.5 单位点电荷的密度分布 点电荷的密度 (r ) = q(r )

AKKD1.2静电场环路定律和高斯定律1.2.1静电场环路定律1.静电场旋度a点电荷E(r)=4元80[r-rr-rq_xV×E(r)=r-r134元80V×CF=CV×F+VCxF量恒等式r-r'1Vx-Vx(r-r)+vr-rr-r-rVx(r-r')=0直接微分得1x(r-r)=-3r-)Ax(r-r)=0r-rr-rl故V×E()=0电场强度E的旋度等于零
点 电 荷 3 0 ' ' 4 q ( ) r r r r E r − − = 3 0 ' ' 4 q ( ) r r r r E r − − = 矢量恒等式 CF =CF +CF ( ' ) ' 1 ( ' ) ' 1 ' ' 3 3 3 r r r r r r r r r r r r − − − + − = − − 直接微分得 (r − r' ) = 0 ( ' ) 0 ' ' ( ' ) 3 ' 1 3 3 − = − − − = − − r r r r r r r r r r 故 E(r ) 0 电场强度E 的旋度等于零 1.2 静电场环路定律和高斯定律 1. 静电场旋度 1.2.1 静电场环路定律

合KKD可以证明,上述结论适用于点电荷群和连续分布电荷产生的电场。即任一分布形式的静电荷产生的电场的旋度恒等于零,即VxE=-0表明静电场是一个无旋场2.静电场的环路定律由斯托克斯定理,得E.dl=9(V×E)·ds=0在静电场中,电场强度沿着闭合回路的环量恒等于零。。电场力作功与路径无关,静电场是保守场E·dl=0二者等价。V×E=0无旋场一定是保守场,保守场一定是无旋场
• 可以证明,上述结论适用于点电荷群和连续分布电荷产生的电场。 表明 静电场是一个无旋场。 即任一分布形式的静电荷产生的电场的旋度恒等于零,即 E = 0 2. 静电场的环路定律 • 在静电场中,电场强度沿着闭合回路的环量恒等于零。 • 电场力作功与路径无关,静电场是保守场。 无旋场一定是保守场,保守场一定是无旋场。 = l s E dl ( E ) ds 0 由斯托克斯定理,得 • = = l E 0 E dl 0 二者等价

AKD3电位函数1)电位的引出:V×E=0,根据量恒等式×Vβ=0E=-V在静电场中可通过求解电位函数(Potential),再利用上式可方便地求得电场强度E。式中负号表示电场强度的方向从高电位指向低电位。2)已知电荷分布,求电位以点电荷为例推导电位qr-r点电荷群E(r)= -4元%r-1qip(r):+4元%=-1r-r'r-rlIr-rl连续分布电荷q:. E(r)=-V1dq-Vpr)p(r)=O4元r-r4元8r-rq. p(r)=+Ctdldq: pdV, odS,4元r-
3 . 电位函数 E = − 在静电场中可通过求解电位函数(Potential), 再利用上式可方便地求得 电场强度E 。式中负号表示电场强度的方向从高电位指向低电位。 2) 已知电荷分布,求电位: 3 0 ' ' 4 q ( ) r r r r E r − − = C ' q 4 1 (r ) N i 1 i i 0 + − = = r r 点电荷群 C ' dq 4 1 (r ) v' 0 + − = r r 连续分布电荷 1) 电位的引出 以点电荷为例推导电位: 3 ' ' ' 1 r r r r r r − − = − − (r ) 4 ' q ( ) 0 = − − = − r r E r C 4 ' q (r ) 0 + − = r r E = 0, 根据矢量恒等式 = 0 dq : dV , dS, dl