
(六)、基本初等函数与初等函数 1、基本初等函数 1)、幂函数y=x。 2)、指数函数y=a。 3)、对数函数y=Logx。 4)、三角函数y=sinx.y=cosx,y=tanx.y=cot.=s0cxy=cscx· 5)、反三角函数y=arcsinx,y=arecosx,.y=arctanx,.y=arccotx。 一一了解基本性质与图形,掌握变换公式。 2、初等函数(17页) 由基本初等函数与常数经过有限次四则运算和复合运算组成能用一 个式子 来表示的函数,称为初等函数 3、双曲函数与反双曲函数 1)、双曲函数 y=sh=e'-e y=ch=e'te 2 加 2)、反双曲函数(略) 6
6 (六)、基本初等函数与初等函数 1、 基本初等函数 1)、幂函数 n y x = 。 2)、指数函数 x y a = 。 3)、对数函数 a y Log x = 。 4)、三角函数 y x y x y x y x y x y x = = = = = = sin , cos , tan , cot , sec , csc . 。 5)、反三角函数 y x y x y x y arc x = = = = arcsin , arccos , arctan , cot 。 -了解基本性质与图形,掌握变换公式。 2 、初等函数(17 页) 由基本初等函数与常数经过有限次四则运算和复合运算组成能用一 个式子 来表示的函数,称为初等函数 3、 双曲函数与反双曲函数 1)、双曲函数 2 2 x x x x x x x x e e y shx e e y chx e e y thx e e − − − − − = = + = = − = = + 2)、反双曲函数(略)
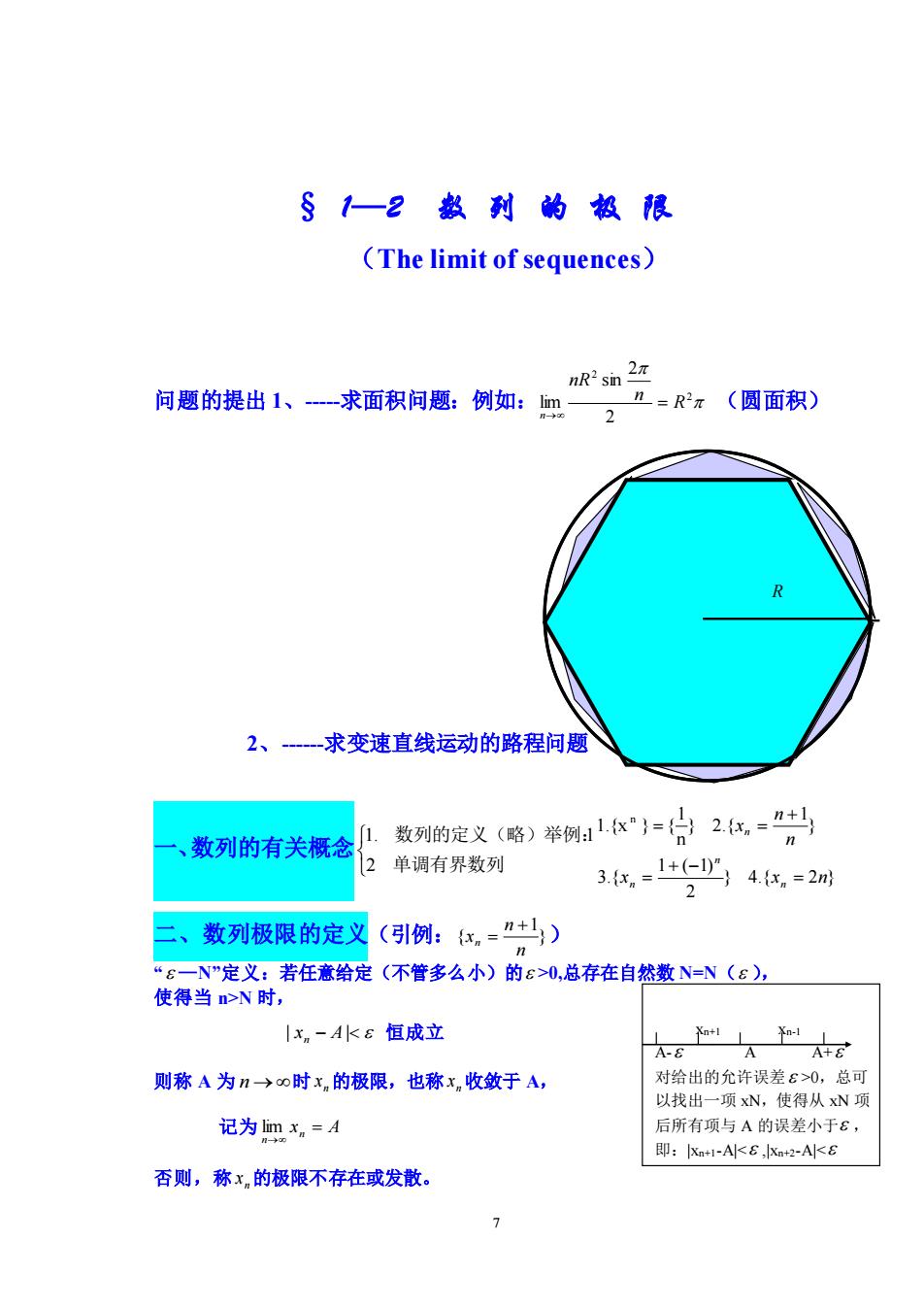
§1一2数到的极限 (The limit of sequences) 向题的提出、一求面积问题:例如:m如 2”=x(圆面积) 2、-求变速直线运动的路程问题 、数列的有关概念 数列的定义(略)举例11x=白2任,="+马 2 单调有界数列 3.x,=1+少4,=2 2 二、数列极限的定义(引例:化,-”+马) “8一N”定义:若任意给定(不管多么小)的s>0,总存在自然数N=N(ε)。 使得当n>N时, x。-AK6恒成立 和1La1 A-8 A 则称A为n→∞时x的极限,也称x收敛于A, 对给出的允许误差£>0,总可 以找出一项xN,使得从xN项 记为imx,=A 后所有项与A的误差小于6, 即:K1-AE,K2-AKE 否则,称x,的极限不存在或发散。 7
7 § 1—2 数 列 的 极 限 (The limit of sequences) 问题的提出 1、-求面积问题:例如: 2 2 2 2 sin lim R n nR n = → (圆面积) 2、-求变速直线运动的路程问题 一、数列的有关概念 单调有界数列 数列的定义(略)举例: 2 1. 1 } 4.{ 2 } 2 1 ( 1) 3.{ } 1 } 2.{ n 1 1.{x } { n x x n n n x n n n n = + − = + = = 二、数列极限的定义(引例: } 1 { n n xn + = ) “ —N”定义:若任意给定(不管多么小)的 >0,总存在自然数 N=N( ), 使得当 n>N 时, | x − A | n 恒成立 则称 A 为 n → 时 n x 的极限,也称 n x 收敛于 A, 记为 xn A n = → lim 否则,称 n x 的极限不存在或发散。 xn+1 xn-1 A- A A+ 对给出的允许误差 >0,总可 以找出一项 xN,使得从 xN 项 后所有项与 A 的误差小于 , 即:|xn+1-A|< ,|xn+2-A|< R R

注意理解几点: 1)(任意性)s是任意给定的正数,只有这样才能刻画x,→A 的极限本质。 2)(不唯一性)只要对于给定的ε,能找到一个N便可。 3)(相关性)N与ε有关,不同的ε有不同的N,但不存在 函数关系。一般地,若ε减少,则N增大。 4)求N的方法与原则: 直接法—一x。-Ak出发。解一个关于n的不等式。一 般可以得出n>(e)的形式。则N=[p(e】为所求。 放大法—把x,-A放大后变为B),然后解Bm<E 举例:)名台行以宁训k时电=0如品2 (放大法、直接法) (三)几个结论: X收敛之x有界,(证明》 1、(有界性:X无界会X,发散 例如:X。=((-1)° 2、(唯一性):若1mxn=A且mxn=B,则A=B 即:若X收敛,则其极限唯一
8 注意理解几点: 1) (任意性) 是任意给定的正数,只有这样才能刻画 xn → A 的极限本质。 2) (不唯一性)只要对于给定的 ,能找到一个 N 便可。 3) (相关性)N 与 有关,不同的 有不同的 N,但不存在 函数关系。一般地,若 减少,则 N 增大。 4) 求 N 的方法与原则: 直接法——| x − A | n 出发。解一个关于 n 的不等式。一 般可以得出 n ( ) 的形式。则 N = [( )] 为所求。 放大法——把 | x A| n − 放大后变为 (n),然后解(n) 举例: 2 1 2 3) | | 1 lim 0 4)lim 2 1 2) ( 1) ( 1) 1) 2 1 = + = = + − = → → + n n x q q n x n n n n n n n 时, (放大法、直接法) (三) 几个结论: 1、(有界性): ( 1) n n n n n n X X X X X ⎯⎯⎯ ⎯⎯⎯→ ⎯⎯⎯ ⎯⎯⎯→ = − 一定 不一定 一定 不一定 收敛 有界,(证明) 无界 发散 例如: 2、(唯一性):若 lim xn = A,且lim xn = B,则A = B 即:若 X n收敛,则其极限唯一

了、(保号性):若mX,=A且4>0(或1<0,则存在自然数,当>N时 X。>0(或X<0). 若存在自然数N,当n>N时xn之0,(Xn≤0),且limX。=A, 则A≥0(A≤0). 4、(母、子统一性):(祥见P30-Th4) 收敛数列的子数列也收敛,且极限值相同。 例子:设mx,=a+l,且已知mx,=3,则a=2 §1一3离数的极限 (The limit of function) (一)、函数极限的定义(以x极限的定义引入) 定义 存在到 当x变化恒有(关 结论 记号 系成立) A 为 £-δ定义 δ<00<x-xl<6IfAK8 (P32D) x→x时(x)的极限。 lim f(x)=4 6>0 “6-定义“ x>X 4为当r→o时f(x)的极限。 lim f(x)=A X>0 f(x)-AKE (P35-D) 9
9 3、(保号性): lim , 0( 0), 0( 0). n n X A A A → = n n 若 且 或 则存在自然数N,当n>N时 X 或X , 0,( 0), lim , 0( 0). n n n n N n N X X X A A A → = 若存在自然数 当 时 且 则 4、(母、子统一性):(祥见 . P Th 30 4 −−− ) 收敛数列的子数列也收敛,且极限值相同。 例子:设 lim = +1 lim = 3 = 2 → → x a xn a n n n ,且已知 ,则 §1—3 函 数 的 极 限 (The limit of function) (一) 、函数极限的定义(以 xn极限的定义引入) 定义 任 给 存在 当 x 变化 到 恒有(关 系成立) 结论 记号 − 定义 (P32-D-1) >0 <0 0 0 − x x |f(x)-A|< A 为 当 x x f x → 0时 ( )的极限。 ( ) 0 lim x x f x A → = “ − X定义“ (P35-D-1) >0 x X |f(x)-A|< A x f x 为当 → 时 ( )的极限。 f x A x = → lim ( )