
第二节定积分的几何应用 一、平面图形的面积 1直角坐标系 作为一般情况讨论,设平面图形由【,b] 上连续的两条曲线y=f(x)与y=g(x) (f(x)≥g(x)及两条直线x=Mx=b所围成 在[a,b】上任取典型小区间[x+dk] 与它相对应的小曲边梯形的面积为局部量A
第二节 定积分的几何应用 一、平面图形的面积 1 直角坐标系 作为一般情况讨论,设平面图形由 [ a , b ] 上连续的两条曲线 y = f ( x ) 与 y = g ( x ) ( f (x) g(x)) 及两条直线 x =a ,x =b 所围成 在 [a ,b ] 上任取典型小区间[ x ,x+dx ] 与它相对应的小曲边梯形的面积为局部量dA
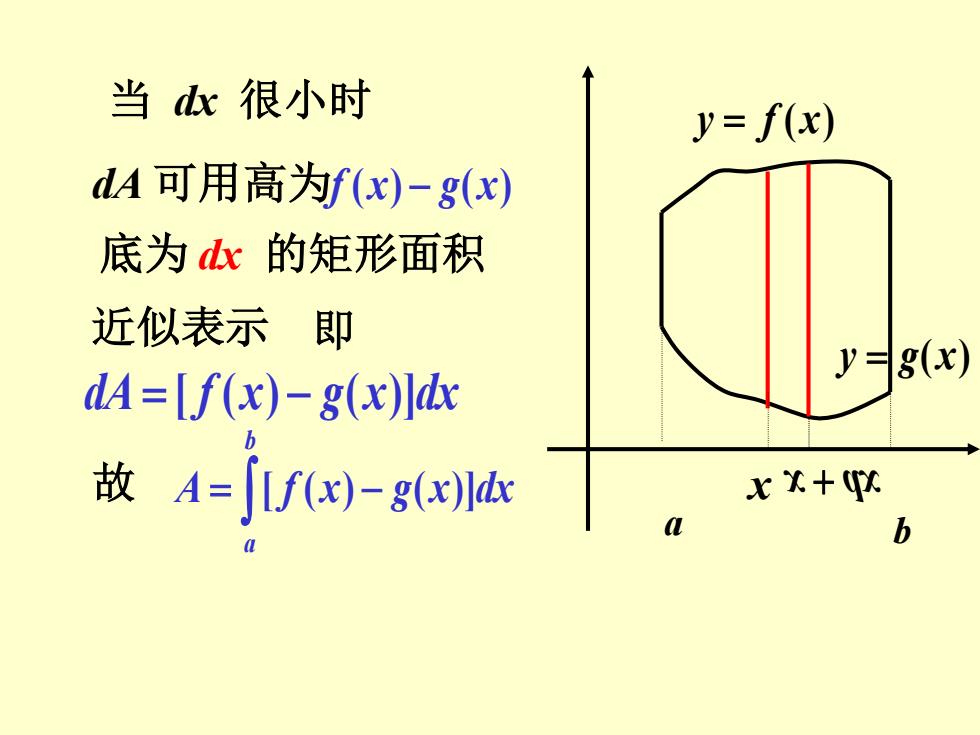
当dx很小时 y=f(x) dA可用高为f(x)-g(x) 底为dx的矩形面积 近似表示即 y=g(x) dA=If(x)-g(x)ldx 故仁j-gM xx+(px b
dA 可用高为 f (x) − g(x) 底为 dx 的矩形面积 近似表示 即 dA = [ f (x) − g(x)]dx 故 = − b a A [ f (x) g(x)]dx a b y = f (x) y = g(x) x x + dx 当 dx 很小时

2 例1求两曲线 y= 2+1 y=x2 所围成的图形的面积 解为确定图形的存在区间 由联立方程组解得交点A(-1,1)B(1,1) xe-1,1川 、2 ≥2 ,2 x2+1 故A= ,x2+1 -x2) =(2 arcta.x-H=元-子 3
1 2 2 + = x y 2 y = x 所围成的图形的面积 解 为确定图形的存在区间 由联立方程组解得交点 A(-1,1) B(1,1) x [−1,1] 2 2 1 2 x x + 故 − − + = 1 1 2 2 ) 1 2 ( x dx x A 1 1 3 ) 3 1 = (2arctan − − x x 3 2 = − 例1 求两曲线

例2计算y2=2xy=x-4所围图形的面积 解首先定出图形所在的范围 y2=2x解得交点为(2,2)和(8,4) y=x-4 若取x为积分变量在比,x+x上取部分量 则对于x的不同值局部量的位置不同其 上、下曲边有多种情况运用上述公式计算 较为复杂 如下图
y 2x 2 = y = x − 4 所围图形的面积 解 首先定出图形所在的范围 y x y x 2 4 2 = = − 解得交点为(2,-2)和(8,4) 若取 x 为积分变量 在 [x,x+dx] 上取部分量 则对于 x 的不同值局部量的位置不同 其 上、下曲边有多种情况运用上述公式计算 较为复杂 如下图 例2 计算

但若将这一面积看作是分布在区间[-2,4上 以y为变量计算将会简单 在-2,4上任取一小区间y,y+ 其上相应的窄条左、右曲边分别为 =2,x=y+4 →A=U+4-2=18
以 y 为变量计算将会简单 在[-2,4] 上任取一小区间 [ y, y + dy] 其上相应的窄条左、右曲边分别为 , 4 2 1 2 x = y x = y + ) 18 2 1 ( 4 2 4 2 = + − = − A y y dy 但若将这一面积看作是分布在区间 [ -2,4] 上