
《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组
1 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

图论 一、学习目的与要求 图论是近年来发展迅速而又应用广泛的一门学科。本章主要讲授 图论的基本概念和定理,重点是欧拉图与汉密尔顿图、平面图、树。 要求熟练掌握图的基本概念和定理并能够进行简单应用。 二、知识点 1图的基本概念: 2链(或路)与圈(或回路): 3图的矩阵表示: 4欧拉图与汉密尔顿图 5平面图: 6对偶图与着色 7树与生成树: 8根树及其应用。 三、要求 1.识记 图和树相关的数据结构、算法和计数 2.领会 图的有关概念和表示以及计算中使用图和树构建的模型。 四、主要内容 图论 7-1图的基本概念 什么是图?可用一句话概括,即:图是用点和线来刻划离散事物集 合中的每对事物间以某种方式相联系的数学模型。因为它显得太抽象, 不便于理解,所以有必要给出另外的回答。下面便是把图作为代数结 构的一个定义。 一、图的定义 1、图的定义 定义7-1.1:一个图是一个三元组<W(G),E(G),9c>,其中V(G)={v1 v2.,vn为有限非空结点集合,V1称为结点,E(G)={e1,.,e 为有限的边集合,©:称为边,pc是从边集合E到结点对集合上的函数。 图可简记为:G=<W,E>。 例1:G=<W(G),E(G),9c 2
2 图论 一、学习目的与要求 图论是近年来发展迅速而又应用广泛的一门学科。本章主要讲授 图论的基本概念和定理,重点是欧拉图与汉密尔顿图、平面图、树。 要求熟练掌握图的基本概念和定理并能够进行简单应用。 二、知识点 1 图的基本概念; 2 链(或路)与圈(或回路); 3 图的矩阵表示; 4 欧拉图与汉密尔顿图 5 平面图; 6 对偶图与着色; 7 树与生成树; 8 根树及其应用。 三、要求 1.识记 图和树相关的数据结构、算法和计数 2.领会 图的有关概念和表示以及计算中使用图和树构建的模型。 四、主要内容 图论 7-1 图的基本概念 什么是图?可用一句话概括,即:图是用点和线来刻划离散事物集 合中的每对事物间以某种方式相联系的数学模型。因为它显得太抽象, 不便于理解,所以有必要给出另外的回答。下面便是把图作为代数结 构的一个定义。 一、图的定义 1、图的定义 定义 7-1.1:一个图是一个三元组<V(G),E(G), G >,其中 V(G)={v1, v 2,.,v n }为有限非空结点集合,v i 称为结点,E(G)={e1,.,e m } 为有限的边集合,e i 称为边, G 是从边集合 E 到结点对集合上的函数。 图可简记为:G=<V,E>。 例 1:G=<V(G),E(G), G >
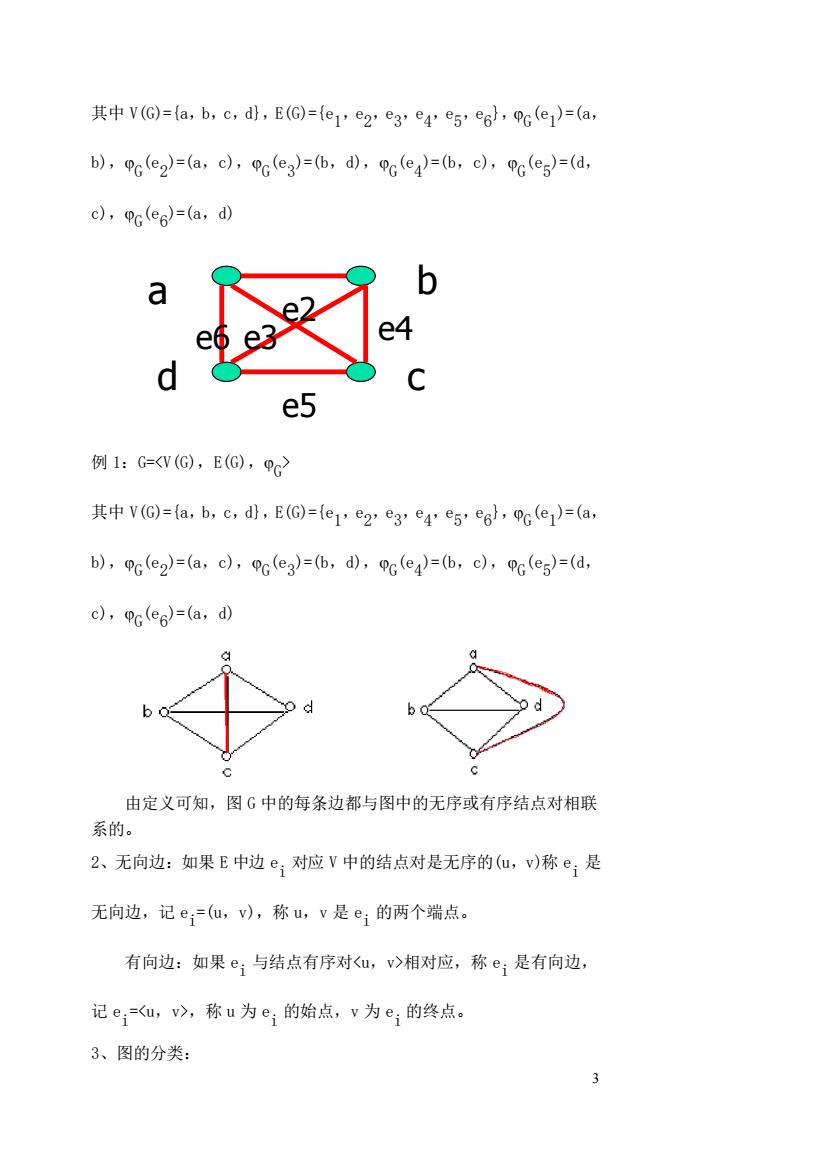
V(G)=(a,b,c,d),E(G)=(e,e2.eg,e es,es),G(e)=(a, b),PG(e2)=(a,c),G(e3)=(b,d),(e)=(b,c),(es)=(d, c),G(es)=(a,d) a b e5 例1:G=<W(G),E(G),9c2 其中vG=a,b,c,d,E(G)={e1e2e3e4e5eg,96e1=a, b),(e2)=(a,c),G(e2)=(b,d),(e)=(b,c),G(es)=(d, c),c(es)=(a,d) 由定义可知,图G中的每条边都与图中的无序或有序结点对相联 系的。 2、无向边:如果E中边e:对应V中的结点对是无序的(u,v)称e:是 无向边,记e:=(u,v),称u,v是e:的两个端点。 有向边:如果e;与结点有序对<u,v>相对应,称e:是有向边, 记e:=u,v>,称u为e;的始点,v为e:的终点。 3、图的分类:
3 其中 V(G)={a,b,c,d},E(G)={e1 ,e 2 ,e 3 ,e 4 ,e 5 ,e 6 }, G (e1 )=(a, b), G (e2 )=(a,c), G (e3 )=(b,d), G (e4 )=(b,c), G (e5 )=(d, c), G (e6 )=(a,d) 例 1:G=<V(G),E(G), G > 其中 V(G)={a,b,c,d},E(G)={e1 ,e 2 ,e 3 ,e 4 ,e 5 ,e 6 }, G (e1 )=(a, b), G (e2 )=(a,c), G (e3 )=(b,d), G (e4 )=(b,c), G (e5 )=(d, c), G (e6 )=(a,d) 由定义可知,图 G 中的每条边都与图中的无序或有序结点对相联 系的。 2、无向边:如果 E 中边 e i 对应 V 中的结点对是无序的(u,v)称 e i 是 无向边,记 e i =(u,v),称 u,v 是 e i 的两个端点。 有向边:如果 e i 与结点有序对<u,v>相对应,称 e i 是有向边, 记 e i =<u,v>,称 u 为 e i 的始点,v 为 e i 的终点。 3、图的分类: a b d c e2 e3 e4 e5 e6

①无向图:每条边均为无向边的图称为无向图。 ②有向图:每条边均为有向边的图称为有向图。 ③混合图:有些边是无向边,有些边是有向边的图称为混合图。 见273页图7-1.2 (a)是无向图 (6)是有向图 (c)是混合图 练习:画出下面的图 (1)G1=<W1,E1>是无向图,其中V1=W1,V2,V3,V4,V5,V6, E1={el,e2,e3,e4,e5,e6, e1=(W1,V3),e2=(W1,V4),e2=(W2,V4),e3=(W3,V4),e4=(W3, V6),e5=(W4,V5),e6=(W5,V6) (2)G2=<W2,E2>是有向图,其中V2=(V1,V2,V3,V4},E={<W3, V1,<W3,V2>,<W1,V1>,<W1,V2>, <W4,V1>,<V3,V4>,<W4,V3>} (3)G3=<W3,e3>是混合图,V3=W1,V2,V3,V4, E3={<W1,V1>,(W1,V3),<W3,V1>,<W1,V2>,(W4,V2)} 4、点和边的关联:如e:=(u,v)或e=<u,v>称u,v与e1关联 5、点与点的相邻:关联于同一条边的结点称为邻接点。 6、边与边的邻接:关联于同一结点的边称为邻接边。 7、孤立结点:不与任何结点相邻接的结点称为孤立结点。 8、零图:仅有孤立结点的图。 9、平凡图:仅有一个孤立结点的图。 10、自回路(环):关联于同一结点的边称为自回路,或称为环。见274 页图7-1.3(c,c)是环 11、平行边:在有向图中,始点和终点均相同的边称为平行边,无向 图中若两点间有多条边,称这些边为平行边,两点间平行边的条数称 为边的重数。 二、点的度数 1、点的度数的定义 定义7-1.2:在图G=<V,E>,v∈V,与结点v关联的边数称为该点的度 数,记为deg(w)。孤立结点的度数为0。 2、出度与入度 定义T-1.3:在有向图中,veV,以v为始点的边数称为该结点的出度, 记作deg(v):以v为终点的边数称为该结点的入度,记作deg(w)。 显然有deg(w)=deg(v)+deg(w) 4
4 ①无向图:每条边均为无向边的图称为无向图。 ②有向图:每条边均为有向边的图称为有向图。 ③混合图:有些边是无向边,有些边是有向边的图称为混合图。 见 273 页图 7-1.2 (a)是无向图 (b)是有向图 (c)是混合图 练习:画出下面的图。 (1)G1=<V1,E1>是无向图,其中 V1={V1,V2,V3,V4,V5,V6}, E1={e1,e2,e3,e4,e5,e6}, e1=(V1,V3),e2=(V1,V4),e2=(V2,V4),e3=(V3,V4),e4=(V3, V6),e5=(V4,V5),e6=(V5,V6) (2)G2=<V2,E2>是有向图,其中 V2={V1,V2,V3,V4},E={<V3, V1>,<V3,V2>,<V1,V1>,<V1,V2>, <V4,V1>,<V3,V4>,<V4,V3>} (3)G3=<V3,e3>是混合图,V3={V1,V2,V3,V4}, E3={<V1,V1>,(V1,V3),<V3,V1>,<V1,V2>,(V4,V2)} 4、点和边的关联:如 e i =(u,v)或 e i =<u,v>称 u,v 与 e i 关联。 5、点与点的相邻:关联于同一条边的结点称为邻接点。 6、边与边的邻接:关联于同一结点的边称为邻接边。 7、孤立结点:不与任何结点相邻接的结点称为孤立结点。 8、零图:仅有孤立结点的图。 9、平凡图:仅有一个孤立结点的图。 10、自回路(环):关联于同一结点的边称为自回路,或称为环。见 274 页图 7-1.3 (c,c)是环 11、平行边:在有向图中,始点和终点均相同的边称为平行边,无向 图中若两点间有多条边,称这些边为平行边,两点间平行边的条数称 为边的重数。 二、点的度数 1、点的度数的定义 定义 7-1.2:在图 G=<V,E>,vV,与结点 v 关联的边数称为该点的度 数,记为 deg(v)。孤立结点的度数为 0。 2、出度与入度 定义 7-1.3:在有向图中,vV,以 v 为始点的边数称为该结点的出度, 记作 deg+ (v);以 v 为终点的边数称为该结点的入度,记作 deg- (v)。 显然有 deg(v)=deg+ (v)+deg- (v)

如:G1是无向图,deg(v1)=3,deg(v2)=1 G2是有向图,deg(w1)=3,deg(w1)=2,deg(v1)=5 v1 O -0v2 G1 v3 v4 G2 3、最大度和最小度: 图G最大度记为△(G)=max{deg(w)lveV(G)}, 最小度数记为8(G)=min{deg(w)lveV(G)}。 4、定理7-1.1:每个图中,结点度数总和等于边数的两倍。即 ∑deg(v)=2lEl 该定理又称握手定理 证明因为每条边必关联两个结点,而一条边给予关联的每个结点的 度数为1。因此在每个图中,结点度数总和等于边数的两倍。 5、定理7-1.2:在任何图中,度数为奇数的结点的个数必为偶数。 6、定理7-1.3:在任何有向图中,所有结点的入度之和等于所有结点 的出度之和。 证明因为每一条有向边必对应一个入度和一个出度,若一个结点具有 一个入度或出度,则必关联一条有向边,所以有向图中,各结点入度 之和等于边数,各结点出度之和也等于边数。因此,在任何有向图中, 所有结点的入度之和等于所有结点的出度之和。 三、特殊的图 1、多重图 定义7-1.4:含有平行边的图称为多重图。 2、简单图:不含平行边和环的图称为简单图。 3、完全图 定义7-1.5:简单图G=<V,E>中,若每一对结点间均有边相连,则称 该图为完全图。 5
5 如:G1 是无向图,deg(v1)=3,deg(v2)=1 G2 是有向图,deg+ (v1)=3,deg- (v1)=2,deg(v1)=5, 3、最大度和最小度: 图 G 最大度记为 (G)=max{deg(v)|vV(G)}, 最小度数记为 (G)=min{deg(v)|vV(G)}。 4、定理 7-1.1:每个图中,结点度数总和等于边数的两倍。即 deg(v)=2|E| 该定理又称握手定理 证明 因为每条边必关联两个结点,而一条边给予关联的每个结点的 度数为 1。因此在每个图中,结点度数总和等于边数的两倍。 5、定理 7-1.2:在任何图中,度数为奇数的结点的个数必为偶数。 6、定理 7-1.3:在任何有向图中,所有结点的入度之和等于所有结点 的出度之和。 证明 因为每一条有向边必对应一个入度和一个出度,若一个结点具有 一个入度或出度,则必关联一条有向边,所以有向图中,各结点入度 之和等于边数,各结点出度之和也等于边数 。因此,在任何有向图中, 所有结点的入度之和等于所有结点的出度之和。 三、特殊的图 1、多重图 定义 7-1.4:含有平行边的图称为多重图。 2、简单图:不含平行边和环的图称为简单图。 3、完全图 定义 7-1.5:简单图 G=<V,E>中,若每一对结点间均有边相连,则称 该图为完全图。 v1 v2 v1 v3 v4 v2 G1 G2