
一、填空20%(每小题2分) 1.设A={x(x∈N)且(x<5)以,B={xx∈E且x<7乃(N:自然数集,E正偶数)则 AUB= 2.A,B,C表示三个集合,文图中阴影部分的集合表达式为 A B 3.设P,Q的真值为0,R,S的真值为1,则 一(Pv(Q→(RAP)→(RV一S)的真值 4.公式(PAR)V(SAR)V一P的主合取范式为 5.若解释I的论域D仅包含一个元素,则3xPx)→xPx)在I下真值为 6.设A={1,2,3,4},A上关系图为 则R2= 7.设A={a,b,c,d,其上偏序关系R的哈斯图为 则R=
88c5e86133244bddae6346dbffb1a6cc.doc 1 一、填空 20% (每小题 2 分) 1.设 = { | ( ) ( 5)}, = { | 7} + A x x N 且 x B x x E 且x (N:自然数集,E + 正偶数) 则 A B = 。 2.A,B,C 表示三个集合,文图中阴影部分的集合表达式为 。 3.设 P,Q 的真值为 0,R,S 的真值为 1,则 (P (Q → (R P))) → (R S) 的真值= 。 4.公式 (P R) (S R) P 的主合取范式为 。 5.若解释 I 的论域 D 仅包含一个元素,则 xP(x) → xP(x) 在 I 下真值为 。 6.设 A={1,2,3,4},A 上关系图为 则 R 2 = 。 7.设 A={a,b,c,d},其上偏序关系 R 的哈斯图为 则 R= 。 A B C
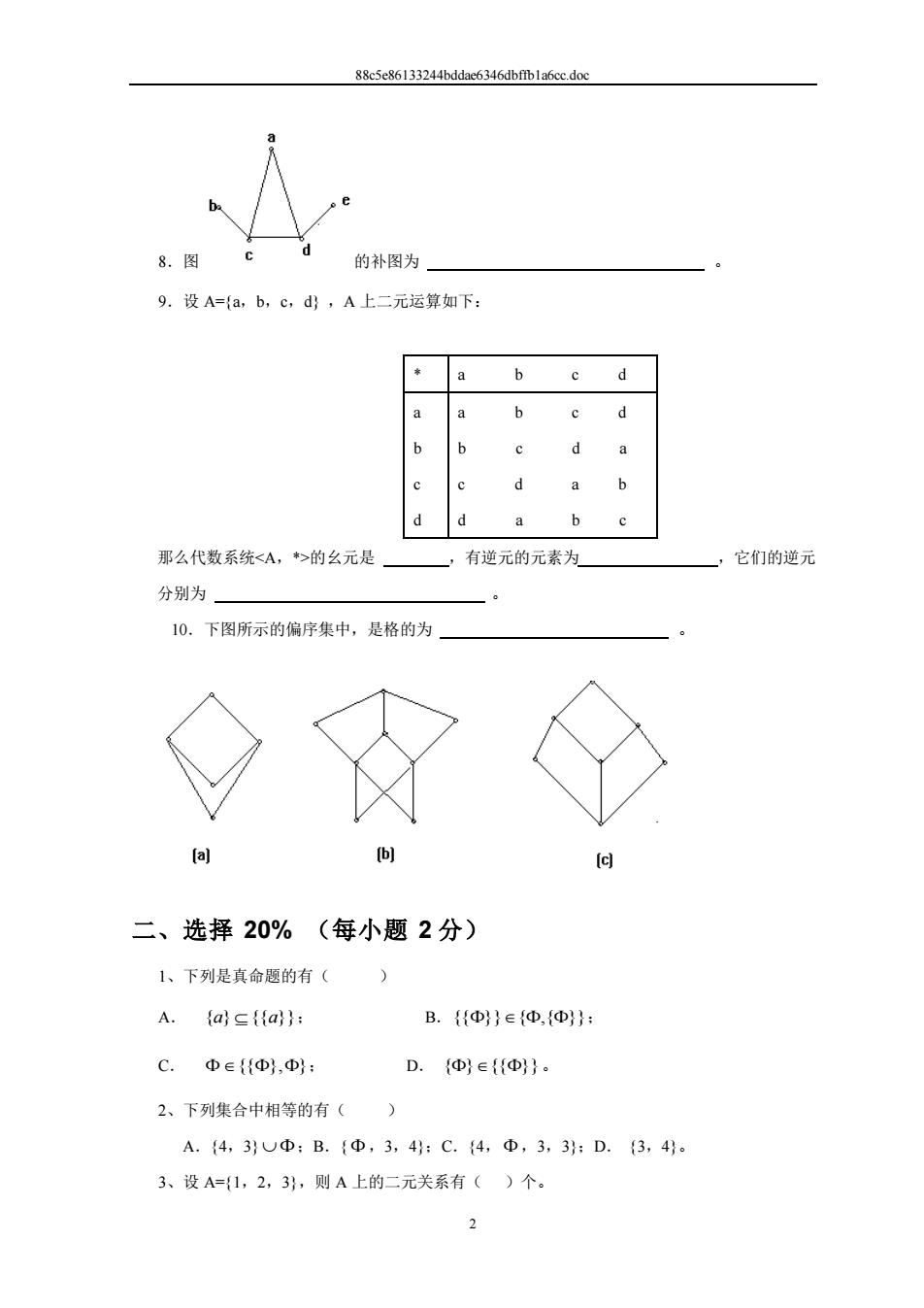
的补图为 9.设A={a,b,c,d},A上二元运算如下: a b c d bc d b 6 d a b a 那么代数系统<A,>的么元是 有逆元的元素为 它们的逆元 分别为 10.下图所示的偏序集中,是格的为 b 二、选择20%(每小题2分) 1、下列是真命题的有( A.a(a): B.{Φ}e中,Φ}: C.Φe{Φ},D}: D.{Φ}∈{}. 2、下列集合中相等的有() A.4,3}U④:B.{④,3,4:C.4,①,3,3:D.{3,4}。 3、设A=1,2,3},则A上的二元关系有()个
88c5e86133244bddae6346dbffb1a6cc.doc 2 8.图 的补图为 。 9.设 A={a,b,c,d} ,A 上二元运算如下: * a b c d a b c d a b c d b c d a c d a b d a b c 那么代数系统<A,*>的幺元是 ,有逆元的元素为 ,它们的逆元 分别为 。 10.下图所示的偏序集中,是格的为 。 二、选择 20% (每小题 2 分) 1、下列是真命题的有( ) A. {a} {{a}} ; B.{{}}{,{}} ; C. {{},} ; D. {}{{}}。 2、下列集合中相等的有( ) A.{4,3} ;B.{ ,3,4};C.{4, ,3,3};D. {3,4}。 3、设 A={1,2,3},则 A 上的二元关系有( )个
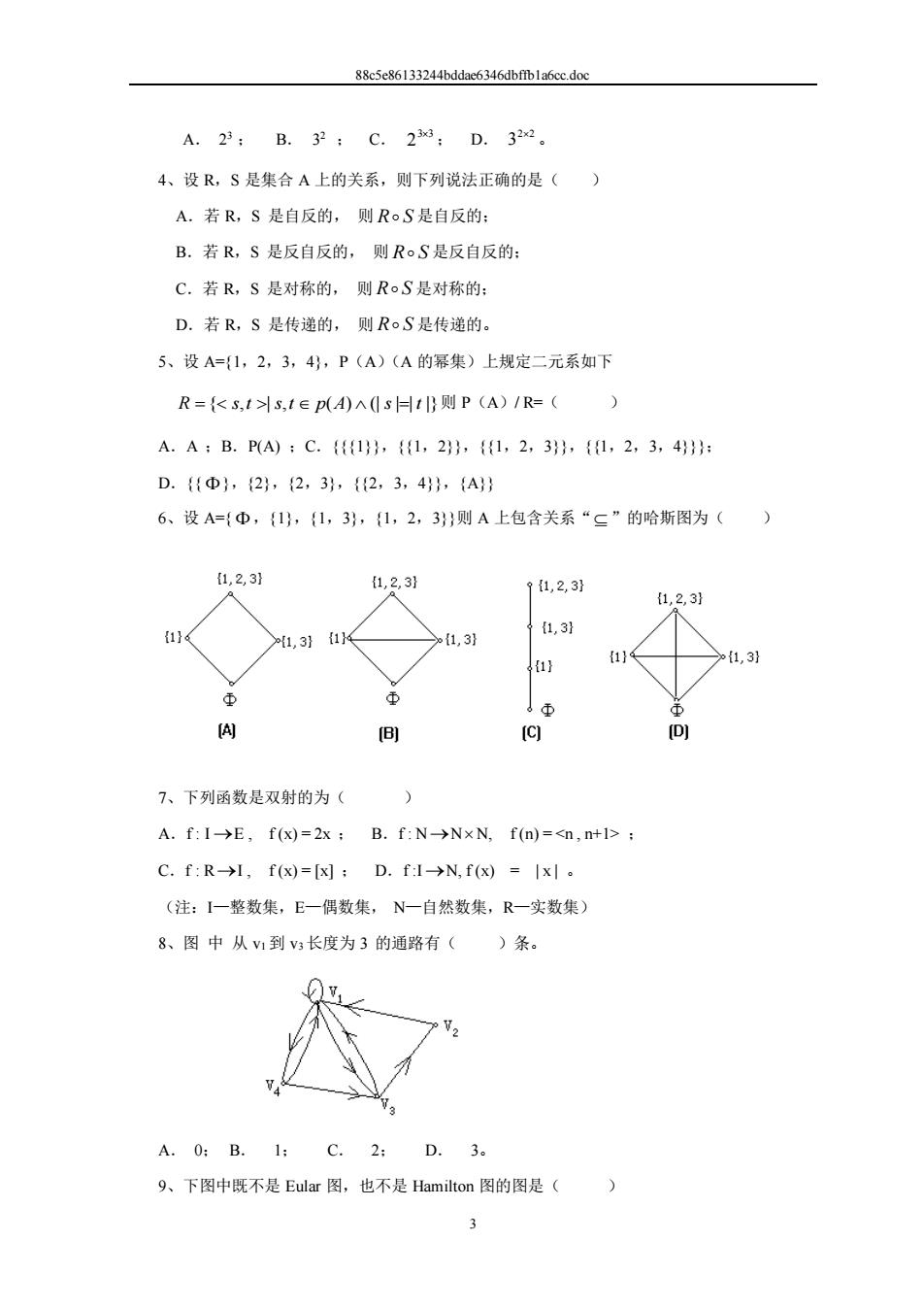
A.23B.32C.2:D.322. 4、设R,S是集合A上的关系,则下列说法正确的是() A.若R,S是自反的,则RoS是自反的: B.若R,S是反自反的,则R。S是反自反的 C.若R,S是对称的,则RoS是对称的: D.若R,S是传递的,则RoS是传递的。 5、设A=(1,2,3,4,P(A)(A的幂集)上规定二元系如下 R={K3,1>3,1∈p(A)A(s曰1}则P(A)1R=() A.A:B.PA:C.{1,{1,2,{1,2,3,{1,2,3,4: D.D,{2,2,3,{2,3,4,{A} 6、设A={中,1,3,{1,2,3则A上包含关系“”的哈斯图为( 1,2,3引 11,2,3引 0 7、下列函数是双射的为( A.f:I>E,fx)=2x:B.f:N→N×N,f(n)=<n,t1> C.f:R→,fx)=x:D.f→N,fx)=Ix。 (注:【一整数集,E一偶数集,N一自然数集,R一实数集) 8、图中从1到v长度为3的通路有()条。 A.0B.1: C.2: D.3。 9、下图中既不是Eular图,也不是Hamilton图的图是( 3
88c5e86133244bddae6346dbffb1a6cc.doc 3 A. 2 3 ; B. 3 2 ; C. 3 3 2 ; D. 2 2 3 。 4、设 R,S 是集合 A 上的关系,则下列说法正确的是( ) A.若 R,S 是自反的, 则 R S 是自反的; B.若 R,S 是反自反的, 则 R S 是反自反的; C.若 R,S 是对称的, 则 R S 是对称的; D.若 R,S 是传递的, 则 R S 是传递的。 5、设 A={1,2,3,4},P(A)(A 的幂集)上规定二元系如下 R = { s,t | s,t p(A) (| s |=| t |} 则 P(A)/ R=( ) A.A ;B.P(A) ;C.{{{1}},{{1,2}},{{1,2,3}},{{1,2,3,4}}}; D.{{ },{2},{2,3},{{2,3,4}},{A}} 6、设 A={ ,{1},{1,3},{1,2,3}}则 A 上包含关系“ ”的哈斯图为( ) 7、下列函数是双射的为( ) A.f : I → E , f (x) = 2x ; B.f : N → N N, f (n) = <n , n+1> ; C.f : R → I , f (x) = [x] ; D.f :I → N, f (x) = | x | 。 (注:I—整数集,E—偶数集, N—自然数集,R—实数集) 8、图 中 从 v1 到 v3 长度为 3 的通路有( )条。 A. 0; B. 1; C. 2; D. 3。 9、下图中既不是 Eular 图,也不是 Hamilton 图的图是( )

△⊕X☒ B 10、在一棵树中有7片树叶,3个3度结点,其余都是4度结点则该树有()个4度结 点。 A.1:B.2:C.3:D.4。 三、证明26% 1、R是集合X上的一个自反关系,求证:R是对称和传递的,当且仅当 <a,b>和<a,心在R中有<b,c心在R中。(8分) 2、f和g都是群<G,★>到kG2,>的同态映射,证明<C,★>是<G,★>的一个子群。 其中C={xx∈G,且f(x)=g(x)}(8分) 3、G=<VE>(M=v,旧=-e)是每一个面至少由k(k之3)条边围成的连通平面图, 四、逻辑推演16% 用CP规则证明下题(每小题8分) 1、AVB→CAD,DyE→F→A→F 2、x(P(x)→Qx》=xPx)→xQx) 五、计算18% 1、设集合A={a,b,c,d上的关系R={a,b>,<b,a>,<b,c>,<c,d>}用矩阵运算求出R 的传递闭包t(R)。 (9分)
88c5e86133244bddae6346dbffb1a6cc.doc 4 10、在一棵树中有 7 片树叶,3 个 3 度结点,其余都是 4 度结点则该树有( )个 4 度结 点。 A.1;B.2; C.3; D.4 。 三、证明 26% 1、R 是集合 X 上的一个自反关系,求证:R 是对称和传递的,当且仅当 < a, b> 和<a , c>在 R 中有<.b , c>在 R 中。(8 分) 2、f 和 g 都是群<G1 ,★>到< G2, *>的同态映射,证明<C , ★>是<G1, ★>的一个子群。 其中 C= { | ( ) ( )} 1 x xG 且f x = g x (8 分) 3、G=<V, E> (|V| = v,|E|=e ) 是每一个面至少由 k(k 3)条边围成的连通平面图, 则 2 ( 2) − − k k v e , 由此证明彼得森图(Peterson)图是非平面图。(11 分) 四、逻辑推演 16% 用 CP 规则证明下题(每小题 8 分) 1、 A B → C D, D E → F A → F 2、x(P(x) → Q(x)) x P(x) → x Q(x) 五、计算 18% 1、设集合 A={a,b,c,d}上的关系 R={<a , b > ,< b , a > ,< b, c > , < c , d >}用矩阵运算求出 R 的传递闭包 t (R)。 (9 分)

2、如下图所示的赋权图表示某七个城市y,y2,.,及预先算出它们之间的一些直接通信线 路造价,试给出一个设计方案,使得各城市之间能够通信而且总造价最小。(9分) 1收202 29/ 49
88c5e86133244bddae6346dbffb1a6cc.doc 5 2、如下图所示的赋权图表示某七个城市 1 2 7 v ,v , ,v 及预先算出它们之间的一些直接通信线 路造价,试给出一个设计方案,使得各城市之间能够通信而且总造价最小。 (9分)