
离散数学试卷(九) 一、 填空30%(每空3分) 1、选择合适的论域和谓词表达集合A=“直角坐标系中,单位元(不包括单位圆周)的点集 则A=」 。 2、集合A={D,{}的幂集PA)= 3、设A={1,2,3,4,A上二元关系R=<1,2>,<2,1>,<2,3>,<3,4画出R的关 系图 4、设A={<1,2>,<2,4>,3,3>},B=1,3>,2,4,<4,21, 则AUB= AoB= 5、设A3,则A上有 个二元关系 6、A={1,2,3上关系R 时,R既是对称的又是反对称的, 7、偏序集<AR>的哈斯图为 则R= 8、设X=m,Y=m则(1)从X到Y有 个不同的函数。 (2)当n,m满足 一时,存在双射有 二个不同的双射。 9、√2是有理数的真值为 10、Q:我将去上海,R:我有时间,公式(Q→R)A(R→Q)的 自然语言为 11、公式(Q→P)A(-PAQ)的 主合取范式是 若S={S,S2,S}是集合A的一个分划
离散数学试卷(九) 55 一、 填空 30% (每空 3 分) 1、 选择合适的论域和谓词表达集合 A=“直角坐标系中,单位元(不包括单位圆周)的点集” 则 A= 。 2、 集合 A={ ,{ }}的幂集 P(A) = 。 3、 设 A={1,2,3,4},A 上二元关系 R={<1,2>,<2,1>,<2,3>,<3,4>}画出 R 的关 系图 。 4、 设 A={<1,2>,<2 , 4 >,<3 , 3 >} , B={<1,3>,<2,4>,<4,2>}, 则 A B = 。 A B = 。 5、 设|A|=3,则 A 上有 个二元关系。 6、 A={1,2,3}上关系 R= 时,R 既是对称的又是反对称的。 7、 偏序集 A,R 的哈斯图为 , 则 R = 。 8、 设|X|=n,|Y|=m 则(1)从 X 到 Y 有 个不同的函数。 (2)当 n , m 满足 时,存在双射有 个不同的双射。 9、 2 是有理数的真值为 。 10、 Q:我将去上海,R:我有时间,公式 (Q → R) (R → Q) 的 自然语言为 。 11、 公式 (Q → P) (P Q) 的 主合取范式是 。 12、 若 { , , , } S = S1 S2 Sm 是集合 A 的一个分划

离散数学试卷(九) 则它应满足 二、选择20%(每小题2分) 1、设全集为1,下列相等的集合是( )。 A、A={xx是偶数或奇数:B、B={x3y∈1Ax=2y)》: C、C={x|30ye1Ax=2y+1)}:D、D={x|0,1-1,2,-2,3,-3,4,-4,}。 2、设S={N,Q,R,下列命题正确的是( )。 A、2∈N,N∈S则2∈S:B、NcQ,Q∈S则NcS: C、NcQ,QcR则NcR:D、ΦcN,ΦcS则中cNOS。 3设CaBa则与Q5分别为( A、C和{ab:B、{ab;与④:C、{ab}与ab:D、C与C 4、下列语句不是命题的有( )。 A、x=13:B、离散数学是计算机系的一门必修课:C、鸡有三只脚: D、太阳系以外的星球上有生物:E、你打算考硕士研究生吗? 5、(P→Q)→R的合取范式为( )。 A、(PA一Q)VR:B、(PVR)A(-QVR): C、 (PA-0AR)V(PA-0A-R)V(PAOAR)V(PA-OAR)V(-PAOAR)V(-PA-0AR) D、(PVOVR)A(PV-OVR)A(PV-OVR)A(-PV-QVR)。 6、设Am,则A上有()二元关系。 A、2:B、m2:C2;D、mE、2。 7、设r为集合A上的相容关系,其简化关系图(如图), 则四r产生的最大相容类为(): A、{x,x2}:B、{1,x2,x}:C、{x4,x:D、{2,x4,x} 第7题 四A的完全覆盖为( )
离散数学试卷(九) 56 则它应满足 。 二、 选择 20% (每小题 2 分) 1、 设全集为 I,下列相等的集合是( )。 A、 A ={x | x是偶数或奇数} ; B、 B = {x | y( y I x = 2y)} ; C、C = {x | y( y I x = 2y +1)} ; D、 D = {x | 0,1,−1,2,−2,3,−3,4,−4, }。 2、 设 S={N,Q,R},下列命题正确的是( )。 A、 2 N,N S 则2S ; B、 N Q,QS 则 N S ; C、 N Q,Q R 则 N R ; D、 N, S 则 N S 。 3、 设 C={{a},{b},{a,b}},则 S S S C S C 与 分别为( )。 A、C 和{a,b};B、{a,b}与 ;C、{a,b}与{a,b};D、C 与 C 4、 下列语句不是命题的有( )。 A、 x=13; B、离散数学是计算机系的一门必修课; C、鸡有三只脚; D、太阳系以外的星球上有生物; E、你打算考硕士研究生吗? 5、 (P → Q) → R 的合取范式为( )。 A、 (P Q) R ;B、(P R) (Q R) ; C、 (P Q R) (P Q R) (P Q R) (P Q R) (P Q R) (P Q R) D、 (P Q R) (P Q R) (P Q R) (P Q R) 。 6、 设|A|=n,则 A 上有()二元关系。 A、2 n ; B、n 2 ; C、 2 2 n ; D、n n ; E、 n n 2 。 7、 设 r 为集合 A 上的相容关系,其简化关系图(如图), 则 [I] r 产生的最大相容类为( ); A、{ , } 1 2 x x ; B、{ , , } 1 2 3 x x x ; C、{ , } 4 5 x x ; D、{ , , } 2 4 5 x x x [II] A 的完全覆盖为( )
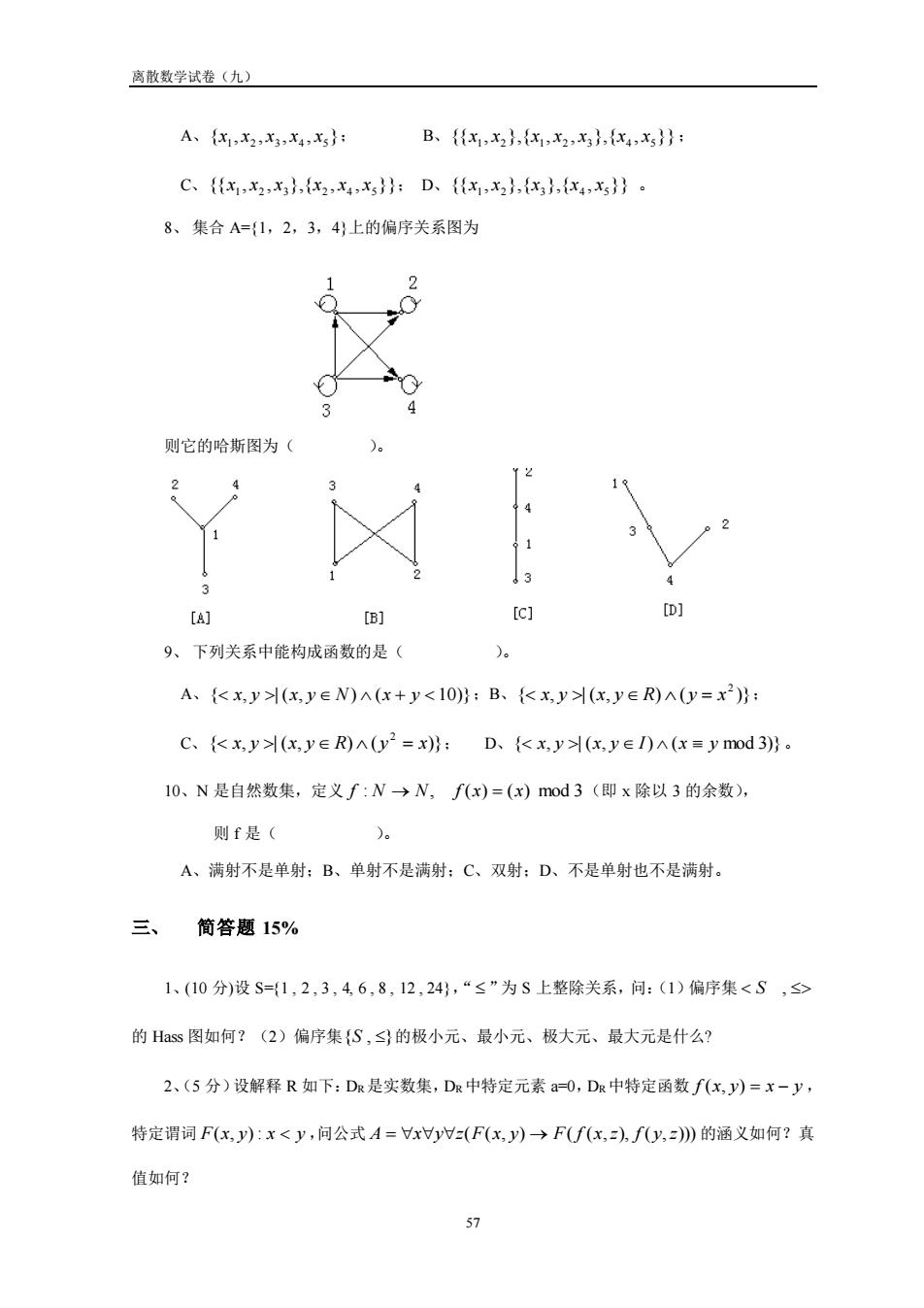
离散数学试卷(九) A、{x1,x2,x3,x4,x3} B、{x1,x2,{x1,x2,x3,{x4,x3} C、{x1,x2,x3},{2,4,}:D、{x1,x2},{3},{x4,5}。 8、集合A=1,2,3,4上的偏序关系图为 则它的哈斯图为( )。 3 [A] [B] [D] 9、下列关系中能构成函数的是( A、{Kxy(xy∈N)A(x+y<I0)}:B、{Kxy(,y∈R)A(y=x2)} C、{Kx,y(x,y∈R)A0y2=x)}:D、{kx,y(x,ye)A(x=ymod3}. 10、N是自然数集,定义f:N→N,f(x)=(x)mod3(即x除以3的余数), 则f是( )。 A、满射不是单射:B、单射不是满射:C、双射:D、不是单射也不是满射。 三、简答题15% 1、(10分)设S=(1,2,3,46,8,12,24),“≤”为S上整除关系,问:(1)偏序集<S,s> 的Hs图如何?(2)偏序集{S,≤的极小元、最小元、极大元、最大元是什么? 2、(5分)设解释R如下:Dr是实数集,Dg中特定元素a=0,Da中特定函数f(x,y)=x-y, 特定谓词F(x,y):x<y,问公式A=xy=(F(x,y)→Ff(x,),fy,)的涵义如何?真 值如何?
离散数学试卷(九) 57 A、{ , , , , } 1 2 3 4 5 x x x x x ; B、{{ , },{ , , },{ , }} 1 2 1 2 3 4 5 x x x x x x x ; C、{{ , , },{ , , }} 1 2 3 2 4 5 x x x x x x ; D、{{ , },{ },{ , }} 1 2 3 4 5 x x x x x 。 8、 集合 A={1,2,3,4}上的偏序关系图为 则它的哈斯图为( )。 9、 下列关系中能构成函数的是( )。 A、{ x, y | (x, y N) (x + y 10)} ;B、{ , | ( , ) ( )} 2 x y x y R y = x ; C、{ , | ( , ) ( )} 2 x y x y R y = x ; D、{ x, y | (x, y I) (x y mod 3)}。 10、N 是自然数集,定义 f : N → N, f (x) = (x) mod 3 (即 x 除以 3 的余数), 则 f 是( )。 A、满射不是单射;B、单射不是满射;C、双射;D、不是单射也不是满射。 三、 简答题 15% 1、(10 分)设 S={1 , 2 , 3 , 4, 6 , 8 , 12 , 24},“ ”为 S 上整除关系,问:(1)偏序集 S , 的 Hass 图如何?(2)偏序集 {S , } 的极小元、最小元、极大元、最大元是什么? 2、(5 分)设解释 R 如下:DR是实数集,DR中特定元素 a=0,DR中特定函数 f (x, y) = x − y , 特定谓词 F(x, y) : x y ,问公式 A = xyz(F(x, y) → F( f (x,z), f ( y,z))) 的涵义如何?真 值如何?

离散数学试卷(九) 四、逻辑推理10% 或者逻辑难学,或者有少数学生不喜欢它:如果数学容易学,那么逻辑并不难学。因此,如 果许多学生喜欢逻,那么数学并不难学。 五、10% 设X=12,3,45,X上的关系R=<1,1>,<1,2>,2,4>,<3,5>,<4,2>},用Warshall 方法,求R的传递闭包t(R)。 六、证明15% 1、每一有限全序集必是良序集。(7分) 2、设g0∫是复合函数,如果g0∫满射,则g也是满射。(8分)
离散数学试卷(九) 58 四、 逻辑推理 10% 或者逻辑难学,或者有少数学生不喜欢它;如果数学容易学,那么逻辑并不难学。因此,如 果许多学生喜欢逻辑,那么数学并不难学。 五、10% 设 X={1,2,3,4,5},X 上的关系 R={<1,1> , < 1 , 2 > , <2 , 4 > , < 3 , 5 > , < 4 , 2 > },用 Warshall 方法,求 R 的传递闭包 t (R)。 六、证明 15% 1、 每一有限全序集必是良序集。(7 分) 2、 设 g f 是复合函数,如果 g f 满射,则 g 也是满射。(8 分)