
离散数学试卷(二) 一、填空20%(每小题2分) 1、P:你努力,Q:你失败。“除非你努力,否则你将失败”的翻译为 :“虽然你努力了,但还是失败了”的翻译为 2、论域D=1,2,指定谓词P P(1.1) P(1,2)P(2,1)P(2,2) T 则公式x3P(y,x)真值为 2、设S={a,s,B是S的子集,则由Bs1所表达的子集是 3、设A={2,3,4,5,6)上的二元关系R={kx,yx<yVx是质数,则R= 。(列举法)。 R的关系矩阵M 5、设A=1,2,3头,则A上既不是对称的又不是反对称的关系R= A上既是对称的又是反对称的关系R= 6、设代数系统<A,>,其中A={a,b,c, a b 则幺元是 .:是否有幂等c 性一:是否有对称性 7、4阶群必是 ,群或 群 8、下面偏序格是分配格的是 第1页共4页
离散数学试卷(二) 第 1 页 共 4 页 一、填空 20% (每小题 2 分) 1、 P:你努力,Q:你失败。“除非你努力,否则你将失败”的翻译为 ;“虽然你努力了,但还是失败了”的翻译为 。 2、论域 D={1,2},指定谓词 P P (1,1) P (1,2) P (2,1) P (2,2) T T F F 则公式 xyP( y, x) 真值为 。 2、 设 S={a1 ,a2 ,.,a8},Bi 是 S 的子集,则由 B31 所表达的子集是 。 3、 设 A={2 , 3 , 4 , 5 , 6} 上 的 二 元 关 系 R ={ x, y | x y x是质数} , 则 R= (列举法)。 R 的关系矩阵 MR= 。 5、设 A={1,2,3},则 A 上既不是对称的又不是反对称的关系 R= ; A 上既是对称的又是反对称的关系 R= 。 6、设代数系统<A,*>,其中 A={a,b,c}, 则幺元 是 ;是否有幂等 性 ;是否有对称性 。 7、4 阶群必是 群或 群。 8、下面偏序格是分配格的是 。 * a b c a b c a b c b b c c c b

离散数学试卷(二) (A) (B) (c 9、n个结点的无向完全图K的边数为 欧拉图的充要条件是 10、公式(PV(一PAQ》A(-PvQ)A一R的根树表示为 二、选择20%(每小题2分) 1、在下述公式中是重言式为( A.(PAQ)→(PVQ):B.(PQ)(P→Q)A(Q→P): C.(P→Q)AQ:D.P→(PvQ)。 2、命题公式(一P→Q)→(一QVP)中极小项的个数为( ),成真赋值的个数为 () A.0:B.1:C.2:D.3。 3、设S={中,{,1,2},则25有()个元素 A.3:B.6:C.7:D.8 4、设S={1,2,3},定义S×S上的等价关系 R={k<a,b>,<c,d>l<a,b>eSxS,<c,d>eS×S,a+d=b+c则由R产生的 SxS上一个划分共有( )个分块。 A.4:B.5:C.6:D.9. 5、设S-{1,2,3},S上关系R的关系图为 第2页共4页
离散数学试卷(二) 第 2 页 共 4 页 9、n 个结点的无向完全图 Kn 的边数为 ,欧拉图的充要条件是 。 10、公式 (P (P Q)) ((P Q) R 的根树表示为 。 二、选择 20% (每小题 2 分) 1、在下述公式中是重言式为( ) A. (P Q) → (P Q) ;B.(P Q) ((P → Q) (Q → P)) ; C. (P → Q) Q ; D. P → (P Q) 。 2、命题公式 (P → Q) → (Q P) 中极小项的个数为( ),成真赋值的个数为 ( )。 A.0; B.1; C.2; D.3 。 3、设 S = {,{1},{1,2}} ,则 S 2 有( )个元素。 A.3; B.6; C.7; D.8 。 4、 设 S = {1, 2, 3} ,定义 S S 上的等价关系 R = { a,b , c,d | a,b S S, c,d S S,a + d = b + c} 则由 R 产 生的 S S 上一个划分共有( )个分块。 A.4; B.5; C.6; D.9 。 5、设 S = {1, 2, 3},S 上关系 R 的关系图为
离散数学试卷(二) ① ② 则R具有( )性质。 A,自反性、对称性、传递性: B.反自反性、反对称性: C.反自反性、反对称性、传递性: D.自反性。 6、设+,。为普通加法和乘法,则( )<S,+,0>是域。 A.S=xlx=a+b3,a,beQ)B.S=(xlx=2n,a,bEZ) C.S=xx=2n+1,nEZ} D.S={x|x∈ZAx20}=N。 7、下面偏序集()能构成格。 X分 B IC) 8、在如下的有向图中,从V1到V:长度为3的道路有( A.1:B.2:C.3: D.4 9、在如下各图中()欧拉图。 A (1 是实数集合,“×”为普通乘法,则代数系统<R,是( 第3页共4页
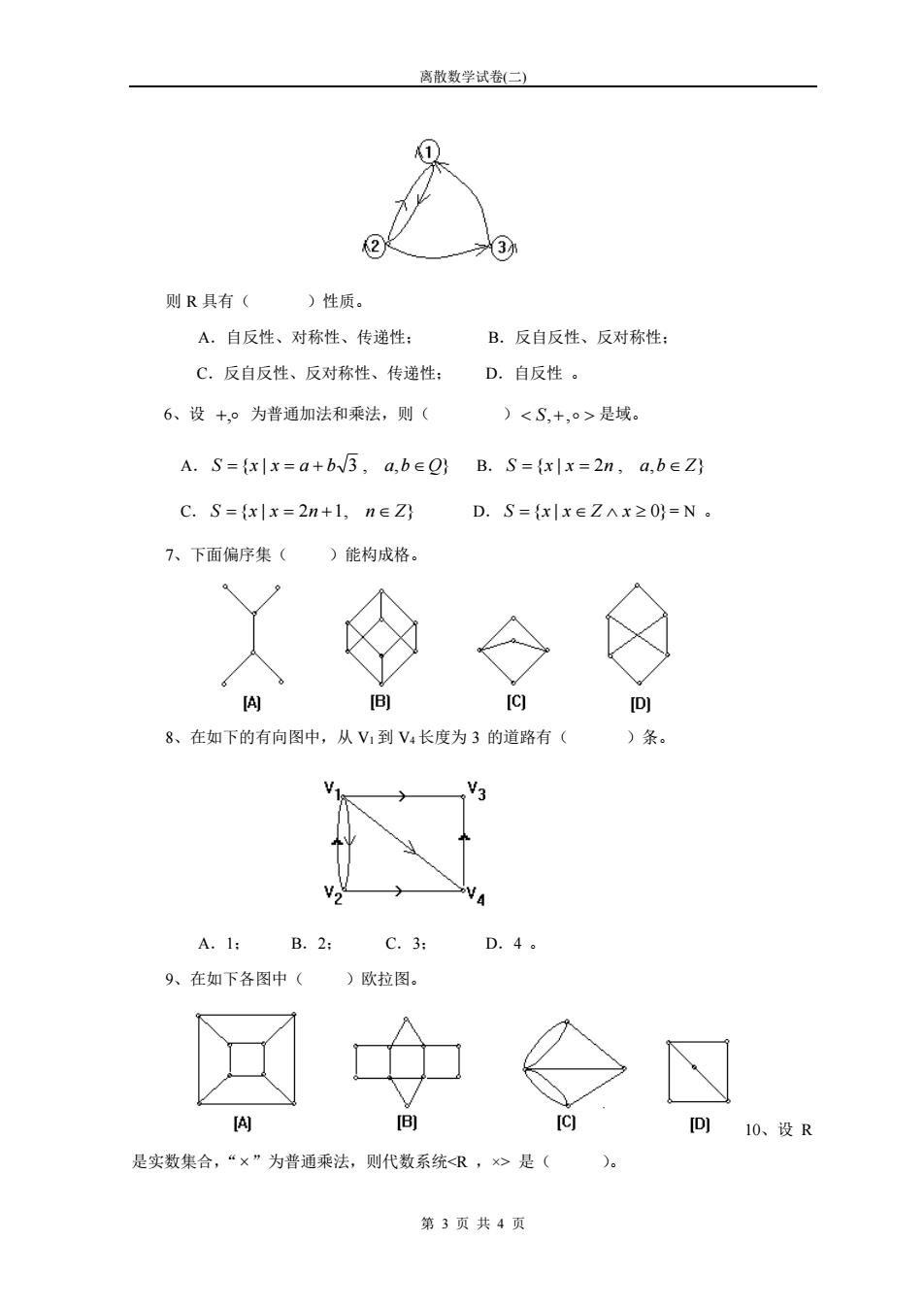
离散数学试卷(二) 第 3 页 共 4 页 则 R 具有( )性质。 A.自反性、对称性、传递性; B.反自反性、反对称性; C.反自反性、反对称性、传递性; D.自反性 。 6、设 +, 为普通加法和乘法,则( ) S,+, 是域。 A. S = {x | x = a + b 3 , a,b Q} B. S = {x | x = 2n , a,b Z} C. S = {x | x = 2n +1, n Z} D. S = {x | x Z x 0} = N 。 7、下面偏序集( )能构成格。 8、在如下的有向图中,从 V1 到 V4 长度为 3 的道路有( )条。 A.1; B.2; C.3; D.4 。 9、在如下各图中( )欧拉图。 10、设 R 是实数集合,“ ”为普通乘法,则代数系统<R ,×> 是( )

离散数学试卷(二) A.群: B.独异点:C.半群。 三、证明46% 1、设R是A上一个二元关系, S={Ka,b(a,b∈A)A(对于某一个c∈A有<a,c>eR且<c,b>eR}试证明若R 是A上一个等价关系,则S也是A上的一个等价关系。(9分) 2、用逻辑推理证明: 所有的舞蹈者都很有风度,王华是个学生且是个舞蹈者。因此有些学生很有风度。(1 分) 3、若:A→B是从A到B的函数,定义一个函数g:B→2对任意b∈B有 g(b)={xI(x∈A)A(f(x)=b)},证明:若f是A到B的满射,则g是从B到24的 单射。(10分) 4、若无向图G中只有两个奇数度结点,则这两个结点一定连通。(8分) 5、设G是具有n个结点的无向简单图,其边数m=n-lXn-2)+2,则G是miom 图(8分) 四、计算14% 1、设<76,+>是一个群,这里+s是模6加法,76=0],[,[☑,3队,4,[,试求 出<Z6,+6>的所有子群及其相应左陪集。(7分) 2、权数1,4,9,16,25,36,49,64,81,100构造一棵最优二叉树。(7分) 第4页共4页
离散数学试卷(二) 第 4 页 共 4 页 A.群; B.独异点; C.半群 。 三、证明 46% 1、 设 R 是 A 上一个二元关系, S ={ a,b | (a,b A) (对于某一个c A, 有 a,c R且 c,b R)} 试证明若 R 是 A 上一个等价关系,则 S 也是 A 上的一个等价关系。(9 分) 2、 用逻辑推理证明: 所有的舞蹈者都很有风度,王华是个学生且是个舞蹈者。因此有些学生很有风度。(11 分) 3、 若 f : A → B 是从 A 到 B 的函数,定义一个函数 A g : B → 2 对任意 bB 有 g(b) = {x | (x A) ( f (x) = b)} ,证明:若 f 是 A 到 B 的满射,则 g 是从 B 到 A 2 的 单射。(10 分) 4、 若无向图 G 中只有两个奇数度结点,则这两个结点一定连通。(8 分) 5、 设 G 是具有 n 个结点的无向简单图,其边数 ( 1)( 2) 2 2 1 m = n − n − + ,则 G 是 Hamilton 图(8 分) 四、计算 14% 1、 设<Z6,+6>是一个群,这里+6 是模 6 加法,Z6={[0 ],[1],[2],[3],[4],[5]},试求 出<Z6,+6>的所有子群及其相应左陪集。(7 分) 2、 权数 1,4,9,16,25,36,49,64,81,100 构造一棵最优二叉树。(7 分)