
离散数学教案 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组
离散数学教案 1 《离散数学》课程教学教案 内蒙古农业大学计算机与信息工程学院 《离散数学》课程建设组

离散数学教案 《离散数学(一)》教学教案 第一部分课程总论 一、课程简介 课程名称:离散数学 英文名称:Discrete Mathematics 离散数学:离散数学是现代数学的一个重要分支,是计算机科学的核心课程。以 研究离散量的结构和相互间的关系为主要目标,其研究对象是有限个或无限个元素。 离散数学与计算机科学中的数据结构、操作系统、编译理论、算法分析、逻辑设计、 系统结构、容错诊断、机器定理证明等课程紧密相关。是一门重要的基础课程。 数学内容:数理逻辑、集合论、代数系统和图论和共四部分。 数学要求:通过该课程的学习,培养和锻炼抽象思维和缜密概括的能力,为专业 基础课和专业课的学习打下坚实的理论基础。 授课总学时:4学时/周×16周=64学时 二、适用对象 本课程教学教案主要针对计算机科学与技术和网络工程本科专业 三、学习要领 概念(正确):必须掌握好离散数学中大量的概念 判断(准确):根据概念对事物的属性进行判断 推理(可靠):根据多个判断推出一个新的判断 四、离散数学与计算机的关系 第一部分数理逻辑 计算机是数理逻辑和电子学相结合的产物 第二部分集合论 集合:一种重要的数据结构 关系:关系数据库的理论基础 函数:所有计算机语言中不可缺少的一部分 第三部分代数系统 计算机编码和纠错码理论 数字逻辑设计基础 计算机使用的各种运算 第四部分图论 2
离散数学教案 2 《离散数学(一)》教学教案 第一部分 课程总论 一、课程简介 课程名称:离散数学 英文名称:Discrete Mathematics 离散数学:离散数学是现代数学的一个重要分支,是计算机科学的核心课程。以 研究离散量的结构和相互间的关系为主要目标,其研究对象是有限个或无限个元素。 离散数学与计算机科学中的数据结构、操作系统、编译理论、算法分析、逻辑设计、 系统结构、容错诊断、机器定理证明等课程紧密相关。是一门重要的基础课程。 教学内容:数理逻辑、集合论、代数系统和图论和共四部分。 教学要求:通过该课程的学习,培养和锻炼抽象思维和缜密概括的能力,为专业 基础课和专业课的学习打下坚实的理论基础。 授课总学时: 4 学时/周 16 周 = 64 学时 二、适用对象 本课程教学教案主要针对计算机科学与技术和网络工程本科专业 三、学习要领 概念(正确):必须掌握好离散数学中大量的概念 判断(准确):根据概念对事物的属性进行判断 推理(可靠):根据多个判断推出一个新的判断 四、离散数学与计算机的关系 第一部分 数理逻辑 计算机是数理逻辑和电子学相结合的产物 第二部分 集合论 集合:一种重要的数据结构 关系:关系数据库的理论基础 函数:所有计算机语言中不可缺少的一部分 第三部分 代数系统 计算机编码和纠错码理论 数字逻辑设计基础 计算机使用的各种运算 第四部分 图论

离散数学教案 数据结构、操作系统、编译原理、计算机网络原理的基础 五、教材及主要参考书 教材: 左孝凌、李为鑑、刘永才,离散数学,上海科学技术出版社,1982年9月第1 版。 参考书: [1)王元元、张桂芸,离散数学导论,科学出版社,2002 [2]Kenneth H.Rosen Discrete Mathematics and Its Applications Fourth Edition),机械工业出版社(华章),2001 [3)】王元元、张桂芸,计算机科学中的离散结构,机械工业出版社,2004 [4]Bernard Kolman,Robert C.Busby,Sharon Ross,Discrete Mathematical Structures(Fourth Edition),高等教育出版社,2O01 [⑤)孙吉贵杨凤杰欧阳丹彤李占山,离散数学,高等教育出版社,2002 [6马振华,离散数学导引,清华大学出版社,1993 [7)王树禾,离散数学引论,中国科技大学出版社,2001 [8]Andrew Simpon著冯速译离散数学导学机械工业出版社2005
离散数学教案 3 数据结构、操作系统、编译原理、计算机网络原理的基础 五、教材及主要参考书 教材: 左孝凌、李为鑑、刘永才,离散数学,上海科学技术出版社,1982 年 9 月第 1 版。 参考书: [1] 王元元、张桂芸,离散数学导论,科学出版社,2002 [2] Kenneth H.Rosen Discrete Mathematics and Its Applications ( Fourth Edition), 机械工业出版社(华章),2001 [3] 王元元、张桂芸,计算机科学中的离散结构,机械工业出版社,2004 [4] Bernard Kolman , Robert C. Busby, Sharon Ross, Discrete Mathematical Structures (Fourth Edition), 高等教育出版社,2001 [5] 孙吉贵 杨凤杰 欧阳丹彤 李占山,离散数学, 高等教育出版社,2002 [6] 马振华,离散数学导引 ,清华大学出版社,1993 [7] 王树禾,离散数学引论,中国科技大学出版社,2001 [8] Andrew Simpon 著 冯速译 离散数学导学 机械工业出版社 2005
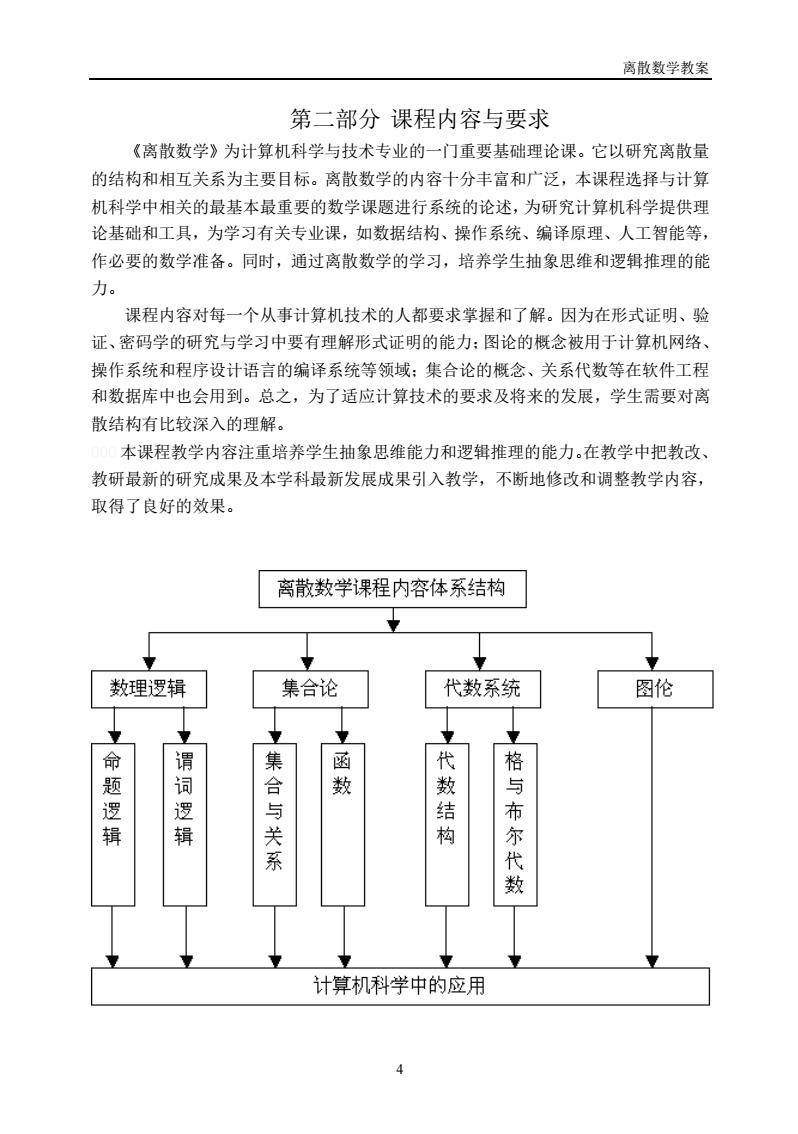
离散数学教案 第二部分课程内容与要求 《离散数学》为计算机科学与技术专业的一门重要基础理论课。它以研究离散量 的结构和相互关系为主要目标。离散数学的内容十分丰富和广泛,本课程选择与计算 机科学中相关的最基本最重要的数学课题进行系统的论述,为研究计算机科学提供理 论基础和工具,为学习有关专业课,如数据结构、操作系统、编译原理、人工智能等, 作必要的数学准备。同时,通过离散数学的学习,培养学生抽象思维和逻辑推理的能 力。 课程内容对每一个从事计算机技术的人都要求掌握和了解。因为在形式证明、验 证、密码学的研究与学习中要有理解形式证明的能力:图论的概念被用于计算机网络 操作系统和程序设计语言的编译系统等领域:集合论的概念、关系代数等在软件工程 和数据库中也会用到。总之,为了适应计算技术的要求及将来的发展,学生需要对离 散结构有比较深入的理解。 本课程教学内容注重培养学生抽象思维能力和逻辑推理的能力。在教学中把教改、 教研最新的研究成果及本学科最新发展成果引入教学,不断地修改和调整教学内容, 取得了良好的效果。 离散数学课程内容体系结构 数理逻辑 集合论 代数系统 图伦 命 谓 名 数 逻 逻 辑 辑 关 数结构 布尔 计算机科学中的应用
离散数学教案 4 第二部分 课程内容与要求 《离散数学》为计算机科学与技术专业的一门重要基础理论课。它以研究离散量 的结构和相互关系为主要目标。离散数学的内容十分丰富和广泛,本课程选择与计算 机科学中相关的最基本最重要的数学课题进行系统的论述,为研究计算机科学提供理 论基础和工具,为学习有关专业课,如数据结构、操作系统、编译原理、人工智能等, 作必要的数学准备。同时,通过离散数学的学习,培养学生抽象思维和逻辑推理的能 力。 课程内容对每一个从事计算机技术的人都要求掌握和了解。因为在形式证明、验 证、密码学的研究与学习中要有理解形式证明的能力;图论的概念被用于计算机网络、 操作系统和程序设计语言的编译系统等领域;集合论的概念、关系代数等在软件工程 和数据库中也会用到。总之,为了适应计算技术的要求及将来的发展,学生需要对离 散结构有比较深入的理解。 000 本课程教学内容注重培养学生抽象思维能力和逻辑推理的能力。在教学中把教改、 教研最新的研究成果及本学科最新发展成果引入教学,不断地修改和调整教学内容, 取得了良好的效果

离散数学教案 第一篇数理逻辑 逻辑学(1ogic) 是一门研究思维形式及思维规律的科学 数理逻辑(thematical logic) 是用数学的方法来研究人类推理过程的一门数学学科。 其显著特征是符号化和形式化,即把逻辑所涉及的“概念、判断、推理”用符号 来表示,用公理体系来刻划,并基于符号串形式的演算来描述推理过程的一般规律。 数理逻辑又称符号逻辑、现代逻辑。 命题逻辑 一、学习目的与要求 本章目的是介绍命题逻辑的基本概念。掌握利用命题逻辑表示自然语言,描述概 念、判断和推理。建立初步的语言形式化方法。 二、知识点 1.命题的概念、表示方法:联结词的逻辑意义。 2.命题公式的递归定义,自然语言翻译成命题公式 3.真值表的构造、命题公式等价的概念。 4.重言式与蕴涵式的定义、逻辑意义,逻辑等价与逻辑蕴涵的意义和证明方法。 常用的逻辑等价公式和逻辑蕴涵公式。 5.命题公式的对偶式、合取范式、析取范式、主合取范式、主析取范式。逻辑 小项、逻辑大项。任给公式化为析取范式、任给公式化为主析取范式、任给公式化为 合取范式、任给公式化为主合取范式。 6.命题逻辑的推理理论,主要的推理方法:真值表法、直接证明法、间接证明 法。常用推理规则:P规则、T规则、CP规则。 7.命题逻辑的应用示例。 三、要求 1.识记 命题表示方法、真值判断、命题公式的递归定义。 2.领会 联结词真值确定、翻译、命题公式的等价性和蕴涵性证明、任给公式化为析取范 式、任给公式化为主析取范式、任给公式化为合取范式、任给公式化为主合取范式。 3.简单应用 命题逻辑推理规则,命题逻辑设计简单的开关电路。 四、主要内容
离散数学教案 5 第一篇 数理逻辑 逻辑学( logic ) 是一门研究思维形式及思维规律的科学。 数理逻辑(mathematical logic) 是用数学的方法来研究人类推理过程的一门数学学科。 其显著特征是符号化和形式化,即把逻辑所涉及的“概念、判断、推理”用符号 来表示,用公理体系来刻划, 并基于符号串形式的演算来描述推理过程的一般规律。 数理逻辑又称符号逻辑、现代逻辑。 命题逻辑 一、学习目的与要求 本章目的是介绍命题逻辑的基本概念。掌握利用命题逻辑表示自然语言,描述概 念、判断和推理。建立初步的语言形式化方法。 二、知识点 1.命题的概念、表示方法;联结词的逻辑意义。 2.命题公式的递归定义,自然语言翻译成命题公式 3.真值表的构造、命题公式等价的概念。 4.重言式与蕴涵式的定义、逻辑意义,逻辑等价与逻辑蕴涵的意义和证明方法。 常用的逻辑等价公式和逻辑蕴涵公式。 5.命题公式的对偶式、合取范式、析取范式、主合取范式、主析取范式。逻辑 小项、逻辑大项。任给公式化为析取范式、任给公式化为主析取范式、任给公式化为 合取范式、任给公式化为主合取范式。 6.命题逻辑的推理理论,主要的推理方法:真值表法、直接证明法、间接证明 法。常用推理规则:P 规则、T 规则、CP 规则。 7.命题逻辑的应用示例。 三、要求 1.识记 命题表示方法、真值判断、命题公式的递归定义。 2.领会 联结词真值确定、翻译、命题公式的等价性和蕴涵性证明、任给公式化为析取范 式、任给公式化为主析取范式、任给公式化为合取范式、任给公式化为主合取范式。 3.简单应用 命题逻辑推理规则,命题逻辑设计简单的开关电路。 四、主要内容