
离散数学试卷(十一) 一、 填空20%(每小题2分) 1、 称为命题。 2、命题P一Q的真值为0,当且仅当」 3、一个命题含有4个原子命题,则对其所有可能赋值有 种。 4、所有小项的析取式为 5、令P(x):x是质数,E(x):X是偶数,Q(x):x是奇数,D(x,y):x除尽y.则 x(E(x)→D(x,y)→E(y》的汉语翻译为 6、设S={a,b,c)则S的集合表示为 7、P(P(Φ)= 8、A©B= 9、设R为集合A上的关系,则1(R)= 10、若R是集合A上的偏序关系,则R满足 二、选择20%(每小题2分) 1、下列命题正确的有()。 A、若g,∫是满射,则g°∫是满射:B、若g∫是满射,则g,∫都是满射: C、若gf是单射,则g,f都是单射:D、若gf单射,则f是单射。 2、设£,g是函数,当( )时,g。 A、x∈domf都有fx)=g(x):B、domg domf且fsg: C、与g的表达式相同: D.domg=domf,rangef=rangef 3、下列关系,( )能构成函数。 A、f={Kx,x2x,为2∈N且x+x2=10: B、={Kx,x2x1,x2∈R,1=x22} C、f=Kx,x2x,x2eN,为小于x的素数的个数}: 6
离散数学试卷(十一) 68 一、 填空 20% (每小题 2 分) 1、 称为命题。 2、命题 P→Q 的真值为 0,当且仅当 。 3、一个命题含有 4 个原子命题,则对其所有可能赋值有 种。 4、所有小项的析取式为 。 5、令 P(x):x 是质数,E(x):x 是偶数,Q(x):x 是奇数,D(x,y):x 除尽 y. 则 x(E(x) → y(D(x, y) → E( y))) 的汉语翻译为 。 6、设 S={a,b, c} 则 S6 的集合表示为 。 7、P(P( ))= 。 8、 A B = 。 9、设 R 为集合 A 上的关系,则 t(R)= 。 10、若 R 是集合 A 上的偏序关系,则 R 满足 。 二、 选择 20% (每小题 2 分) 1、 下列命题正确的有( )。 A、 若 g, f 是满射,则 g f 是满射; B、若 g f 是满射,则 g, f 都是满射; C、若 g f 是单射,则 g, f 都是单射;D、若 g f 单射,则 f 是单射。 2、 设 f,g 是函数,当( )时,f=g 。 A、xdomf 都有 f (x) = g(x) ; B、 domg domf 且 f g ; C、 f与g的表达式相同 ; D、 domg = domf ,rangef = rangef 。 3、 下列关系,( )能构成函数。 A、 { , | , 10} f = x1 x2 x1 x2 N且x1 + x2 = ; B、 { , | , , } 2 1 2 1 2 1 2 f = x x x x R x = x ; C、 { , | , , } f = x1 x2 x1 x2 N x2为小于x1的素数的个数 ;
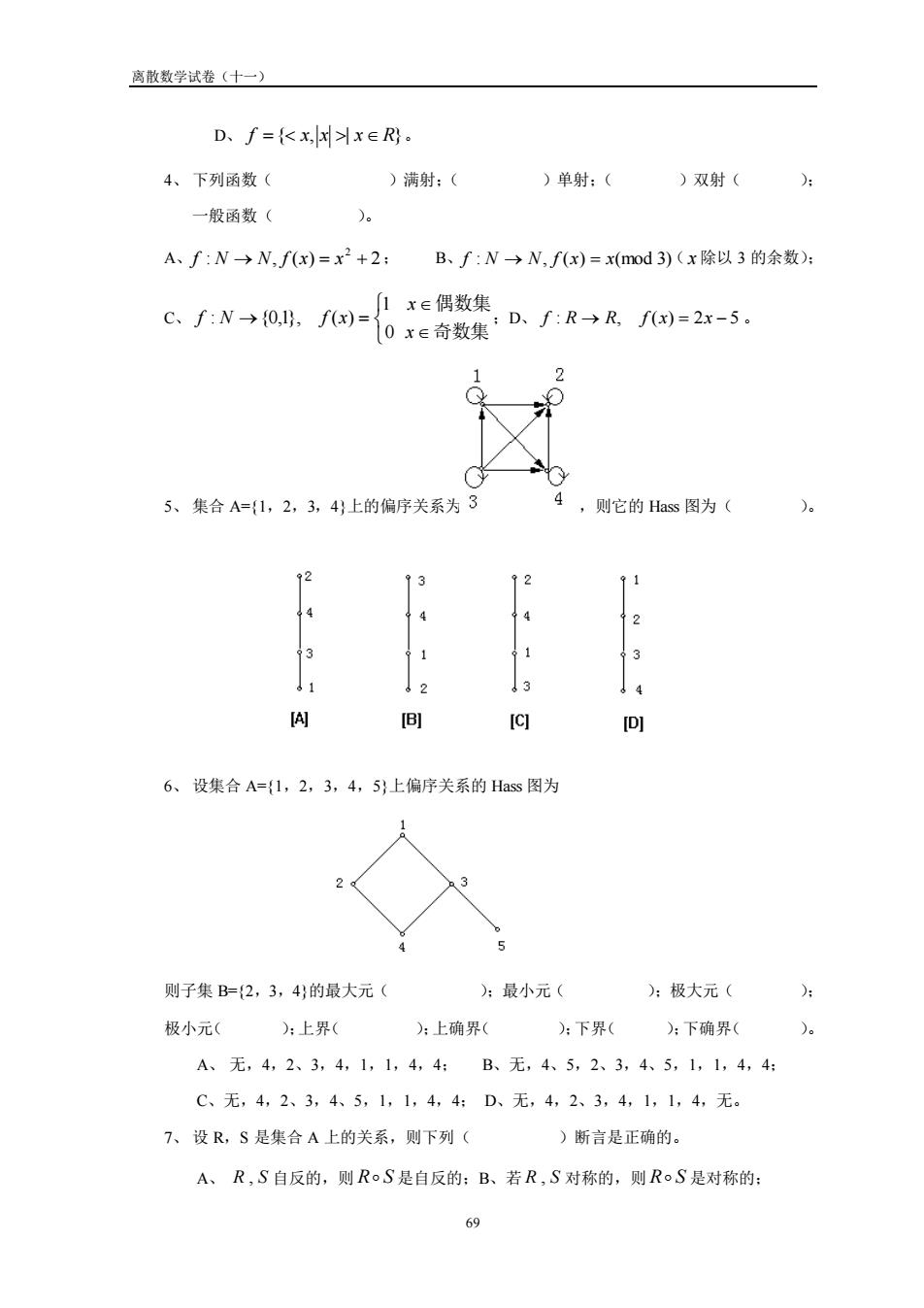
离散数学试卷(十一) D、f={kxx∈R. 4、下列函数( )满射:( )单射:()双射( 一般函数( A、f:N→N,fx)=x2+2:B、f:N→N,fx)=x(mod3)(x除以3的余数): 1x∈偶数集 Cf→0.=0数集D、/R→=2-5 5、集合A=1,2,3,4上的偏序关系为3 4,则它的Has图为( 13 92 1 2 3 向 IC] 6、设集合A={1,2,3,4,5}上偏序关系的Has图为 则子集B={2,3,4)的最大元( ):最小元( ):极大元( 极小元( ):上界( :上确界( ):下界():下确界( A、无,4,2、3,4,1,1,4,4:B、无,4、5,2、3,4、5,1,1,4,4: C、无,4,2、3,4、5,1,1,4,4:D、无,4,2、34,1,1,4,无. 7、设R,S是集合A上的关系,则下列( )断言是正确的。 A、R,S自反的,则RoS是自反的:B、若R,S对称的,则R。S是对称的: 69
离散数学试卷(十一) 69 D、 f ={ x, x | x R}。 4、 下列函数( )满射;( )单射;( )双射( ); 一般函数( )。 A、 : , ( ) 2 2 f N → N f x = x + ; B、f : N → N, f (x) = x(mod 3) ( x 除以 3 的余数); C、 → = 奇数集 偶数集 x x f N f x 0 1 : {0,1}, ( ) ;D、 f : R → R, f (x) = 2x − 5 。 5、 集合 A={1,2,3,4}上的偏序关系为 ,则它的 Hass 图为( )。 6、 设集合 A={1,2,3,4,5}上偏序关系的 Hass 图为 则子集 B={2,3,4}的最大元( );最小元( );极大元( ); 极小元( );上界( );上确界( );下界( );下确界( )。 A、 无,4,2、3,4,1,1,4,4; B、无,4、5,2、3,4、5,1,1,4,4; C、无,4,2、3,4、5,1,1,4,4; D、无,4,2、3,4,1,1,4,无。 7、 设 R,S 是集合 A 上的关系,则下列( )断言是正确的。 A、 R , S 自反的,则 R S 是自反的;B、若 R , S 对称的,则 R S 是对称的;

离散数学试卷(十一) C、若R,S传递的,则R。S是传递的:D、若R,S反对称的,则R。S是反对称的 8、设X为集合,X=n,在X上有( )种不同的关系。 A、2:B、2: C、2”:D、2。 9、下列推导错在( ①xa(x>y) ②3y(:>y) USO ③(e>C.) ES② ④x(x>x) UG③ A、②:B、③:C、④:D、无 10、“没有不犯错误的人”的逻辑符号化为( 设H(x:x是人,P(x):x犯错误。 A、3x(H(x)→Px):B、-(3x(H(x)APx)》: C、(3x(H(x)→Px)):D、xH(x)→P(x)。 三、命题演绎28% 1、(I0分)用反证法证明(PVQ)A(P→R)A(但→S)→SVR。 2、(8分)用CP规则证明P→(Q→R),R→(Q→S)一P→(Q→S)。 3、(10分)演绎推理:所有的有理数都是实数,所有的无理数也是实数,虚数不是实数。因此, 虚数既不是有理数,也不是无理数。 四、8% 将wf3x(一(yP(x,y》→(Q()→R(x)》化为与其等价的前束范式。 五、8% A={ab,cd,R={<ab>,<b,c心,<b,d,<c,b>为A上的关系,利用矩阵乘法求R的传递闭包,并画 出t(R)的关系图。 0
离散数学试卷(十一) 70 C、若 R , S 传递的,则 R S 是传递的;D、若 R , S 反对称的,则 R S 是反对称的 8、 设 X 为集合,|X|=n,在 X 上有( )种不同的关系。 A、n 2 ; B、2 n; C、 n 2 2 ; D、 2 2 n 。 9、 下列推导错在( )。 ① xy(x y) P ② y(z y) US① ③ ( ) Cz z ES② ④ x(x x) UG③ A、②; B、③; C、④; D、无。 10、“没有不犯错误的人”的逻辑符号化为( )。 设 H(x):x 是人, P(x):x 犯错误。 A、 x(H(x) → P(x)) ; B、(x(H(x) P(x))) ; C、 (x(H(x) → P(x))) ; D、x(H(x) → P(x)) 。 三、 命题演绎 28% 1、(10 分)用反证法证明 (P Q) (P → R) (Q → S) S R 。 2、(8 分)用 CP 规则证明 P → (Q → R), R → (Q → S) P → (Q → S) 。 3、(10 分)演绎推理:所有的有理数都是实数,所有的无理数也是实数,虚数不是实数。因此, 虚数既不是有理数,也不是无理数。 四、 8% 将 wff x((yP(x, y)) → (zQ(z) → R(x))) 化为与其等价的前束范式。 五、8% A={a,b,c,d},R={<a,b>,<b,c>,<b,d>,<c,b>}为 A 上的关系,利用矩阵乘法求 R 的传递闭包,并画 出 t(R)的关系图

离散数学试卷(十一) 六、证明16% 1、(8分)设A={1,2,3,4,在P(A)上规定二元关系如下: R=<s,t>5,tE P(A)A(sHD)) 证明R是P(A)上的等价关系并写出商集P(A)R。 2、(8分)设f是A到A的满射,且∫∫=∫,证明
离散数学试卷(十一) 71 六、证明 16% 1、 (8 分)设 A={1,2,3,4},在 P(A)上规定二元关系如下: R = { s,t | s,t P(A) (| s |=| t |)} 证明 R 是 P(A)上的等价关系并写出商集 P(A)/R。 2、 (8 分)设 f 是 A 到 A 的满射,且 f f = f ,证明 f=IA