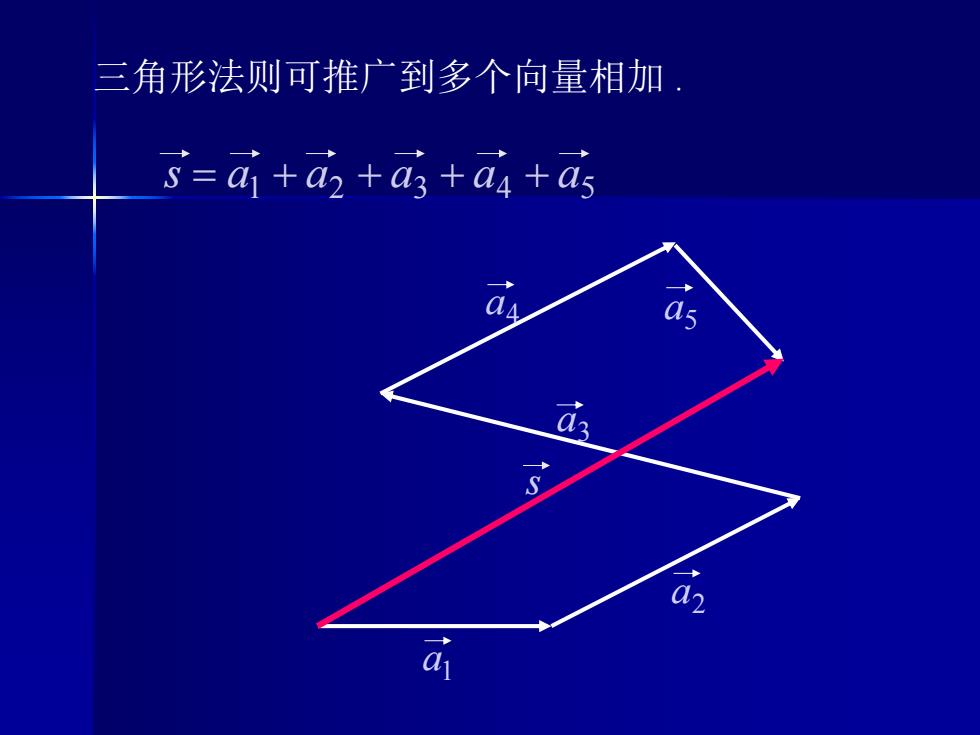
三角形法则可推广到多个向量相加 S-a+a2 +as+asas
s 3 a 4 a 5 a 2 a 1a 1 2 3 4 5 s a a a a a 三角形法则可推广到多个向量相加

2.向量的减法 b-a-b+(-@) b-a 三角不等式 a+bs a+B a-b s a+b
三角不等式 b a b (a ) a b a b b a a b b a a a b a b

3.向量与数的乘法 久是一个数,入与a的乘积是一个新向量,记作2ā. 规定:2>0时,元a与a同向,入a=2a: 2<0时,元a与a反向,2a=-2ag 2=0时,2a=0 注 1.a与a平行 2.a=2a 运算律:结合律2(u)=u(2)=2ua 分配律 (2+a=入a+ud
2. a a 是一个数 , a . 规定 : 0时, a与a同向, 0时, 0时, 0 . a a a ; a a ; 与 a 的乘积是一个新向量, 记作 a与a 反向, 注: 运算律 : 结合律 ( a) ( a) a 分配律 a ( ) a a a与 a平行 1.

若a≠0, a-aa 因此,单位向量 °= a. 定理1.设d为非零向量,则 a∥b =方=2a ()为唯一实数)
设 a 为非零向量 , 则 ( 为唯一实数) a∥b b a 0, 若a . 1 a a 因此,单位向量 a a a a

例1.设M为□ABCD对角线的交点,AB=a,AD=b 试用a与b表示MA,MB,MC,MD 解: a+b=AC b-a=BD M☑=-a+万)MB=-6-a) Mc=(a+bM远=(⑦-a)
例1. 设 M 为 M A B D C 解: ABCD 对角线的交点, b a AB a, AD b, AC BD 试用a 与b 表示 MA,MB,MC,MD. a b b a ( ) 2 1 MA a b ( ) 2 1 MB b a ( ) 2 1 MC a b ( ) 2 1 MD b a