
1 布尔代数
布尔代数 1

回顾 2 口内容1:代数格的定义与性质 口满足结合律、交换律、吸收律,亦可通过此三性质定义 代数格 ▣内容2:格同态、格同构 口格同态具有保序性,格同构的充要条件 口内容3:分配格、有补格、有补分配格 口分配格满足分配率(两个判定定理),有界格存在全上界 和全下届,有补格所有元素存在补元,有补分配格即布 尔代数
内容1:代数格的定义与性质 满足结合律、交换律、吸收律,亦可通过此三性质定义 代数格 内容2:格同态、格同构 格同态具有保序性,格同构的充要条件 内容3:分配格、有补格、有补分配格 分配格满足分配率(两个判定定理),有界格存在全上界 和全下届,有补格所有元素存在补元,有补分配格即布 尔代数 2 回顾

本节提要 3 口内容1:布尔代数 口内容2:有限布尔代数表示定理
内容1:布尔代数 内容2:有限布尔代数表示定理 3 本节提要

布尔代数的抽象定义 一个布尔代数是一个集合B,它有二元运算V和∧、 一元运算·以及特殊元素0和1,且B中元素满足下 列性质: 结合律 交换律 分配律 同一律 补律 (0,1,+,·,一,0,1)为布尔代数 口A的幂集构成一个布尔代数(p(A),U,∩,~,☑,A)
布尔代数的抽象定义 一个布尔代数是一个集合B,它有二元运算和、 一元运算 以及特殊元素0和1,且B中元素满足下 列性质: ({0, 1}, +, , , 0, 1)为布尔代数 A的幂集构成一个布尔代数((A), ⋃, ⋂, , ,A) 4 结合律 交换律 分配律 同一律 补律
布尔代数性质(1) 5 等式 名称 x+0y+z)=(x+y)+z 结合律 x0yz=(xy)·z x+(y-z)=(x+y)(x+z) 分配律 x.(y)xy+x. x+0=x 同一律 x1=x x+y=y+x 交换律 xy=yx x+x=1 补律 x·x=0
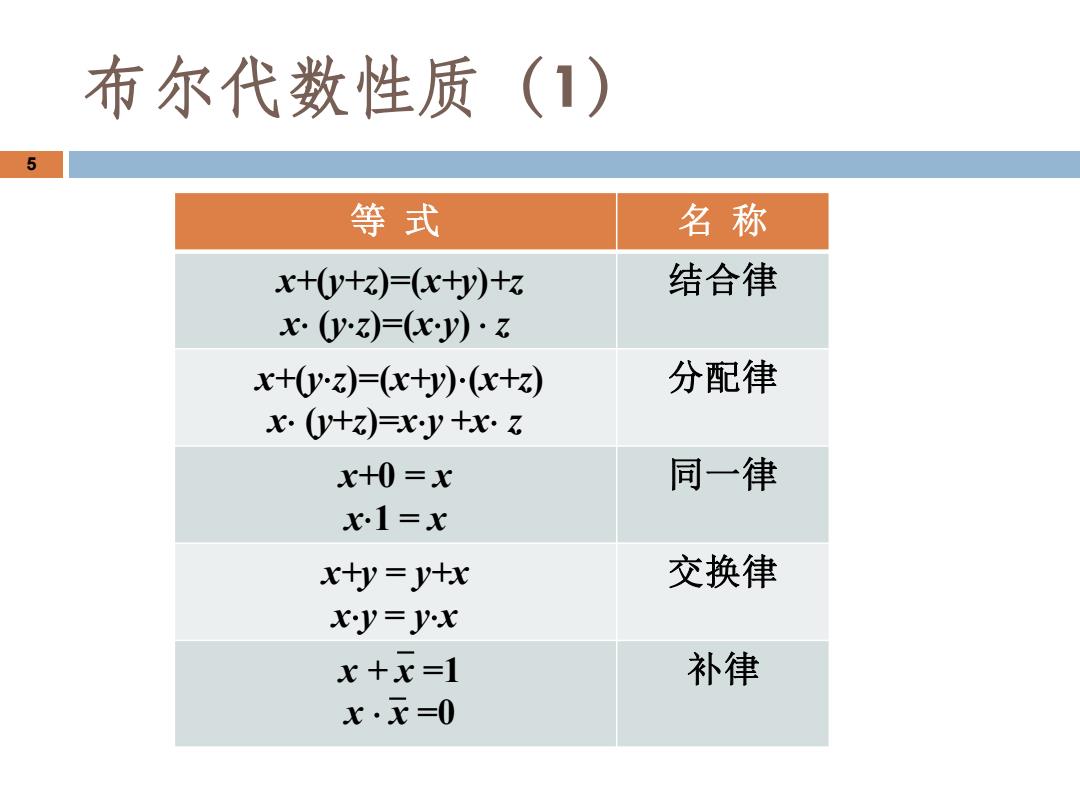
等 式 名 称 x+(y+z)=(x+y)+z x (yz)=(xy) z 结合律 x+(yz)=(x+y)(x+z) x (y+z)=xy +x z 分配律 x+0 = x x1 = x 同一律 x+y = y+x xy = yx 交换律 x + x =1 x x =0 补律 5 布尔代数性质(1)