
1 子群及其陪集
子群及其陪集 1

回顾 2 口问题1:什么是代数系统? 口非空集合+封闭的(二元)运算 口问题2:代数系统相关性质? 口封闭性、结合性、交换性、分配性;单位元、零元、逆 元;同态同构 口问题3:什么是群? 口封闭+结合律+单位元+逆元 口问题4:群具有哪些性质? ▣元素的阶、群的阶
回顾 问题1:什么是代数系统? 非空集合+封闭的(二元)运算 问题2:代数系统相关性质? 封闭性、结合性、交换性、分配性;单位元、零元、逆 元;同态同构 问题3:什么是群? 封闭 + 结合律 + 单位元 + 逆元 问题4:群具有哪些性质? 元素的阶、群的阶 2

本节提要 3 口问题1:什么是子群,如何判别之? ▣问题2:子群一定存在么,若存在则满足什 么性质?
本节提要 问题1:什么是子群,如何判别之? 问题2:子群一定存在么,若存在则满足什 么性质? 3

子群的定义 4 口设(G,o)是群,H是G的非空子集,如果H关于G中 的运算构成群,即(H,)也是群,则H是G的子群。 口记作(H,)≤(G,),简记为H≤G。 口例子:偶数加系统是整数加群的子群 o平凡子群(G,o),({e},o) 注意:结合律在G的子集上均成立
子群的定义 设(G, ⃘)是群,H是G的非空子集,如果H关于G中 的运算构成群,即(H, ⃘)也是群,则H是G的子群。 记作(H, ⃘) (G, ⃘), 简记为 HG。 例子:偶数加系统是整数加群的子群 平凡子群 (G, ⃘), ({e}, ⃘) 注意:结合律在G的子集上均成立。 4
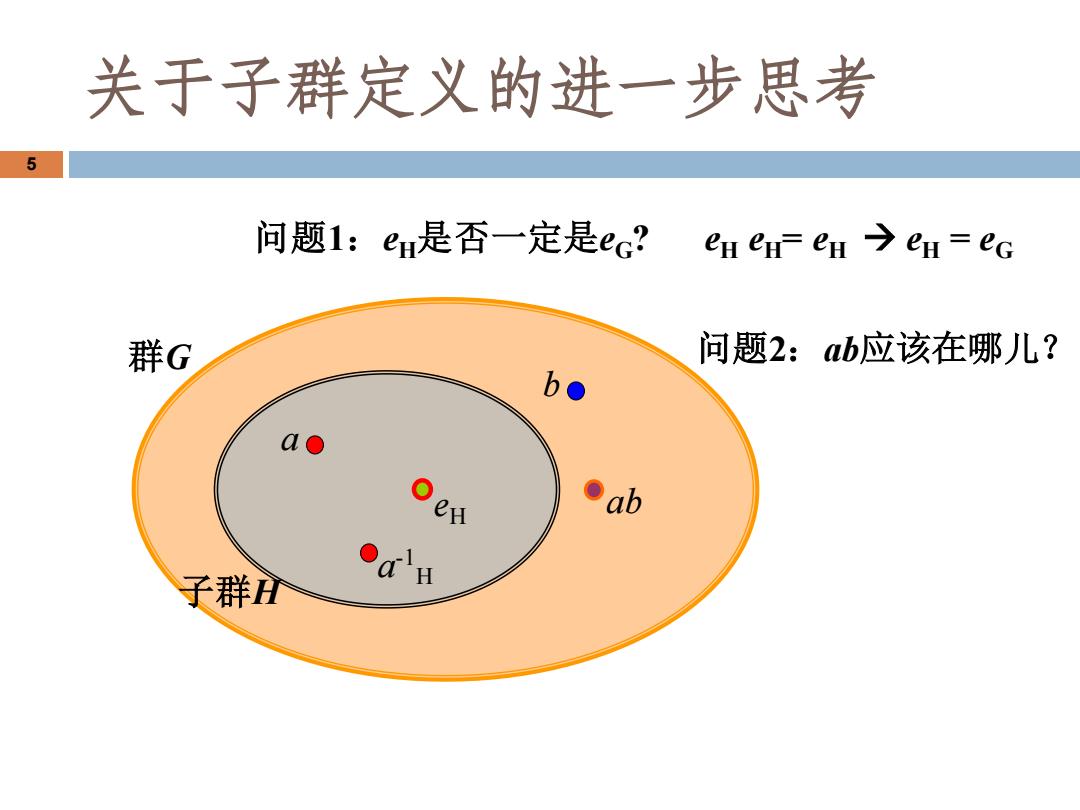
关于子群定义的进一步思考 5 问题1:eH是否一定是ec? en en=en→eH=eG 群G 问题2:ab应该在哪儿? b● ao 。w ab 子群A Oa'H
群G 子群H a b eH a -1 H 问题2:ab应该在哪儿? ab 问题1:eH是否一定是eG? eH eH = eH → eH = eG 5 关于子群定义的进一步思考