
1 关系的性质
关系的性质 1

回顾 口内容1:概率论 口概率函数、条件概率、独立性 口内容2:贝叶斯定理 a Pr[FIE]=P [EIF]Pr[F] Pr[E] 口内容3:随机变量及其期望与方差 口期望、条件期望、全期望公式(全概率公式)、期望的 线性性质、方差、概率化方法
内容1:概率论 概率函数、条件概率、独立性 内容2:贝叶斯定理 Pr 𝐹 𝐸 = Pr[𝐸∣𝐹] Pr 𝐹 Pr 𝐸 内容3:随机变量及其期望与方差 期望、条件期望、全期望公式(全概率公式)、期望的 线性性质、方差、概率化方法 回顾

本节提要 口问题1:关系具有哪些重要性质? 口问题2:如果计算关系的闭包?
问题1:关系具有哪些重要性质? 问题2:如果计算关系的闭包? 本节提要

关系的定义(回顾) 4 若A,B是集合,从A到B的一个关系是AxB的一个 子集。 口集合,可以是空集 口集合的元素是有序对 若A=B:称为“集合A上的(二元)关系
关系的定义(回顾) 若A, B是集合, 从A到B的一个关系是AB的一个 子集. 集合, 可以是空集 集合的元素是有序对 若A=B: 称为“集合A上的(二元)关系” 4
关系的表示(回顾) 5 假设A={a,b,c,d欧,B={%A,乃/1假设为有限集合 口集合表示:R1={(a月,(b,,(C,,(G)} 0-1矩阵 有向图 a B a 0 1 b 1 0 0 10 1 d 00 0 d A B
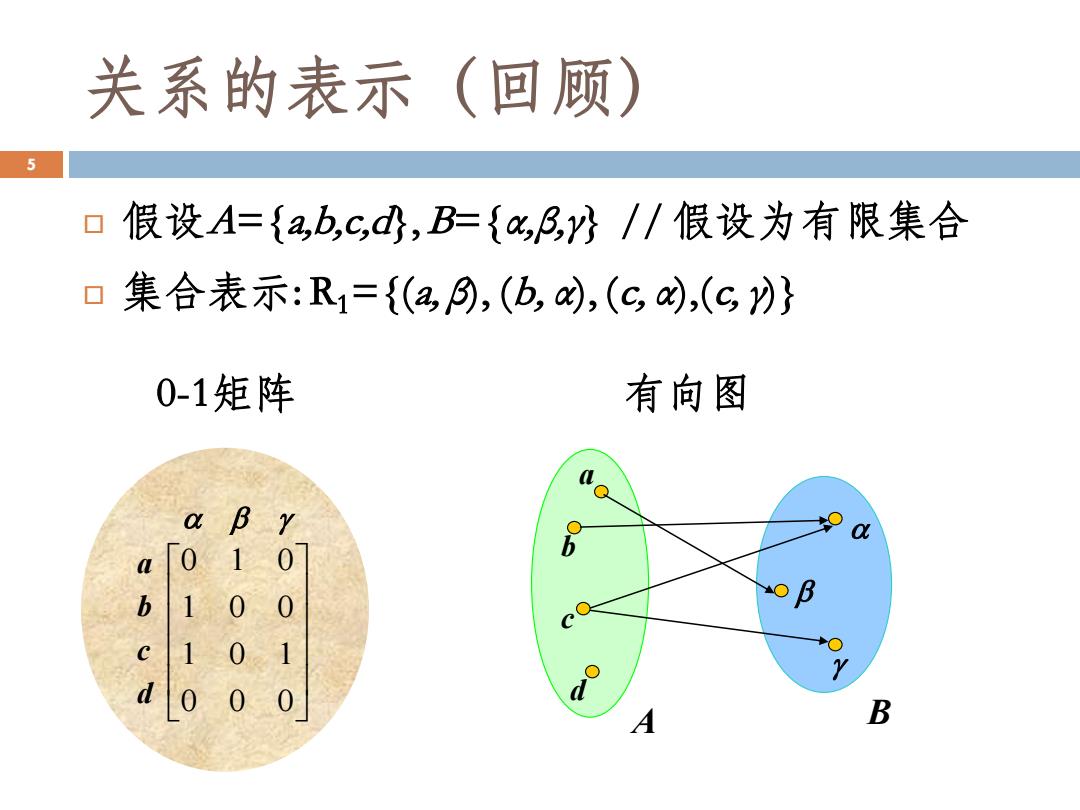
关系的表示(回顾) 假设A={a,b,c,d}, B={α,β,γ} // 假设为有限集合 集合表示: R1={(a, β), (b, α), (c, α),(c, γ)} 0-1矩阵 有向图 5 0 0 0 1 0 1 1 0 0 a 0 1 0 b c d a d c b A B