
1 几何概型
几何概型 1

几何概型 2 口早在概率论发展初期,人们就认识到,只考虑 有限个等可能样本点的古典方法是不够的。 ▣把等可能推广到无限个样本点场合,人们引入 了几何概型,由此形成了确定概率的另一方法: 几何方法
几何概型 早在概率论发展初期,人们就认识到,只考虑 有限个等可能样本点的古典方法是不够的。 把等可能推广到无限个样本点场合,人们引入 了几何概型,由此形成了确定概率的另一方法: 几何方法。 2

几何概型定义 3 设有一个可度量区域2(可以是1维,2维或3维区 域),向2内任意投点M,M落于2内任一点等可 能,且落在Ω内任何子区域A内上的可能性与A的 测度成正比,而与A的位置和形状无关,则称该 试验为几何概型试验,定义M落在A中的概率为 P(A)= A的几何测度 (A) Ω的几何测度 u(2) 口特点 ▣无限性:样本空间无限 口等可能性:每个样本点发生的可能性相同
几何概型定义 设有一个可度量区域𝛀(可以是1维,2维或3维区 域),向𝛀内任意投点𝑴,𝑴落于𝛀内任一点等可 能,且落在𝛀内任何子区域𝑨内上的可能性与𝑨的 测度成正比,而与𝑨的位置和形状无关,则称该 试验为几何概型试验,定义𝑴落在𝑨中的概率为 𝑷 𝑨 = 𝑨的几何测度 𝛀的几何测度 = 𝝁(𝑨) 𝝁(𝛀) 特点 无限性:样本空间无限 等可能性:每个样本点发生的可能性相同 3
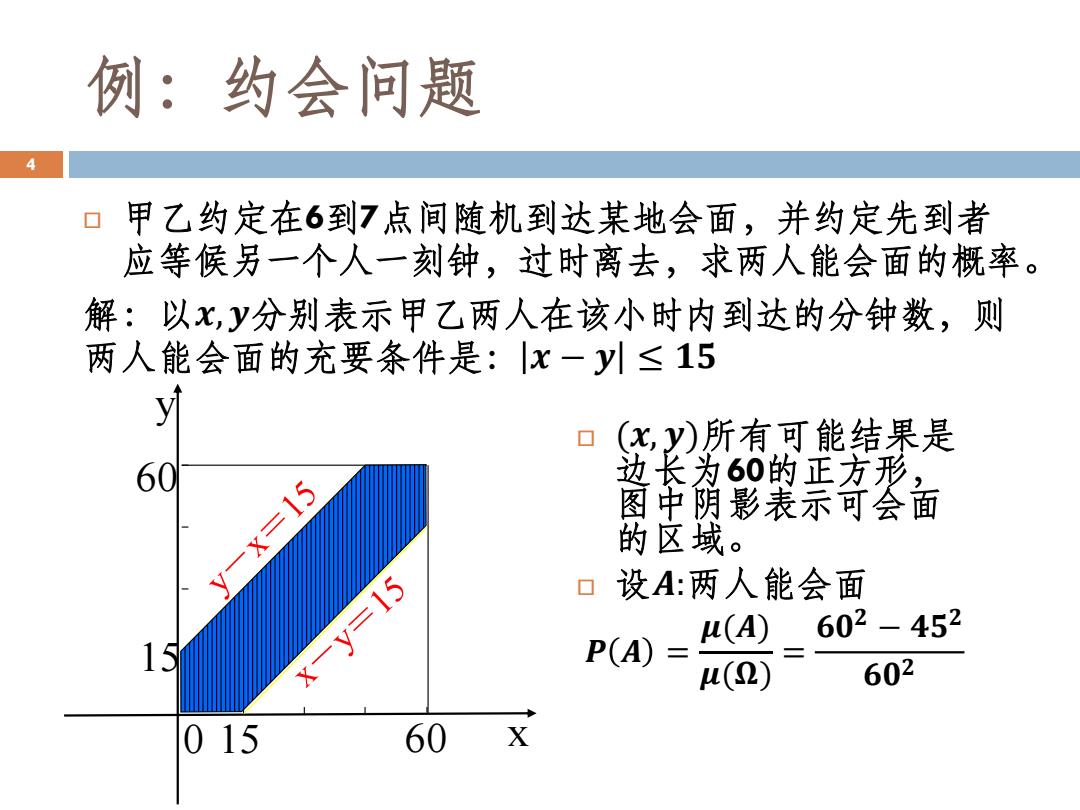
例:约会问题 4 甲乙约定在6到7点间随机到达某地会面,并约定先到者 应等候另一个人一刻钟,过时离去,求两人能会面的概率。 解:以x,y分别表示甲乙两人在该小时内到达的分钟数,则 两人能会面的充要条件是:|x-y川≤15 (x,y)所有可能结果是 60 边长为60的正方形, y-x=15 图中阴影表示可会面 的区域。 设A:两人能会面 x-y=15 602-452 15 P(A) (A) u(2) 602 015 60 X
例:约会问题 甲乙约定在6到7点间随机到达某地会面,并约定先到者 应等候另一个人一刻钟,过时离去,求两人能会面的概率。 解:以𝒙,𝒚分别表示甲乙两人在该小时内到达的分钟数,则 两人能会面的充要条件是: 𝒙 − 𝒚 ≤ 𝟏𝟓 4 0 15 15 60 60 y x (𝒙, 𝒚)所有可能结果是 边长为60的正方形, 图中阴影表示可会面 的区域。 设𝑨:两人能会面 𝑷 𝑨 = 𝝁(𝑨) 𝝁(𝛀) = 𝟔𝟎 𝟐 − 𝟒𝟓 𝟐 𝟔𝟎 𝟐
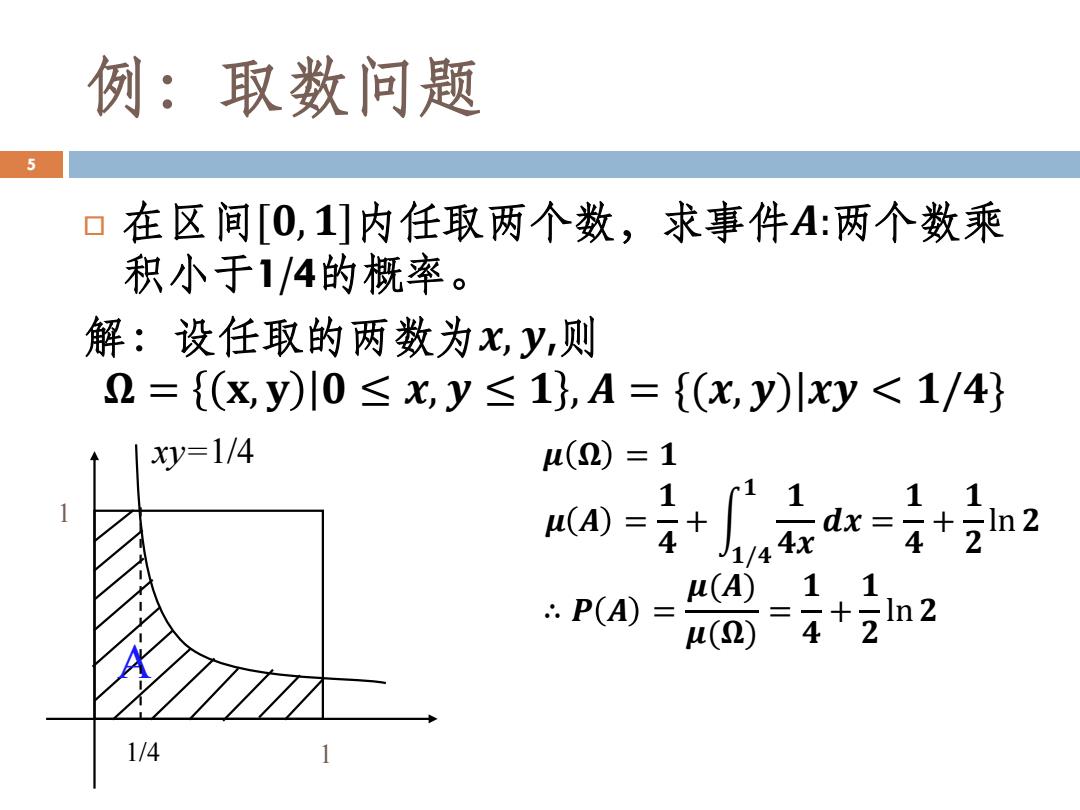
例:取数问题 5 在区间[0,1]内任取两个数,求事件A:两个数乘 积小于1/4的概率。 解:设任取的两数为X,y,则 2={(x,y)I0≤x,y≤1,A={(x,y)川xy<1/4 xy=1/4 u(2)=1 1 u(A)= 1/4 P(A)= (A) u(2) =4 2n2 1/4
例:取数问题 在区间[𝟎, 𝟏]内任取两个数,求事件𝑨:两个数乘 积小于1/4的概率。 解:设任取的两数为𝒙, 𝒚,则 𝛀 = 𝐱, 𝐲 𝟎 ≤ 𝒙, 𝒚 ≤ 𝟏 , 𝑨 = {(𝒙, 𝒚)|𝒙𝒚 < 𝟏/𝟒} 5 xy=1/4 1 1 A 1/4 𝝁 𝛀 = 𝟏 𝝁 𝑨 = 𝟏 𝟒 + න 𝟏/𝟒 𝟏 𝟏 𝟒𝒙 𝒅𝒙 = 𝟏 𝟒 + 𝟏 𝟐 ln 𝟐 ∴ 𝑷 𝑨 = 𝝁(𝑨) 𝝁(𝛀) = 𝟏 𝟒 + 𝟏 𝟐 ln 𝟐