南京大学：《离散数学》课程教学资源（PPT课件讲稿）Lecture 09 计数

1 计数

计数 1

本节提要 口内容1：容斥原理 口内容2：鸽笼原理 口内容3：排列与组合

 内容1：容斥原理  内容2：鸽笼原理  内容3：排列与组合 本节提要

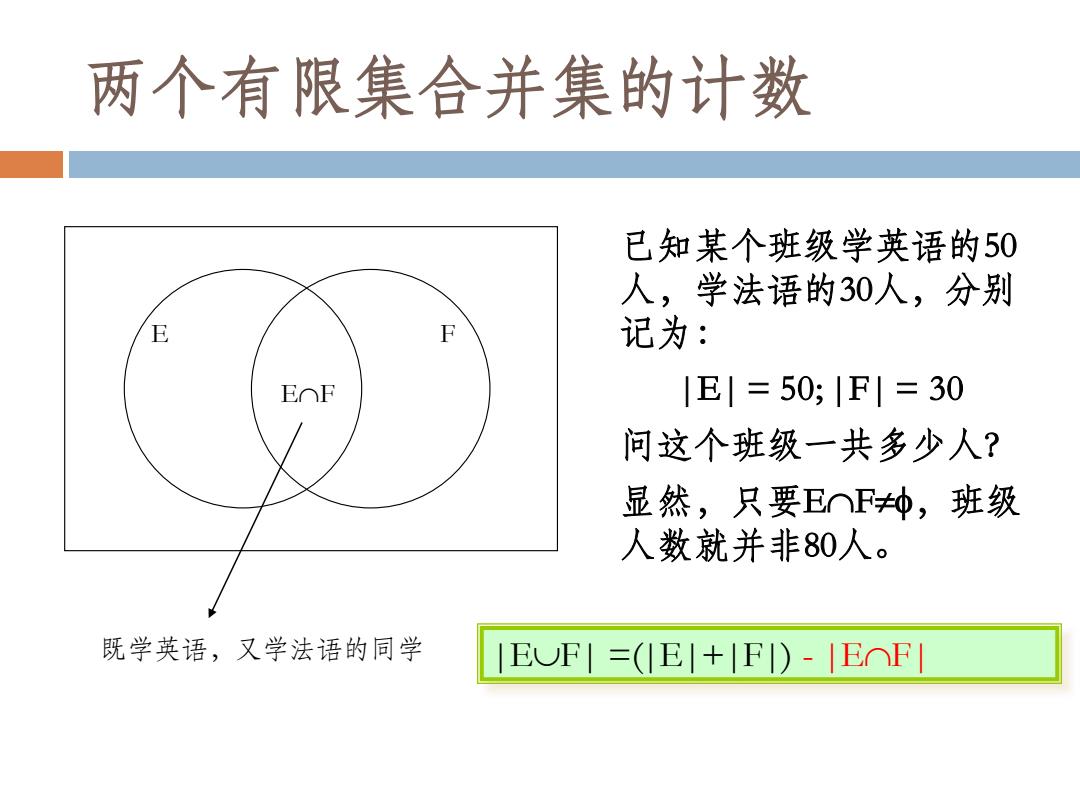
两个有限集合并集的计数 已知某个班级学英语的50 人，学法语的30人，分别 E 记为： E⌒F |E=50,1F|=30 问这个班级一共多少人？ 显然，只要E⌒F地，班级 人数就并非80人。 既学英语，又学法语的同学 EUF|=(IE|+|FI)-IE⌒F

两个有限集合并集的计数 既学英语，又学法语的同学 E F EF 已知某个班级学英语的50 人，学法语的30人，分别 记为： |E| = 50; |F| = 30 问这个班级一共多少人？ 显然，只要EF，班级 人数就并非80人。 |EF| =(|E|+|F|) - |EF|

数字排列的例子 将0,1,2，，9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？ 口这10个数字所有的排法构成全集U,|U1=10! 口第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法)， |A=29I 口最后一个数字不小于8的排法构成子集B(即所有以8或者9结束的 排法)，|B|=29列 ▣|A⌒B|=228! 口题目要求的排法构成子集(~A⌒~B) ▣I(~A⌒~B)1=IU|-IAUB|=IU|-|A|-|B|+IA∩B|=10I -4◆91+4◆81=2,338,560

数字排列的例子  将0,1,2,...,9排成一列，要求第1个数字大于1，最后一 个数字小于8，共有多少种排法？  这10个数字所有的排法构成全集U, |U|=10!  第1个数字不大于1的排法构成子集A(即所有以0或者1开头的排法), |A|=29!  最后一个数字不小于8的排法构成子集B(即所有以8或者9结束的 排法), |B|=29!  |AB|=228!  题目要求的排法构成子集(~A~B)  |(~A~B)| = |U| - |AB| = |U| -|A| - |B| + |AB| = 10! - 49! + 48! = 2,338,560

三个有限集合并集的计数 口假设定义全集的三个子集A,B,C。则： AUBOCI=|A|+IB|+|C-|A∩B|-IA⌒C-|B⌒CI+|A⌒B⌒CI 证明： IAUBUCI=AUB+CI-(AUB)OC =|A|+IB|-|A⌒B|+ICl-I(A⌒C)火UB⌒C)I =|A|+|B|-|A⌒B|+ICl-I(A⌒C)川-IB⌒C)|+I(A⌒B∽C)I =|A|+|B|+|C-|A⌒B|-|A⌒C-IB⌒C+|A⌒B∽C

三个有限集合并集的计数  假设定义全集的三个子集A,B,C。则： |ABC|=|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC| 证明： |ABC|=|AB|+|C|-|(AB)C| =|A|+|B|-|AB|+|C|-|(AC)(BC)| =|A|+|B|-|AB|+|C| - |(AC)|-|(BC)|+|(ABC)| =|A|+|B|+|C|-|AB|-|AC|-|BC|+|ABC|