
1 欧拉图与汉密尔顿图
欧拉图与汉密尔顿图 1

回顾 2 口内容1:通路与回路 口简单通路边不重复、初级通路点不重复 口内容2:无向图的连通性 口割点、割边,点/边连通度、K(G)≤入(G)≤δ(G), Whitney定理 口内容3:有向图的连通性 口强/单/弱连通,无向图的边定向
内容1:通路与回路 简单通路边不重复、初级通路点不重复 内容2:无向图的连通性 割点、割边,点/边连通度、(G) (G) (G), Whitney定理 内容3:有向图的连通性 强/单/弱连通,无向图的边定向 2 回顾

本节提要 口内容1:欧拉图 口什么是欧拉图? ▣欧拉图的充要条件? 口如何构造欧拉回路? ▣内容2:哈密尔顿图 口什么是汉密尔顿图? 口哈密尔顿图的必要和充分条件? 口哈密尔顿图有哪些应用?
内容1:欧拉图 什么是欧拉图? 欧拉图的充要条件? 如何构造欧拉回路? 内容2:哈密尔顿图 什么是汉密尔顿图? 哈密尔顿图的必要和充分条件? 哈密尔顿图有哪些应用? 本节提要
Kδnigsberg七桥问题(回顾) 4 K的NWGH莱U风 Leonhard Euler(1707-1783)
Königsberg七桥问题(回顾) 4 Leonhard Euler (1707 – 1783)
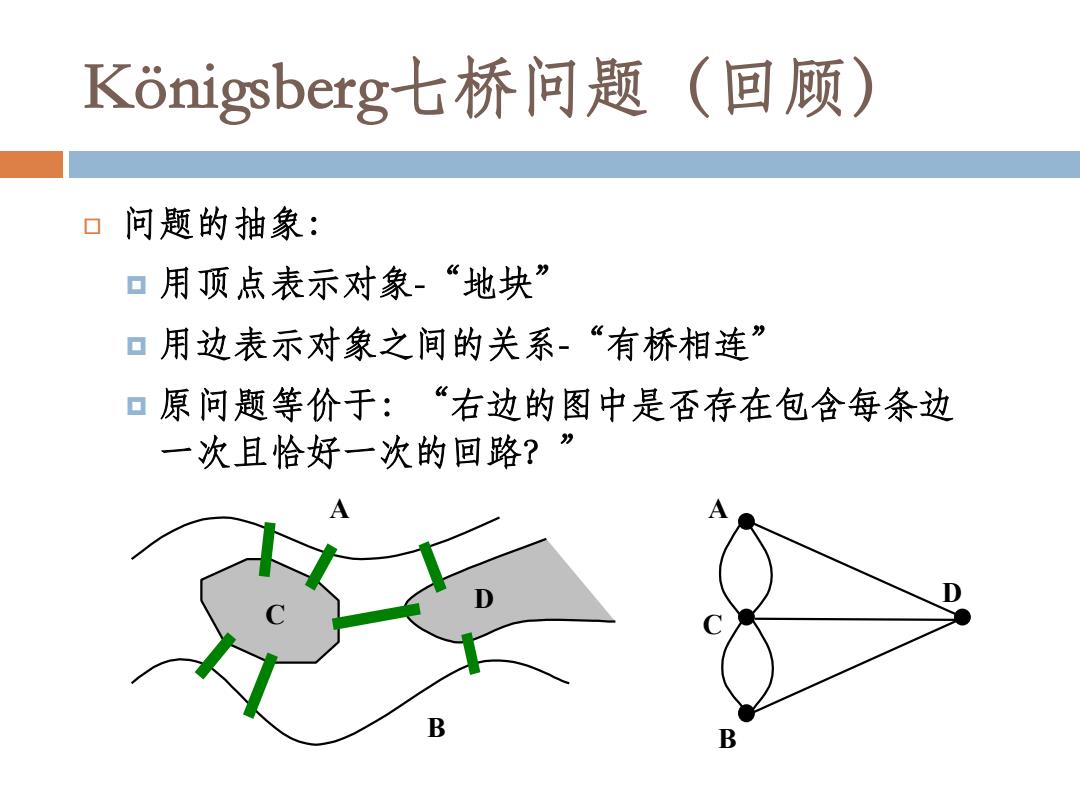
Kδnigsberg-七桥问题(回顾) 问题的抽象: 口用顶点表示对象“地块” 口用边表示对象之间的关系。“有桥相连” 口原问题等价于:“右边的图中是否存在包含每条边 一次且恰好一次的回路?” B
问题的抽象: 用顶点表示对象-“地块” 用边表示对象之间的关系-“有桥相连” 原问题等价于:“右边的图中是否存在包含每条边 一次且恰好一次的回路?” C D A B A C B D Königsberg七桥问题(回顾)