
1 图论-基本概念
图论 - 基本概念 1

回顾 2 口内容1:布尔代数 口满足结合、分配、同一、交换、补律;有补分配格 口内容2:有限布尔代数表示定理 口任意布尔代数同构于其原子构成集合的幂集代数系统
内容1:布尔代数 满足结合、分配、同一、交换、补律;有补分配格 内容2:有限布尔代数表示定理 任意布尔代数同构于其原子构成集合的幂集代数系统 2 回顾

本节提要 3 口内容1:图的定义 ▣内容2:图的应用 口内容3:图的表示 ▣内容4:图的同构
本节提要 内容1:图的定义 内容2:图的应用 内容3:图的表示 内容4:图的同构 3
图的定义Graph 常常省略,写作: 4 G=(V,E) 图G是一个三元组:G=(V,E, 口V是非空顶点集,E是边集,且V∩E=; 口p:E→P),且Ve∈E.1≤|go(e)≤2.p(e)称为边e的端点集. 口举例(数据中心、通信链接) 底特律 纽约 旧金山 丹佛 芝加哥 华盛顿 洛杉矶
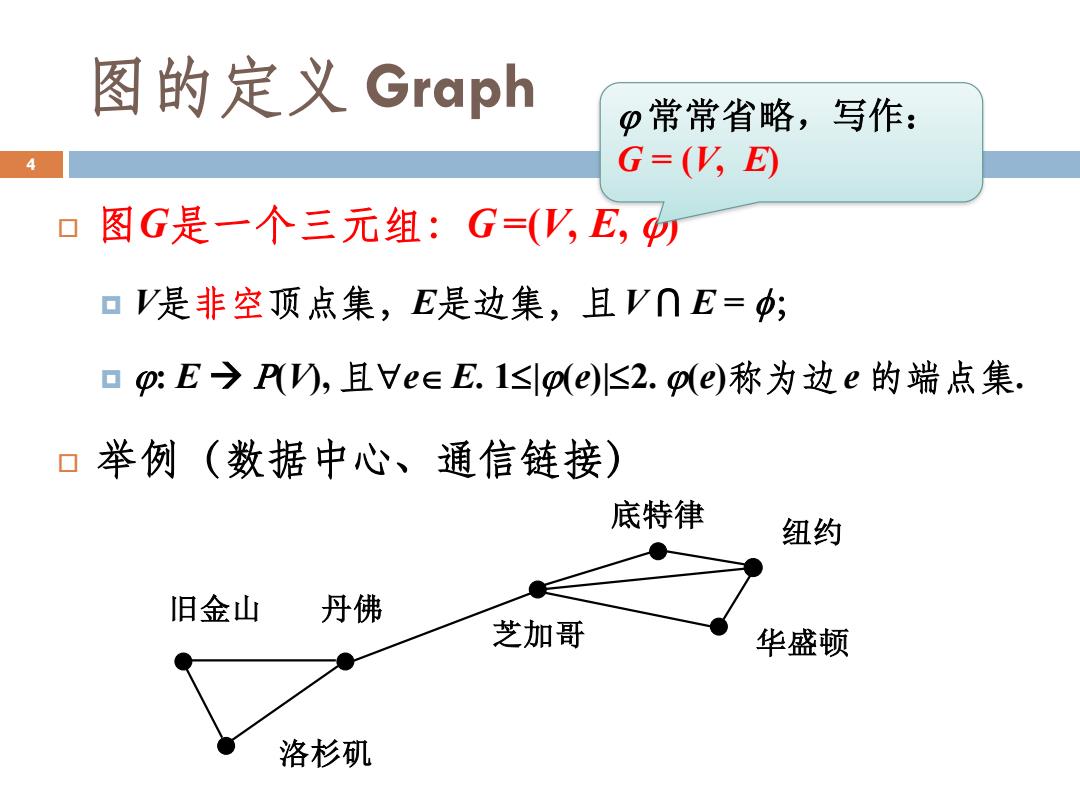
图的定义 Graph 图G是一个三元组:G =(V, E, ) V是非空顶点集,E是边集,且V ⋂ E = ; : E → (V), 且e E. 1|(e)|2. (e)称为边e 的端点集. 举例(数据中心、通信链接) 洛杉矶 旧金山 丹佛 芝加哥 华盛顿 纽约 底特律 常常省略,写作: 4 G = (V, E)

图的定义(续) 5 图G=(V,E,p)是简单图,如果 口每条边有2个端点,即:e∈E.lp(e)川=2,并且 口不同边有不同端点集,即:如果e1≠e2,则p(ei)≠p(e2) 口图G=(V,E,p)是伪图,如果 口存在一条只有1个端点的边,即:3eo∈E.lp(eo)川=1,或者 口有两条边具有相同的端点集,即:3e1≠e2p(e1)=p(c2)
图的定义(续) 图G = (V, E, )是简单图,如果 每条边有2个端点,即:e E. |(e)| = 2,并且 不同边有不同端点集,即:如果e1 e2 ,则(e1 ) (e2 ) 图G = (V, E, )是伪图,如果 存在一条只有1个端点的边,即: e0E.|(e0 )| = 1,或者 有两条边具有相同的端点集,即: e1 e2 .(e1 )=(e2 ) 5