《自动控制原理》课程教学资源（PPT课件）第四章 线性控制系统的动静态分析

3.4二阶系统的时域分析2.00F1.801.60 .31.402120.11.000.80.60.40210-1204911123581067t/r二阶系统的单位阶跃响应曲线

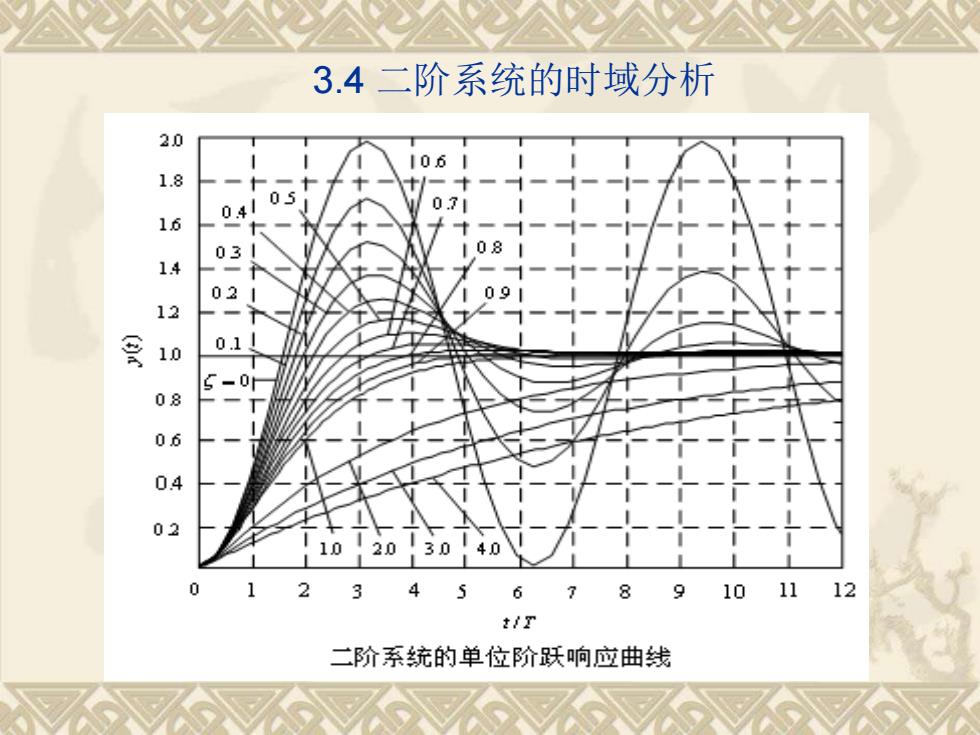
3.4 二阶系统的时域分析

3.4二阶系统的时域分析与一阶系统单位阶跃响应曲线比较，有两个特点：（1）响应曲线在初始时刻的导数为零。O,sinw,t, 5=0, t≥00.5=000,e-5 sinat, 0<5<1, t≥00<5<1dy(t)V1-52dy(t)dt0,5=1t=0o'te-, 5=1, t≥0dt0,5>1-(5-152-10t+25>1,，t≥0?2.01.8（2）响应曲线在初始上升阶段16二阶导数先递增后递减，出现一阶系统单位阶跃响应曲线没有的拐点现象，见图。0.4111012:86S2/1二阶系统的单位阶跃响应曲线

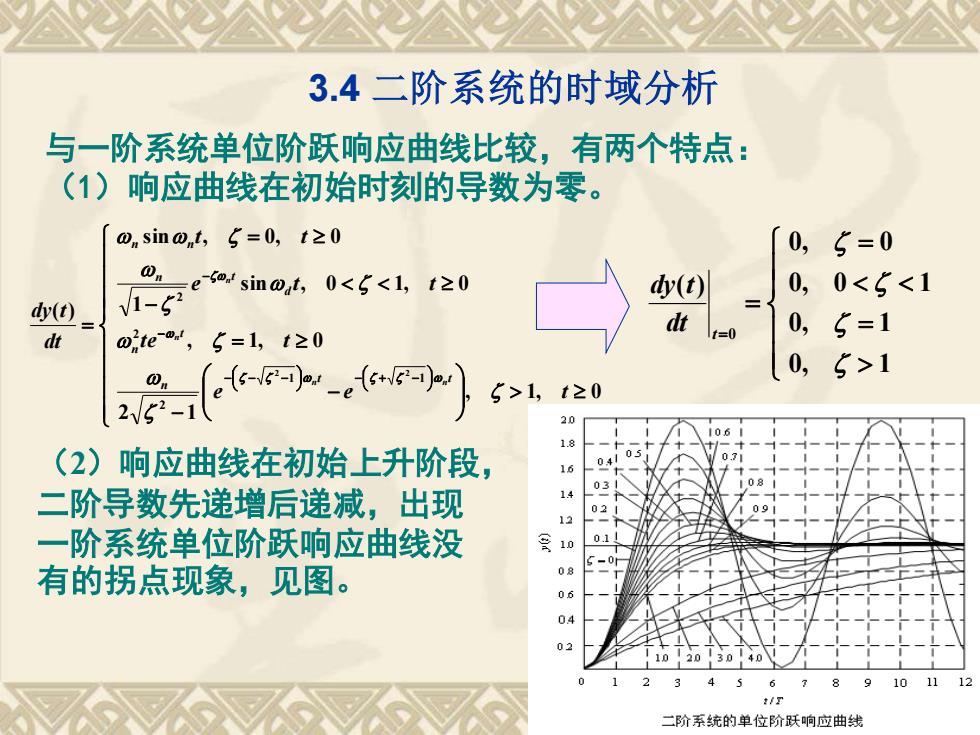
3.4 二阶系统的时域分析 与一阶系统单位阶跃响应曲线比较，有两个特点： （1）响应曲线在初始时刻的导数为零。                      − − =     − =  =        − + −      − − − − − , 1, 0 2 1 , 1, 0 sin , 0 1, 0 1 sin , 0, 0 ( ) 1 1 2 2 2 2 2 e e t t e t e t t t t dt dy t t t n t n d n t n n n n n n                              =   = = = 0, 1 0, 1 0, 0 1 0, 0 ( ) 0     t dt dy t （2）响应曲线在初始上升阶段， 二阶导数先递增后递减，出现 一阶系统单位阶跃响应曲线没 有的拐点现象，见图

2.01.8153.4二阶系统的时域分析1 412响应曲线的二阶导数为O0.11 008o, coso,t, 5=0, t≥000020.4=e-o" sin(oat-β), 0<5<1, t≥01-202d"y(t)(1-o,t)o,e-, 5=1, t≥02126810dt?IT0二阶系统的单位阶跃响应曲线>1, t≥0 (3-21)2V52-1++d'y(t)=0可求得响应曲线在初始上升阶段的拐点时间为：dt?元5=020综上，二阶系统单位阶跃响应：β1）当≥1时，响应单调上升0<5<1Od2）当0<<1时，响应为衰减振(3-22)tg=1S=1荡；On3）当=0时，等幅振荡；2-1)-In(-In(+y4）当<0时，两个具有正实部2.0的极点，不稳定

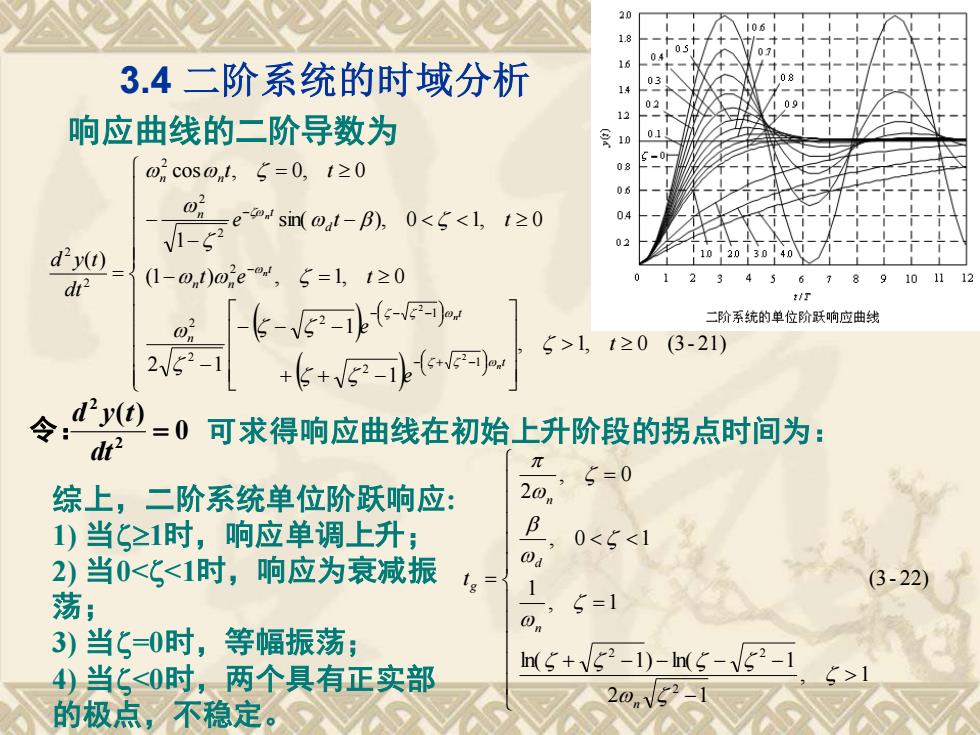
(3 - 22) , 1 2 1 ln( 1) ln( 1 , 1 1 , 0 1 , 0 2 2 2 2               − + − − − − =   = =                n n d n g t 3.4 二阶系统的时域分析 综上，二阶系统单位阶跃响应: 1) 当1时，响应单调上升； 2) 当0<<1时，响应为衰减振 荡； 3) 当=0时，等幅振荡； 4) 当<0时，两个具有正实部 的极点，不稳定。( )  ( )                         + + − − − − − − =  −    − − =  =       − + −       − − − − − , 1, 0 (3- 21) 1 1 2 1 (1 ) , 1, 0 sin( ), 0 1, 0 1 cos , 0, 0 ( ) 1 2 1 2 2 2 2 2 2 2 2 2 2 2 t e e t e t e t t t t dt d y t t t n t n n d n t n n n n n n                           0 ( ) 2 2 = dt d y t 令： 响应曲线的二阶导数为 可求得响应曲线在初始上升阶段的拐点时间为：

3.4二阶系统的时域分析3.4.3二阶系统单位阶跃响应的性能指标r1、欠阻尼情况jwr-(1)上升时间t：：以t）=1,即Cont,3sin(at, +β)=1 (3 -23)02Lu,:.0at,+β=元5?元-β元-β(4 - 24)On/1-2Qd1-2β= arccos5 = arcsin V1-2阻尼角=arctan

3.4 二阶系统的时域分析 3.4.3 二阶系统单位阶跃响应的性能指标 sin( ) (3 - 23) 1 (1) 2 1 1 上升时间 ： ( ) 1 ,即 + = − − = − ω t β e t y t d r ω t r r n r    (4 - 24) 1 2 −  − = − =  + = n d r d r ω π β ω π β t ω t β π ,阻尼角 1 arccos arcsin 1 arctan 2 2      − = = − = 1、欠阻尼情况

(2)峰值时间，：(t)第一次出现峰的时间dy(t)=0dtt=t1-*p sin( Oat, + β)+Oge-0*p cos(at, +β)]=0 (3-25)Co.eJ(t)/1-5matan(at, +β):(0)= tan β(3-26)5y(oo)のat,=k元, k=0,1,2,...(3-27)元(3-28)

(2)峰值时间t p : y(t)第一次出现峰值的时间。 tan (3- 26) 1 tan( ) 2      = − d t p + = 0 ( ) = = p t t dt dy t [ sin( ) cos( )] 0 (3- 25) 1 1 2 − + + + = − − −          d p t d p d t n e t e t n p n p t = k , k = 0,1, 2,  (3- 27) d p  (3- 28) 1 2      − = = n d p t t y(t) 0 ( ) 2 1 y  y() max y  y() d t rt p t s t Mp