《自动控制原理》课程教学资源（PPT课件）第四章 线性控制系统的动静态分析

3.4二阶系统的时域分析3.4.1二阶系统的一般形式T2 d"y(l)dy(t)+2CTy(t)= Kr(t)(3-10)+dt?dtY(s)1(3-11)T?s? +2CTs +1R(s)OY(s)O(3-12)s?+260,s+0,R(s)-R(s)Y(s)on典型二阶控制系统的结构图s(s+2g0n)

3.4 二阶系统的时域分析 3.4.1 二阶系统的一般形式 ( ) ( ) (3-10) ( ) 2 ( ) 2 2 2 y t Kr t dt dy t T dt d y t T +  + = (3-11) 2 1 1 ( ) ( ) 2 2 + + = R s T s Ts Y s  (3-12) ( ) 2 ( ) 2 2 2 n n n R s s s Y s    + + = ( 2 ) 2 n n s s   + R(s) Y(s) 典型二阶控制系统的结构图

3.4二阶系统的时域分析3.4.2二阶系统的单位阶跃响应?Y(s) =R(s)$? +250,s+0,w,(3-13)s(s? +250,s+0))s+250Y..(s)+Y.(s)+20,s+00(t) = yss(t)+ y:(t) = Ls(s* +250,s+0)s+250= L-'[s,(s)+ Y(s)]= -L(3-14)+250,s+0第二项取决于阻尼系数$+250t≥0= 1-L和自然振荡角频率s2+250s+0

3.4 二阶系统的时域分析 3.4.2 二阶系统的单位阶跃响应 ( ) ( ) 2 1 2 ( 2 ) ( ) 2 ( ) 2 2 2 2 2 2 2 2 Y s Y s s s s s s s s R s s s Y s s s t n n n n n n n n n = + + + + = − + + = + + =                , 0 2 2 1 2 1 2 ( ) ( ) ( 2 ) ( ) ( ) ( ) 2 2 1 2 2 1 1 1 2 2 2 1        + + + = −       + + + −      = + =       + + = + = − − − − − t s s s L s s s L s L Y s Y s L s s s y t y t y t L n n n n n n s s t n n n s s t               第二项取决于阻尼系数 和自然振荡角频率 (3 -13) (3 -14)

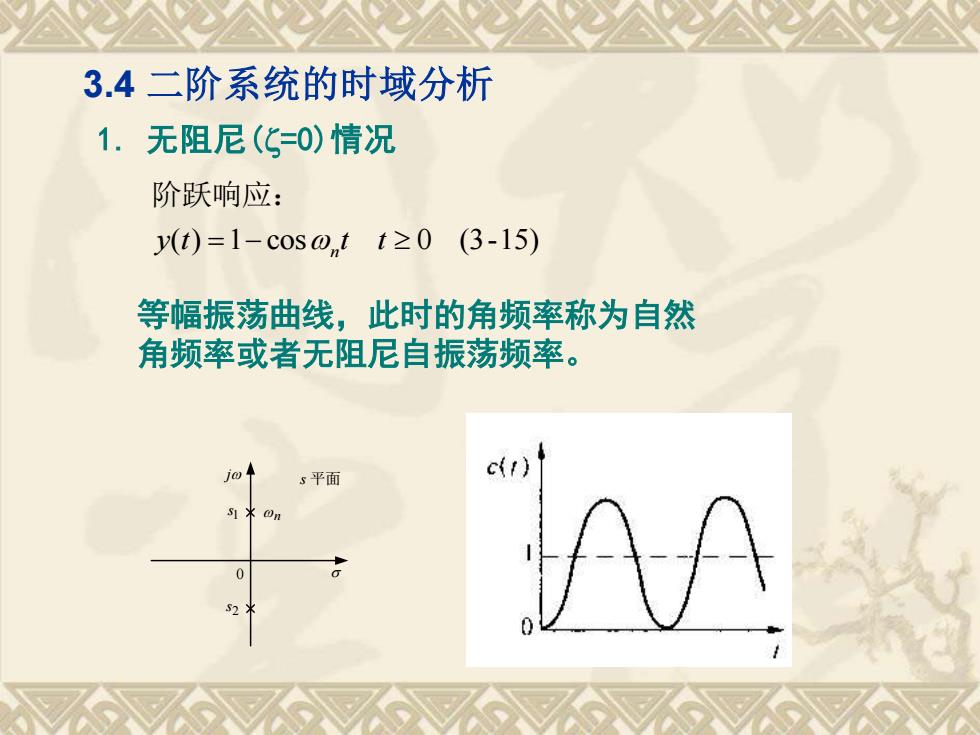
3.4二阶系统的时域分析1.无阻尼（C=0）情况阶跃响应：y(t)=1-cosの,t t≥0 (3-15)等幅振荡曲线，此时的角频率称为自然角频率或者无阻尼自振荡频率。10s平面SI*On0S2

3.4 二阶系统的时域分析 1. 无阻尼(=0)情况 y(t) =1− cos t t  0 (3-15) n 阶跃响应： 等幅振荡曲线，此时的角频率称为自然 角频率或者无阻尼自振荡频率。 j s 平面 0  1 s2 s n

3.4二阶系统的时域分析2.欠阻尼（0<<1）情况1e-(o" sin(@at+β), t≥0 (3-16)y(t)=1-Vi-g?のa=のV1-5，阻尼振荡角频率；β=arccos5,阻尼角1）稳态分量为1，瞬态分量为衰减的正弦jos平面振荡；od-on2）共轭复数极点实部的绝对值，决定了欠0阻尼响应的衰减速度，其数值越大，*-od共轭复数极点离虚轴就越远，欠阻尼S2响应衰减得越快。3）阻尼振荡角频率の.总是小于系统y(t)的自然振荡角频率のn。4）欠阻尼响应过程的偏差随时间的推移而减小

3.4 二阶系统的时域分析 2. 欠阻尼(0<<1)情况 sin ( ), 0 (3-16) 1 1 ( ) 1 2 +  − = − − y t e t t d t n     1) 稳态分量为1 ,瞬态分量为衰减的正弦 振荡; 2)共轭复数极点实部的绝对值,决定了欠 阻尼响应的衰减速度,其数值越大， 共轭复数极点离虚轴就越远，欠阻尼 响应衰减得越快。 3）阻尼振荡角频率d总是小于系统 的自然振荡角频率n。 4)欠阻尼响应过程的偏差随时间的推移 而减小。 d = n 1− 2 ，阻尼振荡角频率； = arccos  ,阻尼角j s 平面 0  1 s 2 s d −n −d y(t)

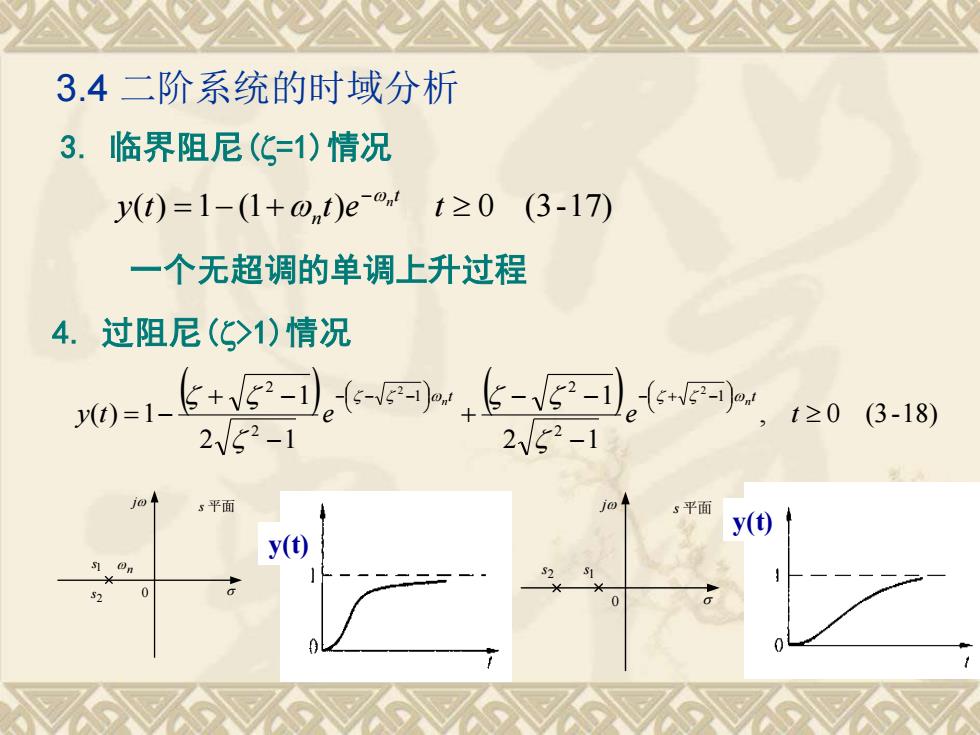
3.4二阶系统的时域分析3.临界阻尼（C=1）情况y(t) = 1-(1+の,t)e-ontt≥0(3-17)一个无超调的单调上升过程4.过阻尼（C>1）情况5+v52y(t)= 1t≥0 (3-18)2/21jos平面jos平面y(t)y(t)S1D0S2

3.4 二阶系统的时域分析 3. 临界阻尼(=1)情况 ( ) =1− (1+ )  0 (3-17) − y t t e t t n  n 一个无超调的单调上升过程 4. 过阻尼(>1)情况 ( ) ( ) , 0 (3-18) 2 1 1 2 1 1 ( ) 1 1 2 2 1 2 2 2 2  − − − + − + − = −        − + −      − − − y t e e t t t   n   n       y(t) y(t) j s 平面 0  1 s2 s n j s 平面 0  1 s 2 s