
所以 lim sinx sin xo- x→xo 同理可证: lim cosx=cos xo x→x0 前顶 后页 返回
前页 后页 返回 lim sin sin . 0 0 x x x x 同理可证: lim cos cos . 0 0 x x x x 所以

例7证明:lim√1-x2=V1-x。2(x|<1). x→x0 证因为 i-e---l+ V1-x2+V1-x,3 ≤2x-y V1-x2 则6>0,取8=e1-x ,当0<|x-xl<6时, 2 IN-g2--x1s2x-<& V1-x好 这就证明了所需的结论. 前页 后页 返回
前页 后页 返回 例7 证明: lim 1 1 ( | | 1 ). 0 2 0 2 0 x x x x x 证 因为 2 2 0 0 0 2 2 0 | || | 1 1 1 1 x x x x x x x x 则 0, , 2 1 2 x0 取 0 当 时, 0 | | x x 2 2 0 0 2 0 2 | | | 1 1 | . 1 x x x x x 这就证明了所需的结论. 0 2 0 2 | | , 1 x x x

在上面例题中,需要注意以下几点: 1.对于6,我们强调其存在性.换句话说,对于固定 的ε,不同的方法会得出不同的6,不存在哪一个更 好的问题 2.6是不惟一的,一旦求出了δ,那么比它更小的正 数都可以充当这个角色. 3.正数ε是任意的,一旦给出,它就是确定的常数, 前顶 后页 返回
前页 后页 返回 在上面例题中, 需要注意以下几点: 1. 对于 , 我们强调其存在性. 换句话说, 对于固定 的 , 不同的方法会得出不同的 , 不存在哪一个更 好的问题. 数都可以充当这个角色. 3. 正数 是任意的,一旦给出,它就是确定的常数. 2. 是不惟一的, 一旦求出了 , 那么比它更小的正

有时为了方便,需要让ε小于某个正数.一旦对这 样的ε能找到相应的δ,那么比它大的ε,这个8 当然也能满足要求.所以我们有时戏称ε“以小 为贵”. 前页 后页 返回
前页 后页 返回 有时为了方便,需要让 小于某个正数. 一旦对这 为贵”. 当然也能满足要求. 所以我们有时戏称 “ 以小 样的 能找到相应的 , 那么比它大的 , 这个
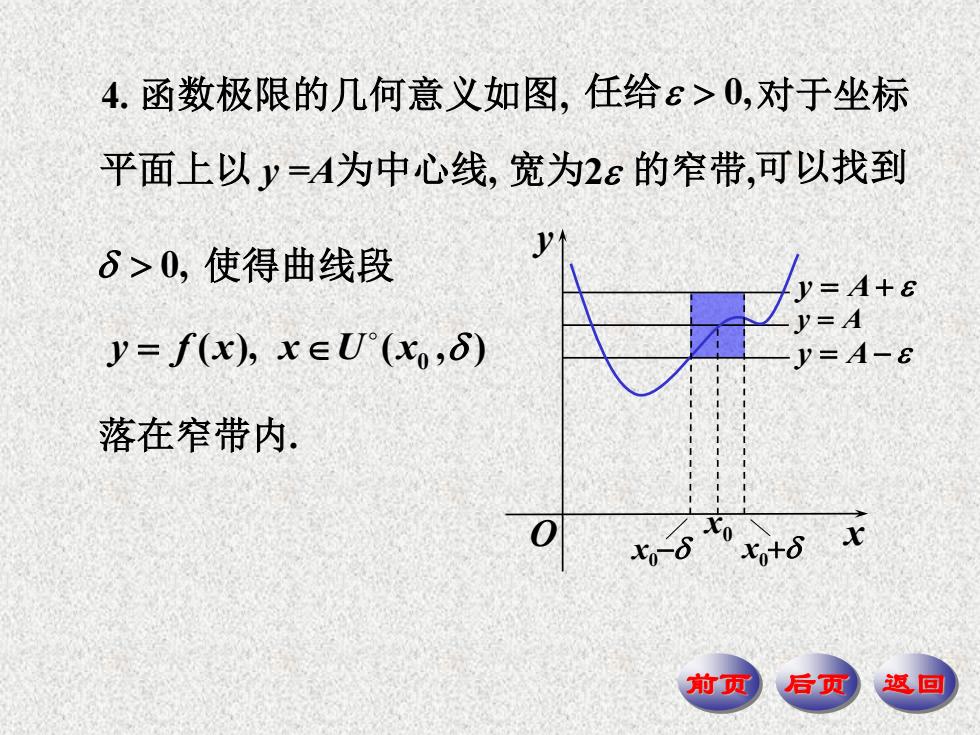
4.函数极限的几何意义如图,任给ε>0,对于坐标 平面上以y=A为中心线,宽为2ε的窄带,可以找到 δ>0,使得曲线段 y=A+a .=A y=f(x),x∈U(x,6) y=A-8 落在窄带内 x 前顶 后顶 返回
前页 后页 返回 平面上以 y =A为中心线, 宽为 2 的窄带, 可以找到 0, 使得曲线段 ( ), ( , ) y f x x U x0 4. 函数极限的几何意义如图, 任给 0, 对于坐标 落在窄带内. y A y A y A O x y x0 0 x x0