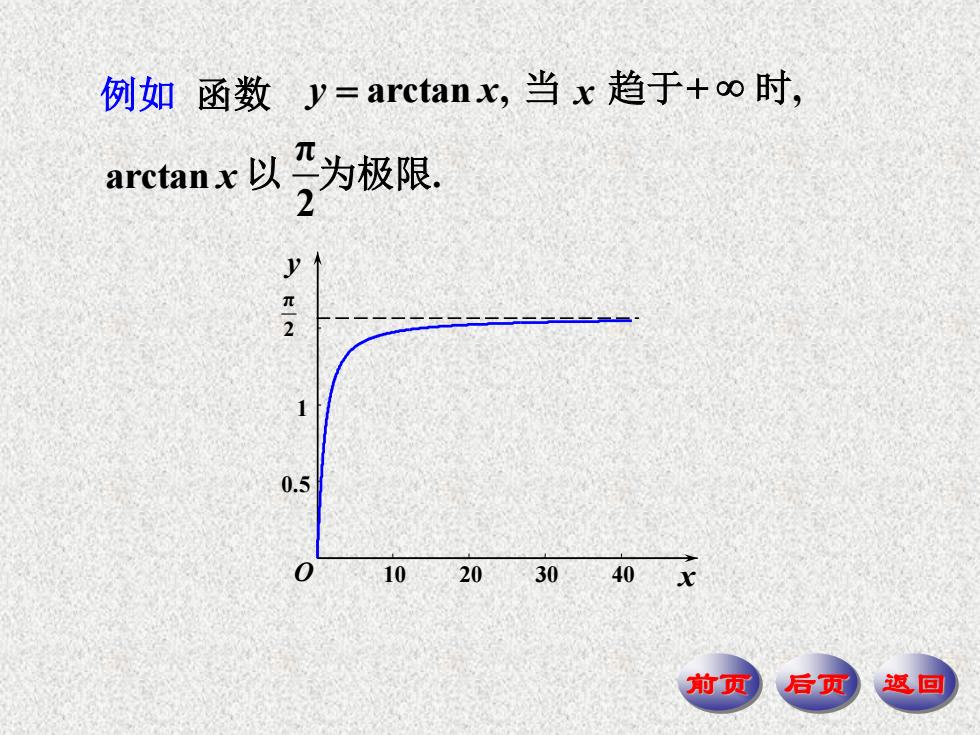
例如函数y=arctanx,当x趋于+oo时, arctanx以,为极限. 2 yT2 0.5 10 20 3040x 前顶 后页 返回
前页 后页 返回 例如 函数 y arctan x, 当 x 趋于 时, x y π 2 O 10 20 30 40 0.5 1 arctan x 以 为极限. π 2

定义1设f为定义在[a,+∞)上的一个函数.A为 定数,若对于任意正数s>0,存在M(≥),使得 当x>M时 f(x)-A<6, 则称函数f(x)当x趋于+∞时以A为极限, 记为 Iimf(x)=A或者f(x)→A(x-→+o). 前顶 后页 返回
前页 后页 返回 记为 lim ( ) 或者 x f x A f (x) A (x ). 定数, 若对于任意正数 0, 存在 M( a), 使得 f (x) A , 则称函数 f (x)当 x 趋于 时以 A为极限. 当x M 时, 定义1 设 f 为定义在a,上的一个函数. A 为
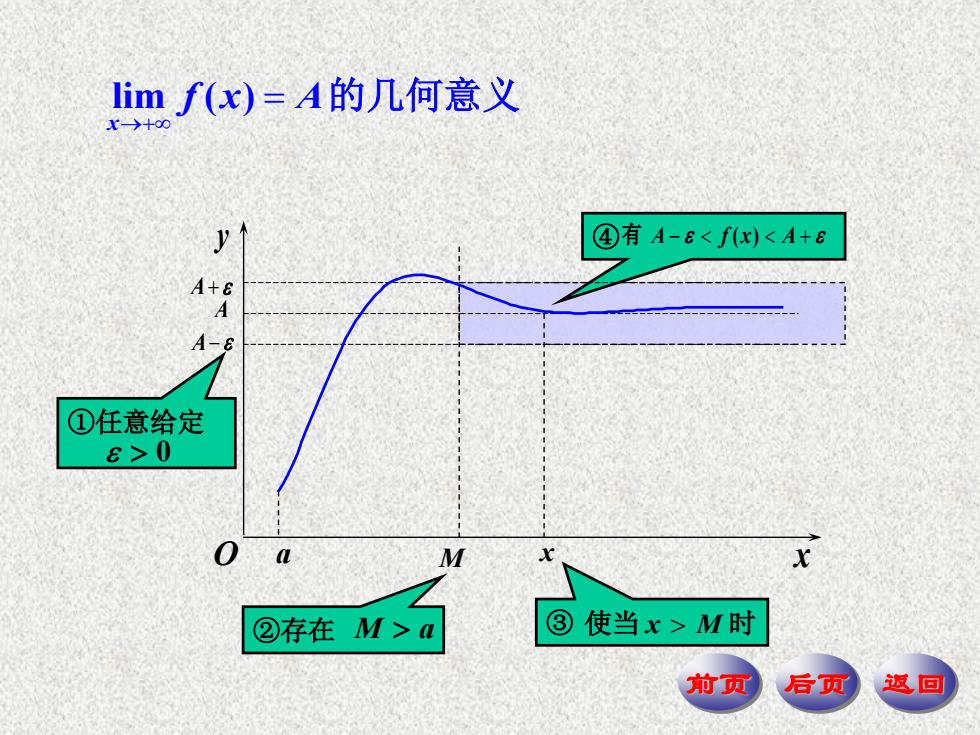
Iimf(x)=A的几何意义 →+00 y ④有A-6<f(x)<A+6 A+8 A A-8 ①任意给定 6>0 O a ②存在M>a ③使当x>M时 前页 后页 返回
前页 后页 返回 ④ 有 A f x A ( ) lim ( ) x f x A 的几何意义 ③ 使当 x M 时 x A A ①任意给定 0 M ②存在 M a A x y O a
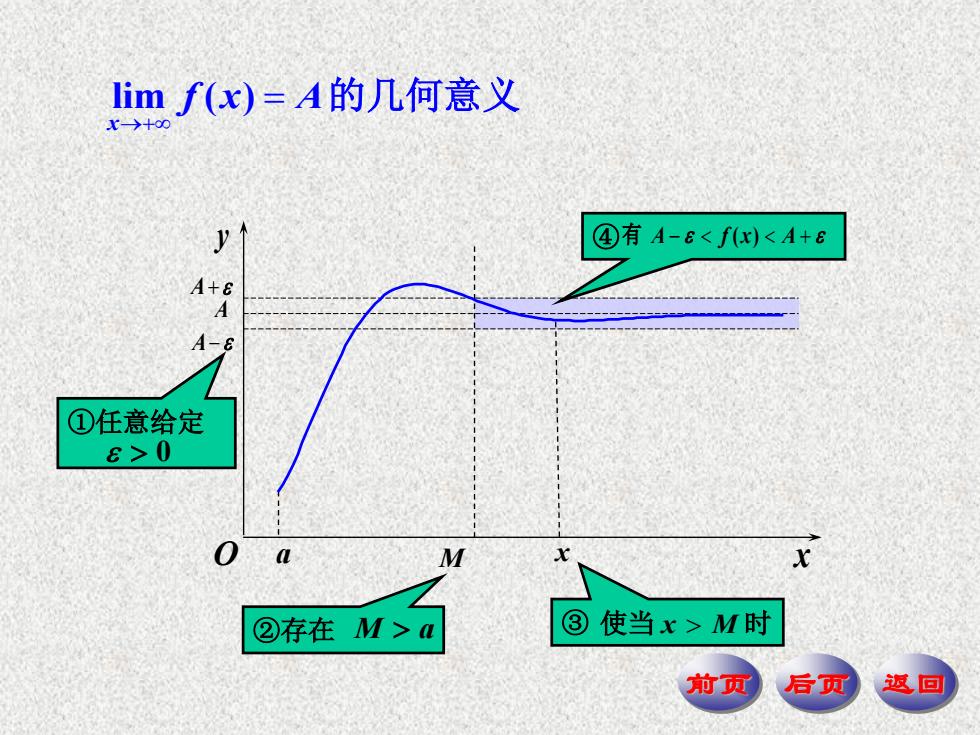
imf(x)=A的几何意义 +00 ④有A-G<fx)<A+6 A+6 A A-8 ①任意给定 6>0 0 X ②存在M>a ③使当x>M时 前页 后页 返回
前页 后页 返回 ④ 有 A f x A ( ) lim ( ) x f x A 的几何意义 ③ 使当 x M 时 x A A ①任意给定 0 M ②存在 M a x A y O a

注数列可视为定义在正整数集上的函数.请大家 比较数列极限定义与函数极限定义之间的相同点 与不同点 例1证明1im1=0. x→+o0X 证任给e>0,取M=1,当x>M时, 8 fx)-0= <8 所以(由定义1), lim=0. x→+0X 前顶 后页 返回
前页 后页 返回 注 数列可视为定义在正整数集上的函数. 请大家 所以(由定义1), 例1 证明 0. 1 lim x x 证 任给 0, 取 , 1 M 当 x M 时, , 1 ( ) 0 x f x 0. 1 lim x x 与不同点. 比较数列极限定义与函数极限定义之间的相同点