
航行问题建立数学模型的基本步骤 作出简化假设(船速、水速为常数,方向一致); 用符号表示有关量化,y表示船速和水速); ·用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程); 求解得到数学解答(x=20,y=5); 回答原问题(船速每小时20公里)
航行问题建立数学模型的基本步骤 • 作出简化假设(船速、水速为常数, 方向一致); • 用符号表示有关量(x, y表示船速和水速); • 用物理定律(匀速运动的距离等于速度乘以 时间)列出数学式子(二元一次方程); • 求解得到数学解答(x=20, y=5); • 回答原问题(船速每小时20公里)

录象机计数器的用途 经试验,一盘录像带从头走到尾, 时间用了183分30秒,计数器读数从 0000变到6152。在一次使用中录像带已 题 经转过大半,计数器读数为4580,问剩 下的一段还能否录下1小时的节目? 聚 不仅仅回答问题,而且建立计数器读数与 绿像带转过时间的关系 个数学模型 日常问题:常见的录音机的转轴转动是匀速的吗? 思考 本题中计数器读数是均匀增长的吗?
录象机计数器的用途 问 题 经试验,一盘录像带从头走到尾, 时间用了183分30秒,计数器读数从 0000变到6152。在一次使用中录像带已 经转过大半,计数器读数为4580,问剩 下的一段还能否录下1小时的节目? 要 求 不仅仅回答问题, 而且建立计数器读数与 录像带转过时间的关系——一个数学模型! 思考 本题中计数器读数是均匀增长的吗? 日常问题:常见的录音机的转轴转动是匀速的吗?

等 万 000 的 4
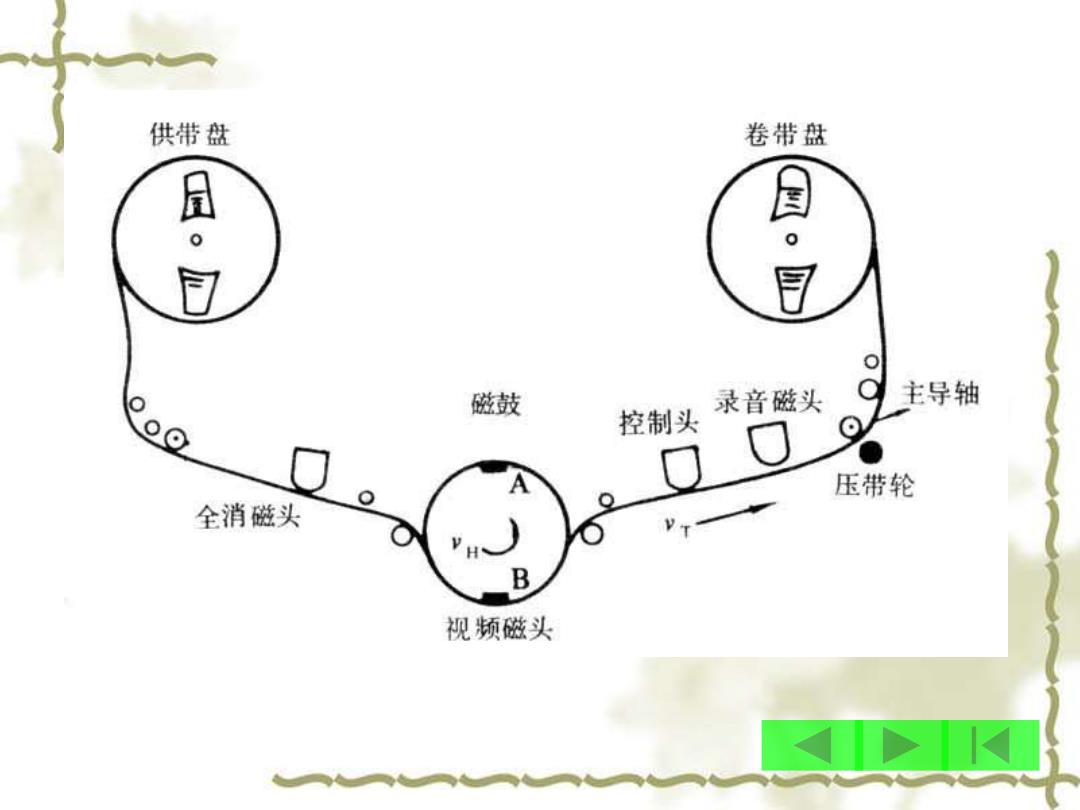
供带盘 卷带盘 员 0 0 包 磁鼓 录音磁头 主导轴 控制头 压带轮 全消磁头 B 视频磁头
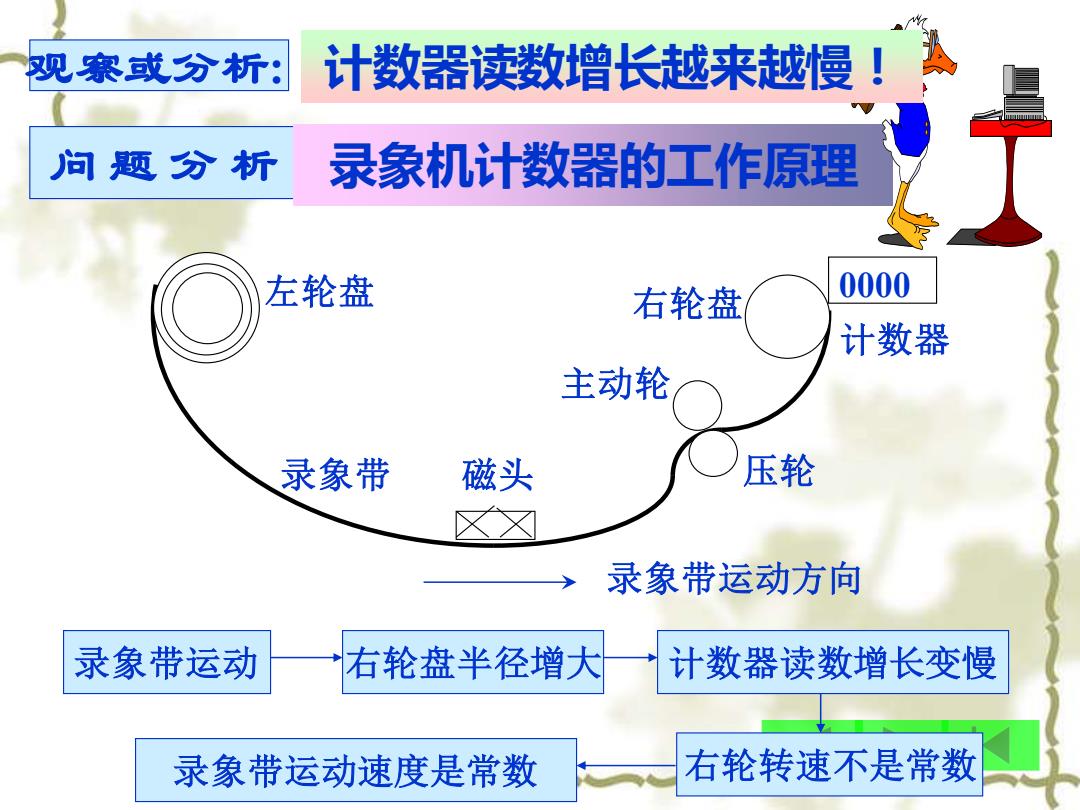
观察或分析: 计数器读数增长越来越慢! 问题分析 录象机计数器的工作原理 左轮盘 右轮盘 0000 计数器 主动轮 录象带 磁头 压轮 录象带运动方向 录象带运动 右轮盘半径增大 计数器读数增长变慢 录象带运动速度是常数 右轮转速不是常数
问 题 分 析 录象机计数器的工作原理 左轮盘 0000 右轮盘 磁头 主动轮 压轮 计数器 录象带 录象带运动方向 录象带运动 右轮盘半径增大 录象带运动速度是常数 右轮转速不是常数 计数器读数增长变慢 观察或分析: 计数器读数增长越来越慢!