
5-1月球的质量是地球的1/81,直径为地球的3/11,计算质量为65kg的 人在月球上所受的月球引力. 分析人在不同星球上所受引力均属万有引力,其大小由万有引力定律确 定,人在地球表面所受引力的大小,即人的重量.根据月球、地球的质量和半径, 采用比较引力的方法可得到人在月球表面所受的引力。 解设地球、月球的半径分别为R1、R2,它们的质量分别为m1、m2.根据 万有引力定律,人在地球表面所受的引力大小为 Ig -G 人在月球所受的引力大小为 F-GR 比较上述两式可得 F=m2R)2 miR2/mg 106 N

5-2试根据地球的半径RE和引力常量G的值,估算地球的质量和平均 密度.(已知Re=6.4×10m,G=6.7×10-11Nm2kg2) 分析利用地面上物体的重力也就是物体所受地球的万有引力,可解出地 球的质量,从而,由密度的定义可解此题、 解地面上物体的重力也就是物体所受地球的万有引力.故有 mg Gmem RE 4 mE=8是=6.0×1024kg 3 地球的密度为 mE=5.5×103kg·m-3 由于该平均密度大于地球表面的密度,由此可推断地球内部是由平均密度 较大的物质组戒

5-3如图5-3所示,有两个半径分别为R1和R2的同心薄壁球壳,质量 各为m1和m2.将质量为m的质点P置 于距球心O分别为rA、rg和rC处,求:(1) 质点P所受的引力;(2)如取质点在无限远 处的引力势能为零,计算质点P在以土三 处的引力势能. 分析(1)由教材中所得结论知:质量 均匀分布的球壳内任意质点受到球壳的引 图5-3 力为零:而球壳外任意质点所受球壳的引力,则可把球壳看作其质量集中于球心 处的质点来处理.根据上述结论和力的叠加原理即可得到质点在不同位置处的 引力.(2)根据均匀球壳内、外质点所受球壳的引力,由引力势能的定义可确定 质点在各处的势能值. 解(1)根据上述分析,在半径为R:的球壳内任意点A的引力为F1=0: 而点B处的质点受到的引力为F2=Gmm;点C处的质点受到球壳的引力为 r月 F=G(mitma)m r (2)根据引力势能的定义E。=F·d,当rc>R2时,有 Ec=F3·dr=-Gmmi+m2 re 当R1<rB<R2时,有 Eadrdr dr --Gm() r 同理,当ra<R1时,有 E-Gm(贤+》 可见,当质点处于球壳内部任意点时,它的势能都等于表面处的势能;而质点处 于球壳外部时,它的势能将随位置而改变
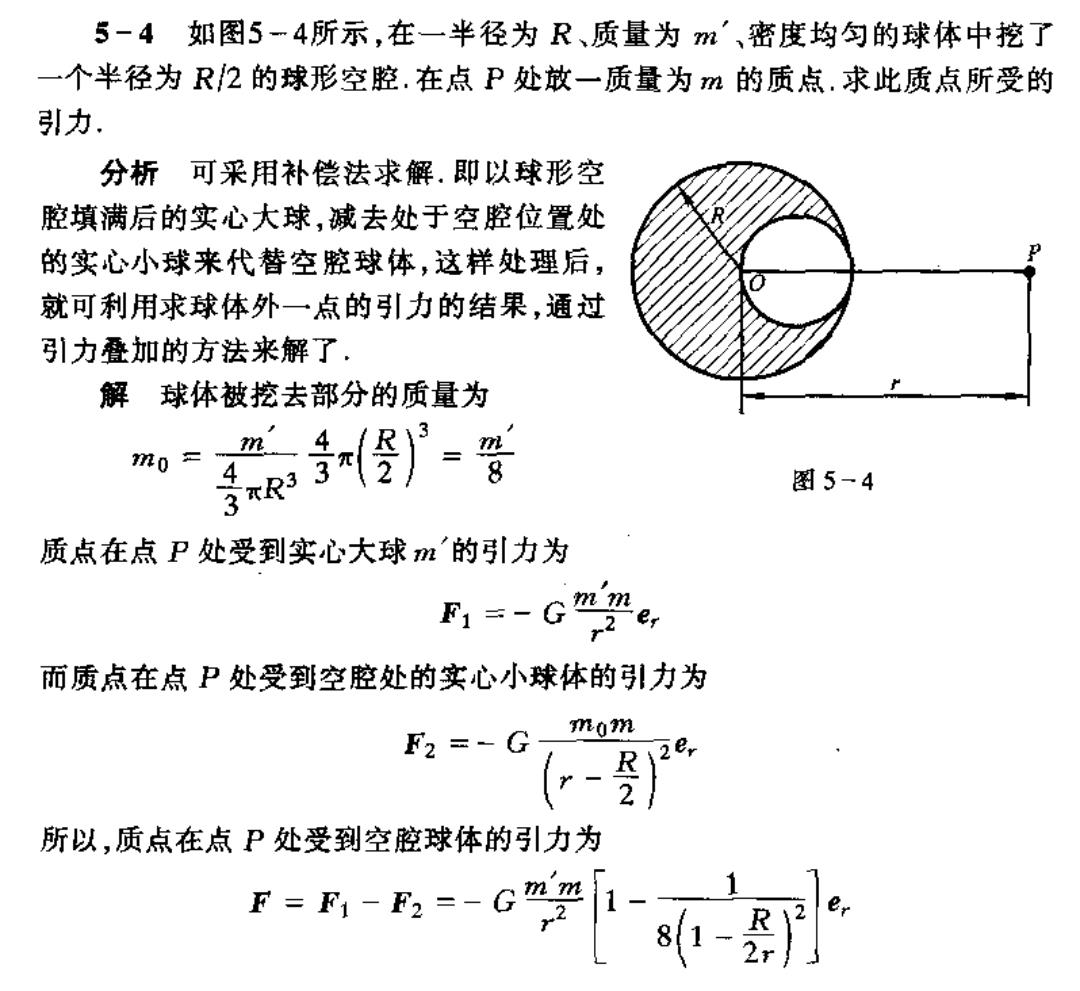
5-4如图5-4所示,在一半径为R、质量为m'、密度均匀的球体中挖了 一个半径为R2的球形空腔.在点P处放一质量为m的质点.求此质点所受的 引力. 分析可采用补偿法求解.即以球形空 腔填满后的实心大球,减去处于空腔位置处 的实心小球来代替空腔球体,这样处理后, 就可利用求球体外一点的引力的结果,通过 引力叠加的方法来解了, 解球体被挖去部分的质量为 m0= 答 质点在点P处受到实心大球m'的引力为 F1=-Ger 而质点在点P处受到空腔处的实心小球体的引力为 【2% F2=G mom 所以,质点在点P处受到空腔球体的引力为 F=F1-F2=-Gm[1- 1 2

5一5当一物体从地球表面竖直向上或向下移动一小距离时,计算重力加 速度的变化规律. 分析重力加速度即引力场强度,它可从引力场强度的定义求出.但是,必 须注意计算万有引力时,在题中两种情况下所用地球质量是不同的.当物体向地 心下移时,计算引力时的地球质量是指以地心至物体之间的距离为半径的球体 内的质量. 解设物体在地球表面上方的高度为h,则引力场强度的大小为 GmE gx=(R+h) 式中mE为地球的质量.考感到地球表面的重力加速度g= G,同时,h比R 小的多,可用二项式定理将分母展开,并略去小项,有 舒+)小-) gex=- GmE 取地球半径R=6.4×10m,重力加速度g=9.81ms2,代人上式得 gx=(9.81-3.06×10-6h)m·s2 如果物体向地球内部移动一距离,此时,在计算引力场强度时只需考虑半 径为r=R一h的地球内部的质量,因此,有 -GmE(&1 R3 gn=(9.81-1.53×106h)m·s2 从上述结果可看出,在地面上空和地下的引力场强度都要比地面的小,但是,向 地面上方移动时,引力场强度减少得快