
15-1频率为y=1.25×10z的平面简谐纵波沿细长的金属棒传播,棒 的弹性模量为E=1.90×101Nm-2,棒的密度p=7.6×103kgm-3.求该纵 波的波长 分析因机械波传播速度与介质性质有关,固体中纵波传播速度“三 √E可p.而波的特征量波长入与波速、频率y之间有A=u/.所以,频率一定的 振动在不同介质中传播时,其波长不同.由上述关系可求得波长 解由分析可知金属棒中传播的纵波速度“=√EP,因此,该纵波的波长 为 λ=ufy=VE/pw2=0.40m

15-2一横波在沿绳子传播时的波动方程为y=(0.20m)cs[(2.5πs1)t -(xm1)x].(1)求波的振幅、波速、频率及波长;(2)求绳上质点振动时的最大 速度;(3)分别画出t=1s和t=2s时的波形,并指出波峰和波谷.画出x 1.0m处质点的振动曲线并讨论其与波形图的不同. 分析(1)已知波动方程(又称波函数)求波动的特征量(波速u、频率、振 幅A及波长入等),通常采用比较法.将已知的波动方程按波动方程的一般形式 y=As[(t干)+9o]书写,然后通过比较确定各特征量(式中孟前“-”、 “+”的选取分别对应波沿x轴正向和负向传播).比较法思路清晰、求解简便, 是一种常用的解题方法.(2)讨论波动问题,要理解振动物理量与波动物理量之 间的内在联系与区别.例如区分质点的振动速度与波速的不同,振动速度是质点 的运动速度,即v=dy/dt;而波速是波线上质点运动状态的传播速度(也称相位 的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定.介 质不变,波速保持恒定.(3)将不同时刻的:值代人已知波动方程,便可以得到不 同时刻的波形方程y=y(x),从而作出波形图.而将确定的x值代入波动方程 便可以得到该位置处质点的运动方程y=y(t),从而作出振动图 解(1)将已知波动方程表示为 v=(0.20m)cos「(2.5πs1)(t~xf2.5m·s1)1 与一般表达式y=Acos[ω(t-x/u)+p0]比较,可得 A=0.20m,u=2.5m·s1,p8=0 则 y=w/2π兰1.25Hz,λ=u/y=2.0m (2)绳上质点的振动速度 v=dy/dt=-(0.5rm·s1)sin[(2.5πsi)(t-x2.5m·s1)] 则 Umax=1.57 m's-1 (3)t=1s和t=2s时的波形方程分别为 y1=(0.20m)co8[2.5π-(rm1)x】 y2=(0.20m)cos[5π-(πm1)x] 波形图如图15-2(a)所示. x=1.0m处质点的运动方程为 y=*(0.20m)cos(2.5xs1)t 振动图线如图15-2(6)所示. 被形图与振动图虽在图形上相似,但却有着本质的区别.前者表示某确定时 刻波线上所有质点的位移情况,而后者则表示某确定位置的一个质点,其位移随 时间变化的情况, b 图15-2

15-3波源作简谐运动,其运动方程为y=(4.0×10-3m)cs(240πs1)t, 它所形成的波形以30m·s1的速度沿一直线传播.(1)求波的周期及波长;(2) 写出波动方程. 分析已知波源运动方程求波动物理量及波动方程,可先将运动方程与其 一般形式y=Acos(t+p)进行比较,求出振幅A、角频率w及初相P0,而这三 个物理量与波动方程的一般形式y=Acos[w(t一x/w)+p0]中相应的三个物 理量是相同的.再利用题中已知的波速4及公式仙=2ry=2x/T和入=uT即可 求解. 解(1)由已知的运动方程可知,质点振动的角频率w=240πs1.根据分 析中所述,波的周期就是振动的周期,故有 T=2w=8.33×10-38 波长为 入=uT=0.25m (2)将已知的波源运动方程与简谐运动方程的一般形式比较后可得 A=4.0×10-3m,w=240ms1,p0=0 故以波源为原点,沿x轴正向传播的波的波动方程为 y =Acos[w(t-xlu)+9o] =(4.0×10-3m)cos[(240πs1)t-(8rm1)x]
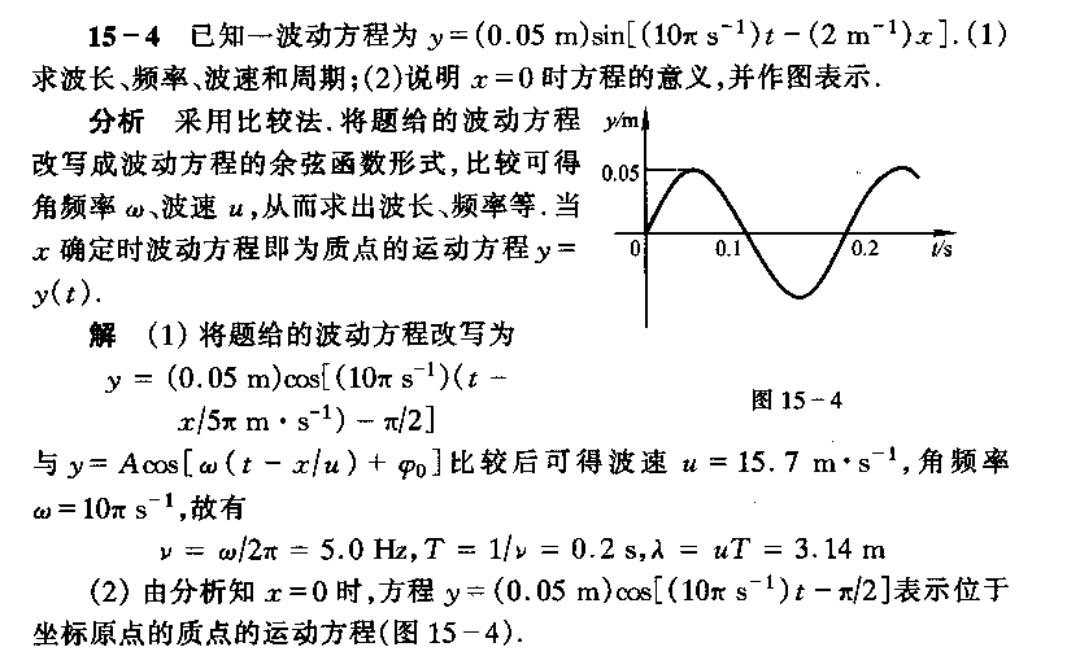
15-4已知-一波动方程为y=(0.05m)sin[(10xs1)t-(2m1)x].(1) 求波长、频率、波速和周期;(2)说明x=0时方程的意义,并作图表示. 分析采用比较法.将题给的波动方程血 改写成波动方程的余弦函数形式,比较可得0.5 角频率仙、波速,从而求出波长、频率等.当 x确定时波动方程即为质点的运动方程y= 0.2於 y(t). 解(1)将题给的波动方程改写为 y=(0.05m)os[(10πs1)(t- 图15“4 x/5πm·s1)-π/2] 与y=Acos[ω(t-x/u)+p0】比较后可得波速w=15.7m·s1,角频率 ω=10πs1,故有 y=w/2x=5.0Hz,T=1/y=0.2s,入=T=3.14m (2)由分析知x=0时,方程y÷(0.05m)cos[(10rs1)t-π2]表示位于 坐标原点的质点的运动方程(图15-4)

15-5波源作简谐运动,周期为0.02s,若该振动以100m·s1的速度沿直 线传播,设t=0时,波源处的质点经平衡位置向正方向运动,求:(1)距波源 15.0m和5.0m两处质点的运动方程和初相:(2)距波源为16.0m和17.0m 的两质点间的相位差. 分析(1)根据题意先设法写出波动方程,然后代入确定点处的坐标,即得 到质点的运动方程.并可求得振动的初相.(2)波的传播也可以看成是相位的传 播.由波长入的物理含意,可知波线上任两点间的相位差为△p=2π△x/入. 解(1)由题给条件T=0.02s,u=100ms1,可得 w=2mT=100πs1;入=uT=2m 当t=0时,波源质点经平衡位置向正方向运动,因而由旋转矢量法可得该 质点的初相为0=-π2(或3π2).若以波源为坐标原点,则波动方程为 y=Acos[(100xs1)(t-x/100m·s1)-π2] 距波源为x1=15.0m和x2=5.0m处质点的运动方程分别为 y1=Acos[(100rs1)t-15.5x] y2=Acos[(100πs1)t-5.5π] 它们的初相分别为p0=-15.5π和P20=一5.5π(若波源初相取Po=3π2,则 初相p10=-13.5π,p20=-3.5元.) (2)距波源16.0m和17.0m两点间的相位差 △9=P1-P2=2π(x2-x1)/1=π