第十五章波动光学 题1511在双键干浅实验中,两辩距为0.30mm,用单色光兵直照双斜,在离缝120m 的饼上测得中央明饺一侧第5条暗议与另一侧第5条暗议间的混高为2278mm.问所用光的 波长为多少,是什么佩色的光: 题151分析:在双缝干游中,屏上喻纹隐型由x=号2以+)子决定,所谓第5条暗牧是指 对应春-4的惠一级暗纹。由于条救对称,该验纹到中爽明纹中心的距x= 2 m,那么 由暗纹公式即可求得波长1。 此外,因秋缝干涉是等间距的,故也可用条纹间距公式一:无成入射完被K、匝注意 d 丙个第5条暗级之可所色含的相邻条纹间隔数为9(不是10,为什么?。放红-2眉 9 解:解上暗数的位置=k+学把4,=马 m以及d,d'值代入,可得 2 入-6238m,为红光. 解2:所上相统暗议(坟明议)何先r-号,把r-2飞m 巴m,以及d,d值代人,可 d 9 得1=6238nm. 思152:在劳埃德镜实险中,将拼P紫靠平内镜M右边缘L点放置,如图所,已知单色光 薄s的波长无=20m,求十血镜白边缘L到所上元一条明敛问的距高。 题152分析:劳埃仙悦实验中的反1光可看成山返尤夏S所发出,尤系S与S是州十光漯, 在所P上,由它们形猛的下涉结果与绿d一40四m,篷与屏的间距d-0cm的双算千楼相 似。不月之处在于劳埃德鲶中的反射光,山于存在相位:的突变而有半波损失,故屏上明暗 纹位置正好互挨,人.处纹而不是切文、 2.0mm -----757777Z77 S. 20m 3Ucm
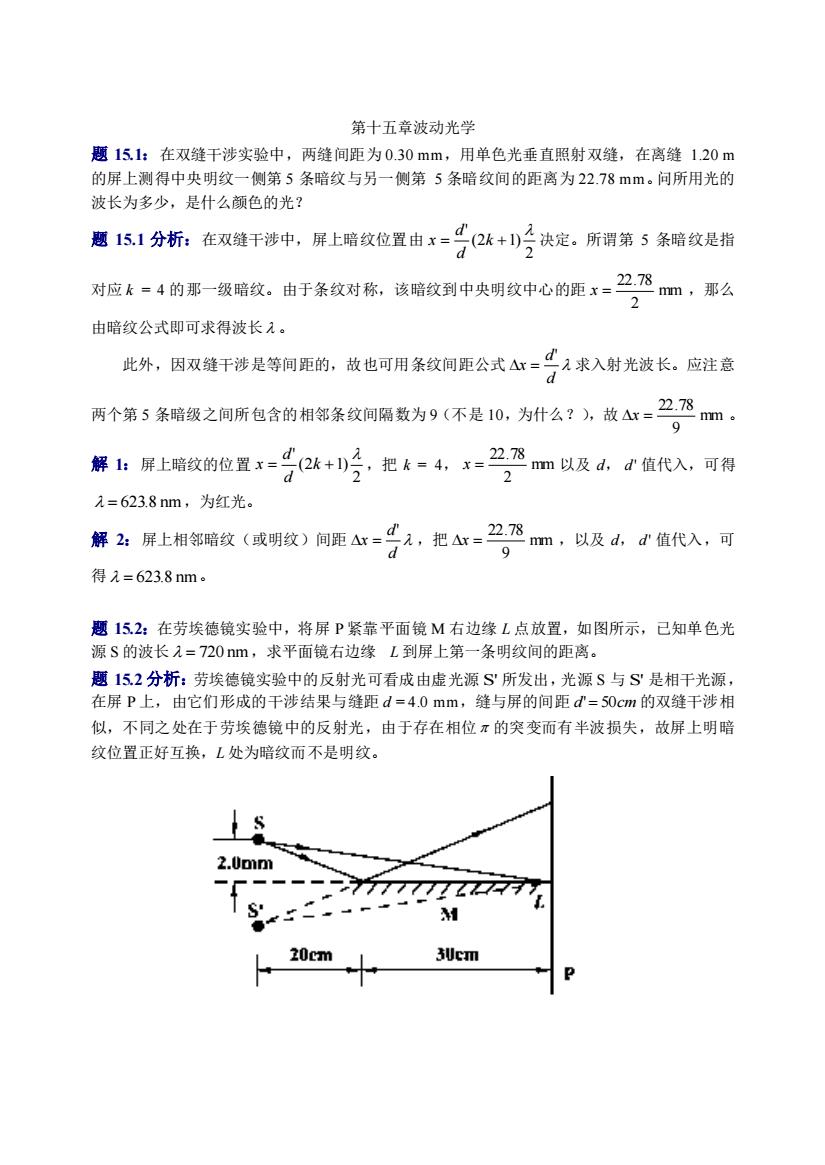
第十五章波动光学 题 15.1:在双缝干涉实验中,两缝间距为 0.30 mm,用单色光垂直照射双缝,在离缝 1.20 m 的屏上测得中央明纹一侧第 5 条暗纹与另一侧第 5 条暗纹间的距离为 22.78 mm。问所用光的 波长为多少,是什么颜色的光? 题 15.1 分析:在双缝干涉中,屏上暗纹位置由 2 (2 1) ' = k + d d x 决定。所谓第 5 条暗纹是指 对应 k = 4 的那一级暗纹。由于条纹对称,该暗纹到中央明纹中心的距 mm 2 22.78 x = ,那么 由暗纹公式即可求得波长 。 此外,因双缝干涉是等间距的,故也可用条纹间距公式 d d x ' = 求入射光波长。应注意 两个第 5 条暗级之间所包含的相邻条纹间隔数为 9(不是 10,为什么?),故 mm 9 22.78 x = 。 解 1:屏上暗纹的位置 2 (2 1) ' = k + d d x ,把 k = 4, mm 2 22.78 x = 以及 d, d ' 值代入,可得 = 623.8 nm ,为红光。 解 2:屏上相邻暗纹(或明纹)间距 d d x ' = ,把 mm 9 22.78 x = ,以及 d, d ' 值代入,可 得 = 623.8 nm。 题 15.2:在劳埃德镜实验中,将屏 P 紧靠平面镜 M 右边缘 L 点放置,如图所示,已知单色光 源 S 的波长 = 720 nm ,求平面镜右边缘 L 到屏上第一条明纹间的距离。 题 15.2 分析:劳埃德镜实验中的反射光可看成由虚光源 S' 所发出,光源 S 与 S' 是相干光源, 在屏 P 上,由它们形成的干涉结果与缝距 d = 4.0 mm,缝与屏的间距 d' = 50cm 的双缝干涉相 似,不同之处在于劳埃德镜中的反射光,由于存在相位 的突变而有半波损失,故屏上明暗 纹位置正好互换,L 处为暗纹而不是明纹

解:设x为双缝干沙中相架明纹(或暗纹)之间的间距,L到屏上第一条明纹间距离为 Ax=Ar=1A 22d 把d,d”以及2的值代入,可得x=4.5×10m, 思153如图所示。出光源S发出的元-600m的单色光,白室气射入折射率m-123的一 层进明物质,再射入空气。若透明物质的厚度为d-10cm,入射角8=30,且S4-C-5.0 m,求:(1)折射角A,为多少?(2)此单色光在这层透明物质里的规率、速度和液长各为 多少?(3)S到C的几何路程为多少?光程又为多少? 空气 n" 空气 I B 愿15,3解!>由折射定律m2 =n可得 sine 712324 (2》单色光在透明介质中的速度?。·被长入和類率分别为 ,-£-24×10°mg 不-2-48×10-7m-488m v-号=50x104B (3》S到C的几何路程为
解:设 x 为双缝干涉中相邻明纹(或暗纹)之间的间距,L 到屏上第一条明纹间距离为 d x d x ' 2 1 2 = = 把 d, d ' 以及 的值代入,可得 x = 4.5×10-5 m。 题 15.3:如图所示。由光源 S 发出的 = 600 nm 的单色光,自空气射入折射率 n = 1.23 的一 层透明物质,再射入空气。若透明物质的厚度为 d = 1.0 cm,入射角 = 30 ,且 SA = BC = 5.0 cm,求:(1)折射角 1 为多少?(2)此单色光在这层透明物质里的频率、速度和波长各为 多少?(3)S 到 C 的几何路程为多少?光程又为多少? 题 15.3 解:(1)由折射定律 = n 1 sin sin 可得 24 1.23 sin 30 arcsin sin arcsin 0 1 = = = n (2)单色光在透明介质中的速度 n v ,波长 n 和频率 分别为 8 1 2.44 10 m s − = = n c vn 4.88 10 m 488 nm 7 = = = − n n 5.0 10 Hz 14 = = c (3)S 到 C 的几何路程为

SC=S4+AB+BC -S4+-d +BC=0111m se S到C的光程为 ∑n,D=Sx1+A×n+BCx1-0114m 愿154:在折射辛n,=152的服相机镜头表面涂有一层折射率,=13驾的Mg增透膜,若 比装仅适用于波长克=550m的光,此膜的最小厚度为多少? 题154分析:在神模干沙中,携的材料及厚度都将对两反射光〔或两透射光)的光程差产生 影响,从而可使某些波长的光在反射(或透射)中得到加强或减函,这种选择性使薄瓶干沙 在工程技术上有很多应用。本避所述的消济膜,就是希择波长2=550m的光在消射中得到 加强,从而得到所希显的照相效果(因感光底片对此被长附近的光最为傲感),具体求解时应 注意在d>0的前提下,k取最小的允许值, 解1:因干涉的互补性,波长为S50m的光在透射中得到加强,则在反射中一定减病,两反 射光的光程差4,-2nd,由下涉相消条件4,=+)宁,3 d-2+) 4与 取k-0,则d.。=99.3hm 解2:由于空气的折射竿肌=,且有州<肚<形,则对透射光而言,两相干光的光程差 4=2m,d+2 ,出干渗加强条件4=材,得 d=-22m 、元 数k=1,划模的最小厚度d。=9.3m 思155:利用空气跨尖测细丝直径。如图所示,已知A-5893nm,L=2.888×102m,测得 30条条蚊的总宽度为4295×103m,求细丝直径d
SC = SA+AB+BC = SA+ 1 cos d + BC = 0.111 m S 到 C 的光程为 niDi = SA1+ ABn+ BC1= 0.114m 题 15.4:在折射率 n3 = 1.52 的照相机镜头表面涂有一层折射率 n2 = 1.38 的 MgF2 增透膜,若 此膜仅适用于波长 = 550 nm 的光,则此膜的最小厚度为多少? 题 15.4 分析:在薄膜干涉中,膜的材料及厚度都将对两反射光(或两透射光)的光程差产生 影响,从而可使某些波长的光在反射(或透射)中得到加强或减弱,这种选择性使薄膜干涉 在工程技术上有很多应用。本题所述的增透膜,就是希望波长 = 550 nm 的光在透射中得到 加强,从而得到所希望的照相效果(因感光底片对此波长附近的光最为敏感)。具体求解时应 注意在 d>0 的前提下,k 取最小的允许值。 解 1:因干涉的互补性,波长为 550nm 的光在透射中得到加强,则在反射中一定减弱,两反 射光的光程差 2 = 2n2d ,由干涉相消条件 2 (2 1) 2 = k + ,得 4 2 (2 1) n d k = + 取 k = 0,则 dmin = 99.3 nm 解 2:由于空气的折射率 nl = 1,且有 n1<n2<n3,则对透射光而言,两相干光的光程差 2 1 2 2 = n d + ,由干涉加强条件 1 = k ,得 2 2 ) 2 ( n d k = − 取 k = l,则膜的最小厚度 dmin = 99.3 nm 题 15.5:利用空气劈尖测细丝直径。如图所示,已知 = 589.3 nm ,L = 2.888×10-2 m,测得 30 条条纹的总宽度为 4.295×10-3 m,求细丝直径 d

思155分析:在应用跨尖干涉公式d=入L时,应注意相g条纹的间距方是N条条纹的定 2n5 度△x除以(N-I)。 解:由分析知,相邻条纹间距6=红 ,则细丝直径为 N-1 d-LN-DL=5. 2n,b2n△x 题156:在利用牛顿环测未知单色光被长的实验中,当用已知波长为5893nm的钠黄光垂丝 照射时,测得第一和第四暗环的距离为△山=400×0-3m:当用波长未知的单色光来直照射 时,测得第一和第四暗环的距离为=3.85x10-3m,求该单色光的波长. 题156分析:牛领环装置产生的干涉暗环半径r=√阳,其中k-0,1,2…,k-0,对应 牛顿环中心的暗斑,素一1和真一4则对应第一和第四暗环,由它们之间的间距 山=乃一片=及,可知少xV反,需此可按圈中的测量方法求出未知彼长, 解:根据分析有 “-风 故未知光被长~546nm. 画1571用波长为589.3m的钠黄光见察牛顿环,测得某一明环的半径为1.0×103m,而 其外第四个明环的半轻为3.0×10」m,求平凸请镜凸面的曲率华径。 思157解:设题中所述两个明环分别对应级和(十4》领明纹。则有 解上述两式可 R--339m 4 恩15%:牛顿环装置中,透镜的曲率华径R-40m,用单色光垂直照射,在反射光中观旅某 一援暗环的半径r-2.5mm。现把平板玻璃向下平移d。=5.0um,上述被观黎暗环的半径变 为何值? 思158分析:在平板向下平移后,牛顿环中空气膜的厚度整体增厚。由等厚干涉原理可知
题 15.5 分析:在应用劈尖干涉公式 L nb d 2 = 时,应注意相邻条纹的间距 b 是 N 条条纹的宽 度 x 除以(N-1)。 解:由分析知,相邻条纹间距 −1 = N x b ,则细丝直径为 5.75 10 m 2 ( 1) 2 5 2 2 − = − = = L n x N L n b d 题 15.6:在利用牛顿环测未知单色光波长的实验中,当用已知波长为 589.3 nm 的钠黄光垂直 照射时,测得第一和第四暗环的距离为 4.00 10 m −3 r = ;当用波长未知的单色光垂直照射 时,测得第一和第四暗环的距离为 ' 3.85 10 m −3 r = ,求该单色光的波长。 题 15.6 分析:牛顿环装置产生的干涉暗环半径 r = kR ,其中 k = 0,1,2…,k = 0,对应 牛顿环中心的暗 斑,k = 1 和 k = 4 则对应第一和第 四暗环,由 它们之间的 间距 r = r4 − r1 = R ,可知 r ,据此可按题中的测量方法求出未知彼长 ' 。 解:根据分析有 ' ' = r r 故未知光波长 ' = 546 nm。 题 15.7:用波长为 589.3 nm 的钠黄光观察牛顿环,测得某一明环的半径为 1.0×10-3 m,而 其外第四个明环的半径为 3.0×10-3 m,求平凸透镜凸面的曲率半径。 题 15.7 解:设题中所述两个明环分别对应 k 级和(k+4)级明纹,则有 ) , 2 1 ( rk = k − R r k ]R 2 1 [( 4) k+4 = + − 解上述两式可得 3.39 m 4 2 k 2 k 4 r r R − = + 题 15.8:牛顿环装置中,透镜的曲率半径 R = 40 cm,用单色光垂直照射,在反射光中观察某 一级暗环的半径 r = 2.5 mm。现把平板玻璃向下平移 d0 = 5.0 m ,上述被观察暗环的半径变 为何值? 题 15.8 分析:在平板向下平移后,牛顿环中空气膜的厚度整体增厚。由等厚干涉原理可知
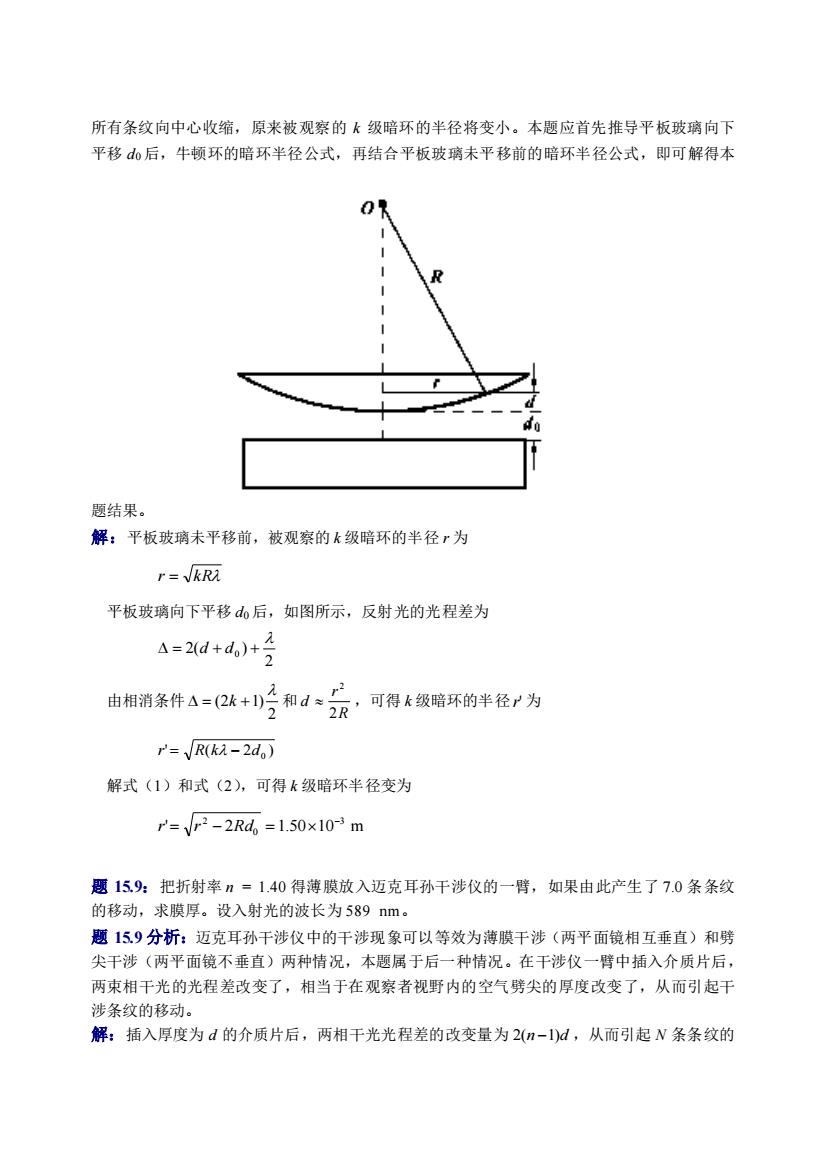
所有条纹向中心收缩,原来被观察的k级帝环的半径将变小。本题应首先推导平板玻璃向下 平移山后,牛环的暗环半径公式,再结合平板玻璃未平移前的暗环半径公式,即可解得本 愿结果。 解:平板玻璃未平移前,被观察的k级暗环的半径r为 r=kR就 平板玻璃向下平移山后,如医所示,反射光的光程差为 4-2d+d》+ 由相清条件4=2+2和d= 2 产2R·可得质缓暗环的半径了为 =yR(k-2d,) 解式(1)和式(2),可得k级暗环半径变为 r=VP2-2R4=1.50×10m 恶15:把折射率n-1.40得薄膜放入迈克耳孙干涉仪的其,如果由此产生了7.0条条纹 的移动,求膜厚。设入射光的被长为589nm。 题159分析:迈克耳豫干涉仅中的干涉现象可以等效为薄锁干涉(两平面镜相互垂直)和剪 尖干涉(两平面镜不垂直)两种情况,本题属于后一种情况。在干涉仪一臂中插入介顺片后, 两束相干光的光程养改变了,相当于在观察者视野内的空气劈尖的厚度改变了,从而引起干 涉条纹的移动。 解:插入厚度为d的介质片后,两相干光光程差的改变量为2(m-1d,从而引起N条条纹的
所有条纹向中心收缩,原来被观察的 k 级暗环的半径将变小。本题应首先推导平板玻璃向下 平移 d0 后,牛顿环的暗环半径公式,再结合平板玻璃未平移前的暗环半径公式,即可解得本 题结果。 解:平板玻璃未平移前,被观察的 k 级暗环的半径 r 为 r = kR 平板玻璃向下平移 d0 后,如图所示,反射光的光程差为 2 2( ) 0 = d + d + 由相消条件 2 (2 1) = k + 和 R r d 2 2 ,可得 k 级暗环的半径 r' 为 ' ( 2 ) d0 r = R k − 解式(1)和式(2),可得 k 级暗环半径变为 ' 2 1.50 10 m 3 0 2 − r = r − Rd = 题 15.9:把折射率 n = 1.40 得薄膜放入迈克耳孙干涉仪的一臂,如果由此产生了 7.0 条条纹 的移动,求膜厚。设入射光的波长为 589 nm。 题 15.9 分析:迈克耳孙干涉仪中的干涉现象可以等效为薄膜干涉(两平面镜相互垂直)和劈 尖干涉(两平面镜不垂直)两种情况,本题属于后一种情况。在干涉仪一臂中插入介质片后, 两束相干光的光程差改变了,相当于在观察者视野内的空气劈尖的厚度改变了,从而引起干 涉条纹的移动。 解:插入厚度为 d 的介质片后,两相干光光程差的改变量为 2(n −1)d ,从而引起 N 条条纹的