
5-6有一质量为m的质点,从地面上空高为五处落下,设空气阻力不 计,且h与地球半径RE相比要小得多.试证质点落地时的速率为 √/2 ghRef(RE+h). 分析质点下落是由于地球引力的作用.如将质点和地球视为系统,因系统 无外力作功,而仅有的引力又是保守内力(有心力),所以,系统的机械能(包括万 有引力势能和动能)守恒,根据机械能守恒定律,由引力势能的一殷表达式 -Gmemlr及质点在地面时的重力加速度g=Gme/R邑,可得质点落地时的动 能,并可求出质点落地时的速率, 证根据系统的机械能守恒定律有 mme -GRE+九 -G+2m2 而重力加速度 g= GmE R 由上述两式可得 2ghRe ”=N(RE+h)

5一7同步卫星在赤道上空以和地球自转同样的角速度运行,为满足这一 要求,同步卫星应位于距赤道多高的地方?其线速度为多大? 分析(1)地球自转的角速度可由一昼夜的时间来确定.当同步卫星以此 角速度作圆周运动时卫星和地球同步,所需的向心力正好是由地球对卫星的万 有引力来提供的.此时的万有引力可用于决定卫星的高度.(2)由角量与线量的 关系,可得到卫星的线速度, 2 解地球自转的角速度为0E=24×号600s1.同步卫星以此角速度作圆周 运动时,有 mmE C(RE+h产=mw(RE+h) 式中引力常量G、地球的质量mE和半径Rε可查表知.则同步卫星距赤道的高 度为 h=Gmg 1/3 -RE=3.59×107m 同步卫星的线速度为 v=wE(RE+h)=3.07×103m·sl
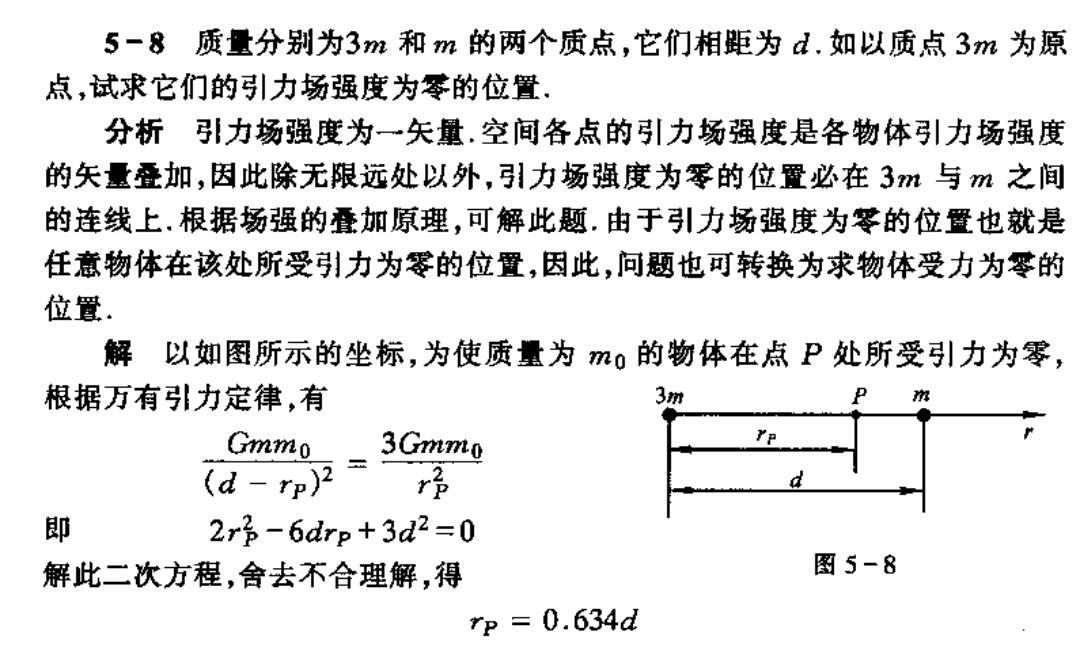
5-8质量分别为3和m的两个质点,它们相距为d.如以质点3m为原 点,试求它们的引力场强度为零的位置. 分析引力场强度为一矢量.空间各点的引力场强度是各物体引力场强度 的矢量叠加,因此除无限远处以外,引力场强度为零的位置必在3与m之间 的连线上.根据场强的叠加原理,可解此题.由于引力场强度为零的位暨也就是 任意物体在该处所受引力为零的位置,因此,问题也可转换为求物体受力为零的 位置. 解以如图所示的坐标,为使质量为m0的物体在点P处所受引力为零, 根据万有引力定律,有 3 Gmmo 3Gmmo (d-p2= r吊 即 2r3-6drp+3d2=0 解此二次方程,舍去不合理解,得 图5-8 rp=0.634d