
14-1有一个弹簧振子,振幅A=2.0×10-2m,周期T=1.0s,初相p= 3元4.试写出它的运动方程,并作出x-t图、℃-t图和a-t图. 分析弹簧振子的振动是简谐运动.振幅A、初相p、角频率ω是简谐运动 方程x=Acos(t+P)的三个特征量.求运动方程就要设法确定这三个物理量 题中除A、9已知外,仙可通过关系式w=2T确定,振子运动的速度和加速度 的计算仍与质点运动学中的计算方法相同, 解因仙=2xT,则运动方程 x=Acos(at+p)=A0s2+p】 根据题中给出的数据得 x=(2.0×10-2m)cos[(2πs1)t+0.75x] 振子的速度和加速度分别为 o=dx/dt=-(4x×10-2m·sl)sin[(2xs)t+0.75元] a=dx/dt2=-(82×10-2m·sl)cos[(2xs1)t+0.75x] x-t、v-t及a-t图如图14-1所示
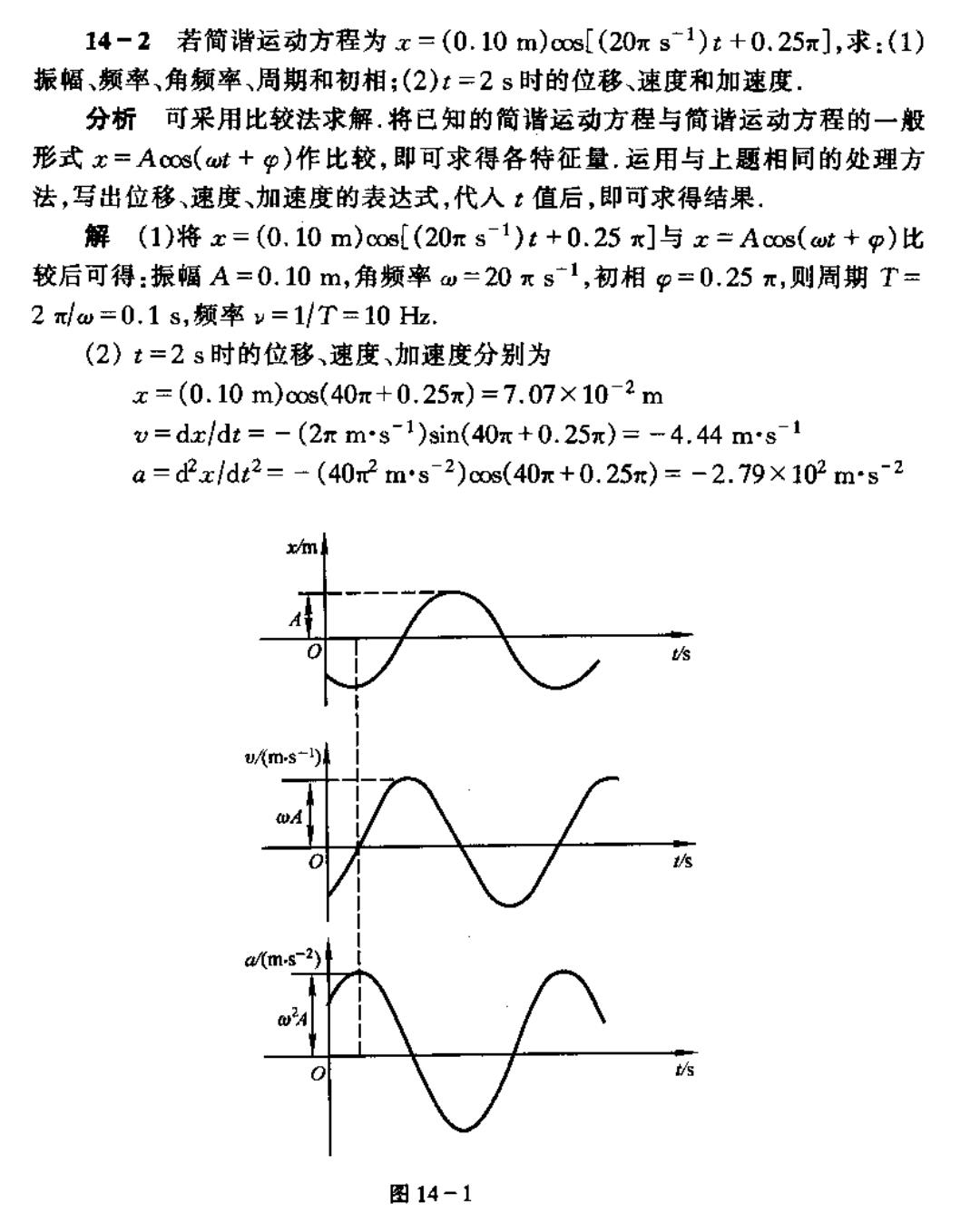
14-2若简谐运动方程为x=(0.10m)c0s[(20πs1)t+0.25π],求:(1) 振幅、频率、角颜率、周期和初相:(2)t=2s时的位移、速度和加速度. 分析可采用比较法求解.将已知的简谐运动方程与简谐运动方程的一般 形式x=Acos(at+p)作比较,即可求得各特征量.运用与上题相同的处理方 法,写出位移、速度、加速度的表达式,代人t值后,即可求得结果。 解(1)将x=(0.10m)cos[(20rs1)t+0.25x]与x=Acos(t+p)比 较后可得:振幅A=0.10m,角频率w=20元s1,初相9=0.25元,则周期T= 2πw=0.1s,缬率=1/T=10Hz. (2)t=2s时的位移、速度、加速度分别为 x=(0.10m)cos(40π+0.25π)=7.07×10-2m =dx/dt=-(2rms1)sin(40x+0.25π)=-4.44ms1 a=d2x/dt2=-(402ms2)cos(40π+0.25π))=-2.79×102m's2 /m 图14-1

14-3 一远洋货轮,质量为m,浮在水面时其水平截面积为S.设在水面 附近货轮的水平截面积近似相等,水的密度为P,且不计水的粘滞阻力,证明货 轮在水中作振幅较小的竖直自由运动是简谐运动,并求振动周期. {a) 图14-3 分析要证明货轮作简谐运动,需要分析货轮在平衡位置附近上下运动时, 它所受的合外力F与位移x间的关系,如果满足F=一kx,则货轮作简谐运动. 通过F=-x即可求得振动周期T=2π/w=2π√m及. 证货轮处于平衡状态时[图14-3(a)],浮力大小为F=mg.当船上下作 微小振动时,取货轮处于力平衡时的质心位置为坐标原点O,竖直向下为x轴 正向,如图14-3(b)所示.则当货轮向下偏移x位移时,受合外力为 EF=P+F 其中F为此时货轮所受浮力,其方向向上,大小为 F'=F+pgSx mg pgSx 则货轮所受合外力为 ZF P-F'=-pgS =-ka 式中=PgS是一常数.这表明货轮在其平衡位置上下所作的微小振动是简谐 运动. 由ΣF=md平xdz2可得货轮运动的微分方程为 d2xldt2+egSxlm =0 令w2=gSm,可得其振动周期为 T=2x/w=2r√m/pgS

14-4设地球是一个半径为R的均匀球体,密度p=5.5×103kg°m3.现 假定沿直径凿通一条隧道,若有一质量为m的质点在此 隧道内作无摩擦运动.(1)证明此质点的运动是简谐运 动;(2)计算其周期。 分析证明方法与上题相似.分析质点在隧道内运 动时的受力特征即可. 证(1)取图14-4所示坐标.当质量为m的质点 位于x处时,它受地球的引力为 F--Gmm 图14-4 式中G为引力常量,mz是以x为半径的球体质量,即 mx=4xoc33.令k=4 pGm/3,则质点受力 F=-4xGomx3 =-kx 因此,质点作简谐运动. (2)质点振动的周期为 T=2r√n/k=√3元G0 =5.07×103s

14-5如图14-5(a)所示,两个轻弹簧的劲度系数分别为k1、k2.当物体 在光滑斜面上振动时.(1)证明其运动仍是简谐运动;(2)求系统的振动频率. (8 (b) 立 7 (c) (d) 图14-5 分析从上两题的求解知道,要证明一个系统作简谐运动,首先要分析受力 情况,然后看是否满足简谐运动的受力特征(或简谐运动微分方程〉,为此,建立 如图14-5(b)所示的坐标.设系统平衡时物体所在位置为坐标原点0,Ox轴正 向沿斜面向下,由受力分析可知,沿Ox轴,物体受弹性力及重力分力的作用,其 中弹性力是变力.利用串联时各弹簧受力相等,分析物体在任一位置时受力与位 移的关系,即可证得物体作简谐运动,并可求出频率. 证设物体平衡时两弹簧伸长分别为x1、x2,则由物体受力平衡,有 mgsin 0=kix1=k2x2 (1) 按图(b)所取坐标,物体沿x轴移动位移x时,两弹簧又分别被拉伸x1和x2,即 x=x'1+x2则物体受力为 F mgsin 0-k2(x2+x2)=mgsin 6-k1(x1+x1) (2) 将式(1)代人式(2)得 F=-k2x2=-k1x1 (3) 由式(3)得x1=-F/1、x2=-F/兔2,而x=zi+x2,则得到 F=-(k1k2/k1+k2)x=-kx 式中=k1k2/(1+2)为常数,则物体作简谐运动,振动频率 y=a2m=2会云√展m=2x√1k21+2)m 讨论(1)由本题的求证可知,斜面领角日对弹簧是否作简谐运动以及振 动的频率均不产生影响.事实上,无论弹簧水平放置、斜置还是竖直悬挂,物体均 作简谐运动.而且可以证明它们的频率相同,均由弹簧振子的固有性质决定,这 就是称为固有频率的原因.(2)如果振动系统如图14-5(c)(弹簧并联)或如图 14-5()所示,也可通过物体在某一位置的受力分析得出其作简谐运动,且振动 缬率均为v=√欣1+2m,读者可以一试.通过这些例子可以知道,证明物 体是否作简谐运动的思路是相同的