
8-11964年,盖尔曼等人提出基本粒子是由更基本的夸克构成,中子就是 由一个带号e的上夸克和两个带-号。的下夸克构成.若将夸克作为经典粒子 处理(夸克线度约为10-0m),中子内的两个下夸克之间相距2.60×1015m. 求它们之间的斥力 解由于夸克可视为经典点电荷,由库仑定律 F=4型,点品=380 F与,方向相同表明它们之间为斥力

8一2质量为m,电荷为-的电子以圆轨道绕氢核旋转,其动能为Ek.证 明电子的旋转频率满足 2=32e6E me4 其中©0是真空电容率,电子的运动可视为遵守经典力学规律, 分桥根据题意将电子作为经典粒子处理.电子、氢核的大小约为10~15m, 轨道半径约为10~10m,故电子、氢核都可视作点电荷.点电荷间的库仑引力是 维持电子沿圆轨道运动的向心力,故有 1e2 m号=4o2 由此出发命题可证, 证由上述分析可得电子的动能为 E=im 12 8xE0 r 电子旋转角速度为 w2= e2 4πe0mr3 由上述两式消去r,得 y2= w2 32e6E
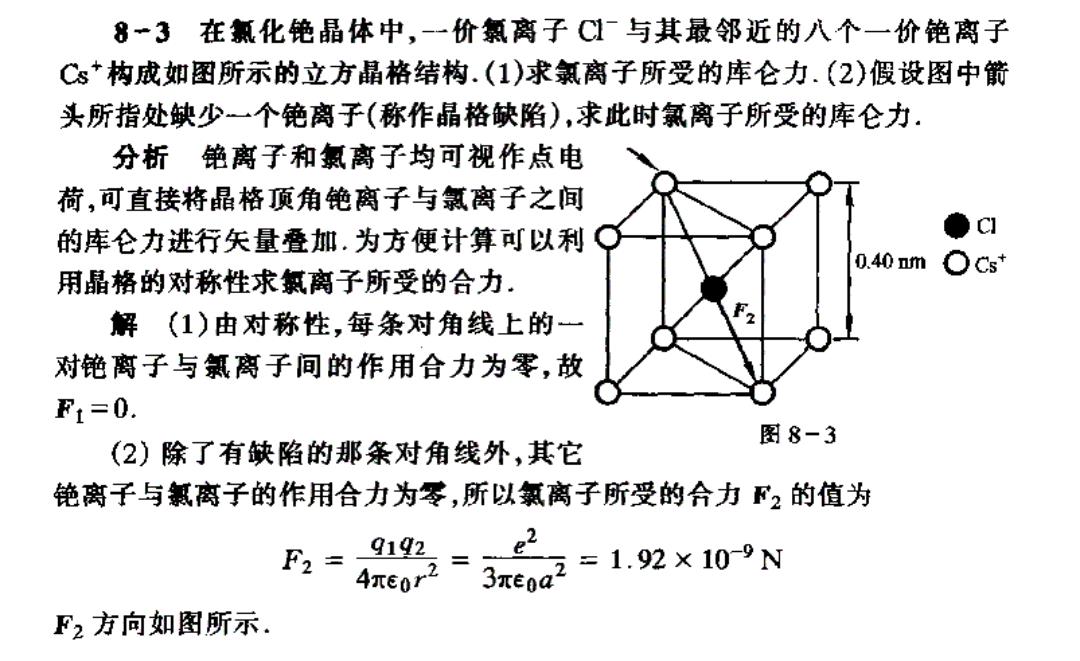
8一3在氯化铯晶体中,-一价氯离子C1与其最邻近的八个一价铯离子 Cs*构成如图所示的立方晶格结构.(1)求氯离子所受的库仑力.(2)假设图中箭 头所指处缺少一个铯离子(称作晶格缺陷),求此时氯离子所受的库仑力, 分析铯离子和氯离子均可视作点电 荷,可直接将晶格顶角铯离子与氯离子之间 的库仑力进行矢量叠加.为方便计算可以利。 ●C 0.40nm○Cs 用晶格的对称性求氯离子所受的合力。 解(1)由对称性,每条对角线上的一 对铯离子与氯离子间的作用合力为零,故 F1=0. 图8-3 (2)除了有缺陷的那条对角线外,其它 铯离子与氯离子的作用合力为苓,所以氯离子所受的合力F2的值为 F2=9192=e2 3xe0a2=1.92×10-9N F2方向如图所示

8一4两个点电荷所带电荷之和为Q,问它们各带电荷为多少时,相互间 的作用力最大? 分析这是一个条件极值问题.设其中一个点电荷带电q,则另一个点电荷 带电Q-g,因此它们间的库仑力F=F(g),由极值条件dF(g)/dg=0,可求得 最大作用力时它们各自的电荷. 解两点电荷之间的库仑力 Fa 由受值条件5=0,得 g=号Q 又幽 的一2x户<0,这表明两电街平分电荷Q时,它们之间的相互作用力 最大
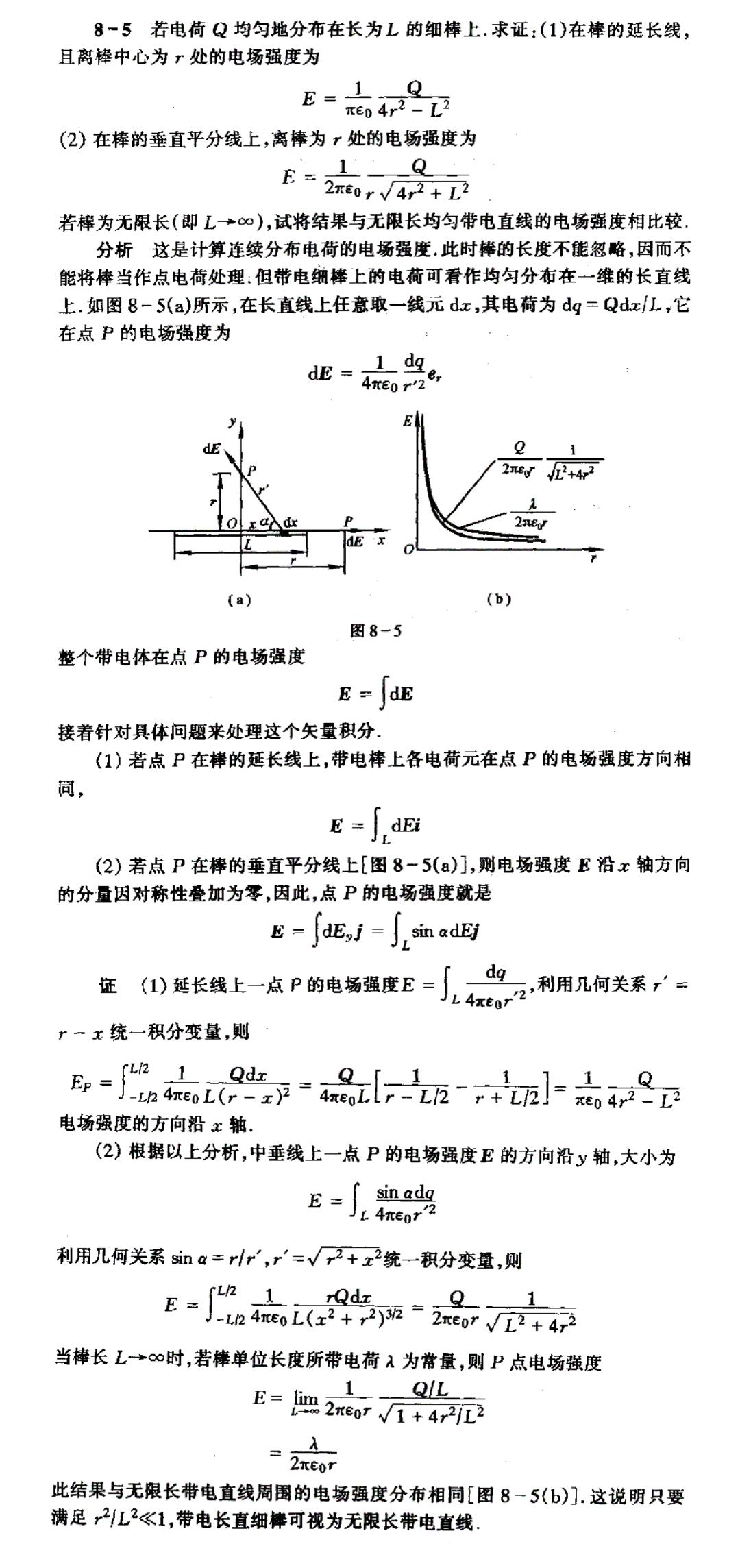
8-5若电荷Q均匀地分布在长为L的细棒上.求证:(1)在棒的延长线, 且离棒中心为r处的电场强度为 E=04r2-D Q (2)在棒的垂直平分线上,离棒为r处的电场强度为 0 E=20r√4r产+元 若棒为无限长(即L→∞),试将结果与无限长均匀带电直线的电场强度相比较 分析这是计算连续分布电荷的电场强度,此时棒的长度不能忽略,因而不 能将棒当作点电荷处理:但带电细棒上的电荷可看作均匀分布在一维的长直线 上.如图8-5(a)所示,在长直线上任意取一线元dx,其电荷为dg=Qdz/L,它 在点P的电场强度为 dE =Axeor' (a) (b) 图8-5 整个带电体在点P的电场强度 E=dE 接着针对具体问题来处理这个矢量积分. (1)若点P在棒的延长线上,带电棒上各电荷元在点P的电场强度方向相 同 E-dE (2)若点P在棒的垂直平分线上[图8-5(a)],则电场强度E沿x轴方向 的分量因对称性叠加为零,因此,点P的电场强度就是 E=JdE,1 sin adEj dg 在)鬓长线上-点P的电扬强度E=L利用几何类系了 r一x统一积分变量,则 -ia9u=品-tl8 电场强度的方向沿x轴。 (2)根据以上分析,中垂线上一点P的电场强度E的方向沿y轴,大小为 E=知当 利用几何关系s如a=rlr',r'=√2+z2统一积分变量,侧 E-n29“品/4 当棒长L→∞时,若棒单位长度所带电荷入为常量,则P点电场强度 QIL E=m2m0r1+4r元 二2x0r 此结果与无限长带电直线周围的电场强度分布相同[图8一5(b)].这说明只要 满足2L2《1,带电长直细棒可视为无限长带电直线