
9-1一真空二极管,其主要构件是一个半径R,=5.0×104m的圆柱形 阴极和一个套在阴极外,半径R2=4.5×10-3m的同轴圆筒形阳极.阳极电势 比阴极电势高300V,阴极与阳极的长度均为L=2.5×10~2m.假设电子从阴 极射出时的速度为等.求:(1)该电子到达阳极时所具有的动能和速率;(2)电子 剂从阳极射出时所受的力, 分析(1)由于半径R,《L,因此可将电极视作无限长2级 2R 圆柱面,阴极和阳极之间的电场其有轴对称性.从阴极射出 的电子在电场力作用下从静止开始加速,电子所获得的动能 等于电场力所作的功,也即等于电子势能的诚少,由此,可求 得电子到达阳极时的动能和速率. (2)计算阳极表面附近的电场强度,由F=q吧求出电 在两极表面所受的电场力, 解(1)电子到达阳极时,势能的减少量为 △Em=-eV=-4.8×10-7J 由于电子的初始速度为琴,故 图9-1 Ek-AEk=-△Ep=4.8×10-1J 因此电子到达阳极的速率为 /2应=1.03×102ms1 m (2)两极间的电场强度为 E=-2meore 两极间的电势差 负号表示阳极电势高于阴极电势,阴极表面电场强度 E=2a0R,='R 电子在阴极表面受力 F=-E=4.37×10-4e,N 这个力尽管很小,但作用在质量为9.11×10~31kg的电子上,电子获得的加速 度可达重力加速度的5×105倍

9-2一导体球半径为R1,外罩一半径为R2的同心薄导体球壳,外球壳 所带总电荷为Q,而内球的电势为V。,求此系统的电势和电场的分布 分析若V)二4红K,内球电势等于外球壳的电势,则外球壳内必定为等 Q 势体,电场强度处处为零,内球不带电. 若V≠4R,内球电势不等于外球壳电势,则外球完内电场强度不为 零,内球带电. 不失一般情况,假设内导体球带电q,导体达到静电平衡时电荷的分布如图 9-2所示.依照电荷的这一分布,利用高斯定理可求得 g+q 电场分布.并由V,=,E·dl或电势叠如求出电势的 分布.最后将电场强度和电势用已知量V、Q、R1、R2 表示. 解根据静电平衡时电荷的分布,可知电场分布呈 球对称.取同心球面为高斯面,由高斯定理中E·S=E (r)4πr2=∑q/0,根据不同半径的高斯面内的电荷分 图9-2 布,解得各区域内的电场分布为 r<R,时, E1(r)=0 R1<r<R2时, E,r)4 r>R2时, Es(r)=Q+g Axeor 由电场强度与电势的积分关系,可得各相应区域内的电势分布,r<R1时 Y=g·a-Edl++2d R Q 4xoR1+4xeoRz R,<7<R,时,V2-E·a=gdl+心Edl Q 0r+a8 >时,=6d=品 也可以从球面电势的叠加求电势的分布,在导体球内(r<R1) 0 在导体球和球壳之间(R1<r<R2) 0 Vadmcor4R 在球党外(r>R2)》 ⅓-8品 由题意 Vi=Vo=4xeoR*4RcoR 0 得 g=4enRM,-影Q 代人电场、电势的分布得 r<R1时,E1=0:V1=Vo R<<R时,a=BY-9,:-8业+9 4neoR2r r>R2时, E=+RQ,4=Ey,®2R9 2 4πe0R2r2 4πe0R2r

9-3在一半径为R1=6.0cm的金属球A外而套有一个同心的金属球壳 B.已知球壳B的内、外半径分别为R2=8.0cm,R3=10.0cm.设球A带有总电 荷QA=3.0×108C,球壳B带有总电荷Q8=2.0×10-8C.(1)求球壳B内、外 表面上所带的电荷以及球A和球壳B的电势;(2)将球壳B接地然后断开,再把 金属球A接地,求金属球A和球壳B内、外表面上所带的电荷以及球A和球壳 B的电势. 分析(1)根据静电感应和静电平衡时导体表面电荷分布的规律,电荷QA 均匀分布在球A表面,球壳B内表面带电荷-QA,外表面带电荷QB+QA,电 荷在导体表面均匀分布[图9-3()],由带电球面电势的叠加可求得球A和对 壳B的电势. (2)导体接地,表明导体与大地等电势(大地电势通常取为零).球壳B接地后 外表面的电荷与从大地流人的负电荷中和,球壳内表面带电-Q[图9-3(b)]. 断开球壳B的接地后,再将球A接地,此时球A的电势为零.电势的变化必 将引起电荷的重新分布,以保持导体的静电平衡.不失一般性可设此时球A带 电qA,根据静电平衡时导体上电荷的分布规律,可知球壳B内表面感应一qA,外 表面带电gA一QA[图9-3(c)].此时球A的电势可表示为 由VA=0可解出球A所带的电荷qA,再由带电球面电势的叠加,可求出球A和 球壳B的电势. O+O (a) (b) (c) 图9-3 解(1)由分析可知,球A的外表面带电3.0×108C,球壳B内表面带电 -3.0×108C,外表面带电5.0×10-8C.由电势的叠加,球A和球壳B的电势 分别为 V=8+ar,+8a8=5.6×10y (2)将球壳B接地后断开,再把球A接地,设球A带电9A,球A和球壳B 的电势为 V=4+a,+0点=0 -QA+9A 解得 RR2Q AR1R2+R2R-R1R3=2.12×108C 即球A外表面带电2.12×108C,由分析可推得球壳B内表面带电-2.12× 108C,外表面带电-0.9×10-8C.另外球A和球壳B的电势分别为 VA=0 Vg=-7.92×10V 导体的接地使各导体的电势分布发生变化,打破了原有的静电平衡,导体表 面的电荷将重新分布,以建立新的静电平衡

9-4三个平行导体板A、B和C的面积均为S,其中A板带电Q,B、C板 不带电,AB间相距为d1,A、C间相距为d2.求:(1)各导体板上的电荷分布和 导体板间的电势差.(2)将B、C两导体板分别接地,再求导体板上的电荷分布和 导体板间的电势差。 UC D a (b) (c) 图9-4 分析(1)首先分析静电平衡条件下,平行导体板表面电荷分布的规律.考 虑如图9一4(b)所示的一对平行导体板,取图中圆柱面为高斯面,高斯面的侧面 与电场强度E平行,电场强度通量为零:高斯面的两个端面在导体内部,因导体 内电场强度为零,因而电场强度通量也为零由高斯定理 E-ds=qleo=0 3q=0 上式表明处于静电平衡的平行导体板,相对的两个面应带等量异号电荷。 再利用叠加原理,导体板上四个带电面在导体内产生的合电场强度必须为 零,因而平行导体板外侧两个面带等量同号电荷. 依照上述分析,可求出导体板上各面的电荷分布和电势差, (2)B,C两导体板分别接地,VB=Vc=Uc=0.导体电势的改变将会引起 导体表面电荷的重新分布.电荷的分布依然应满足相对面等重异号:相背面等量 同号的规律;以使导体内部E二0,维持导体的静电平衡.根据电荷分布可确定 导体板间的电势差、 解(1)设电荷分布如图9-4(c)所示,依照静电平衡时导体板上电荷分布 规律,有 9B+9BR=0 9a+9cR=0 gAL QAR =Q qBL±qCR CBR =GAL GAR =9CL 解上述各式得 BL GAL QAR 9CR= q照=qa=-Q 故有 Vw2品 ve品 (2)B、C两导体接地,Uc=0,则有 [9BL=9CR=0 gAL gAR Q 9B欧=-9AL 9C.=-9AR 器41-器:=0 解上述各式得 dz 9BR=-9AL=- 4+,Q qC兰-AR=· 4a0 故有 U=-品。 UAc=didz soS dz+di
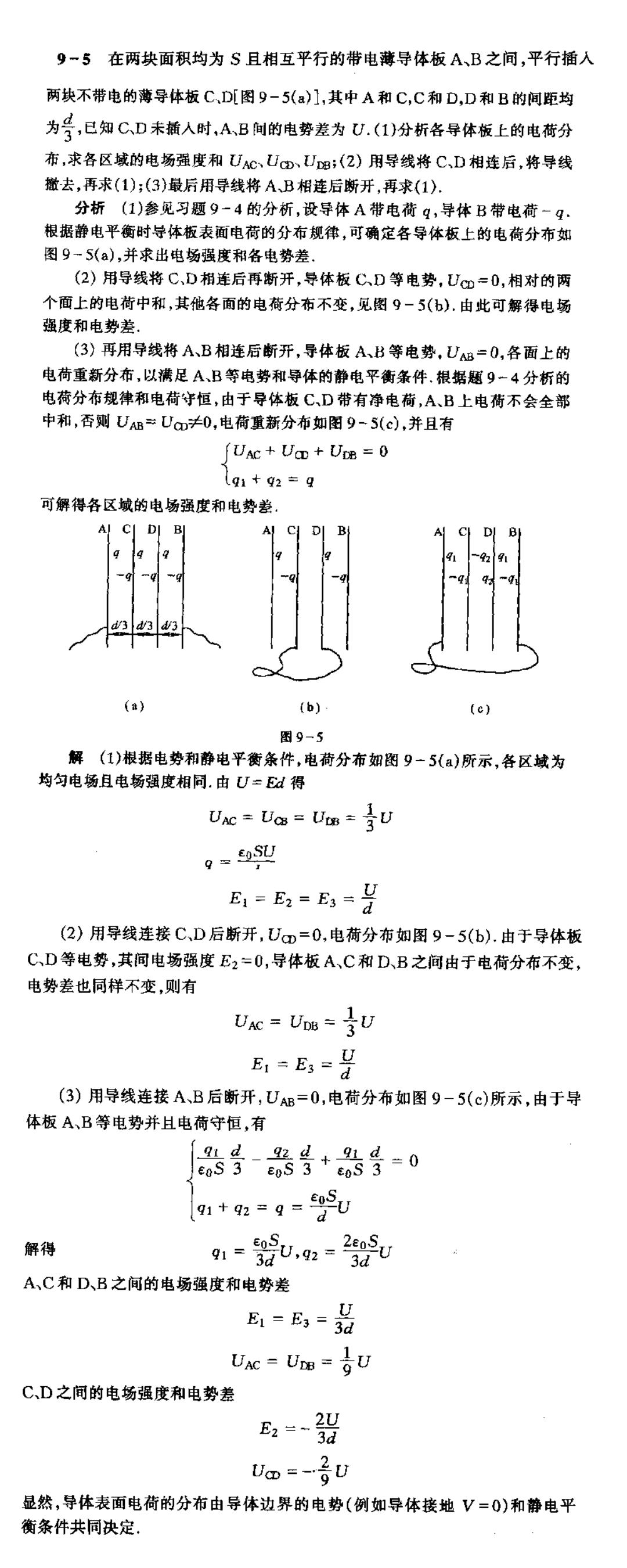
9一5在两块面积均为S且相互平行的带电薄导体板A、B之间,平行插人 两块不带电的薄导体板C,D[图9-5(a)],其中A和C,C和D,D和B的间距均 为号,已知CD未插入时,A、B间的电势差为U.(1)分析各导体饭上的电荷分 布,求各区域的电场强度和UCUD、Um;(2)用导线将C,D相连后,将导线 撇去,再求(1):(3)最后用导线将A、B相连后断开,再求(1) 分析(1)参见习题9-4的分析,设导体A带电荷g,导体B带电荷一g. 根据静电平衡时导体板表面电荷的分布规律,可确定各导体板上的电荷分布如 图9-5(a),并求出电场强度和各电势差. (2)用导线将C、D相连后再断开,导体板CD等电势,Um=0,相对的两 个面上的电荷中和,其他各面的电荷分布不变,见图9一5(b).由此可解得电场 强度和电势差, (3)再用导线将A、B相连后断开,导体板A、B等电势,UB=0,各面上的 电荷重新分布,以满足AB等电势和导体的静电平衡条件.根据题9-4分析的 电荷分布规律和电荷守恒,由于导体板C、D带有净电荷,AB上电荷不会全部 中和,否则UB÷Uam≠0,电荷重新分布如图9-5(c),并且有 ∫UAc+UD+UoB=0 q1+q2-9 可解得各区城的电场强度和电势差。 C 33 (a) (b) (c) 图9-5 解(1)根据电势和静电平衡条件,电荷分布如图9一5(a)所示,各区域为 均匀电场且电扬强度相同.由U=Ed得 Uc=Ucs=U=青U 9✉9.SV E=E=B3=当 (2)用导缇连接CD后断开,Um=0,电荷分布如图9-5(b.由于导体板 C、D等电势,其间电场强度E2=0,导体板A、C和D、B之间由于电荷分布不变, 电势差也同样不变,则有 UAC UDB=U E1=E= (3)用导线连接AB后断开,UB=0,电荷分布如图9-5(c)所示,由于导 体板A、B等电势并且电荷守恒,有 器号-器号+器号-0 91+92=9=U 解得 91=2,92=20 A、C和D、B之间的电场强度和电势差 B=E=品 Uae=UB=号U C、D之间的电场强度和电势差 =-器 Uam=-子U 显然,导体表面电荷的分布由导体边界的电势(例如导体接地V=0)和静电平 衡条件共同决定