第十四章波动 14-一横波再沿绳子传福时得被动方程为y=020m)c©2.5题r-(m'江·(1)求装得挥 解、波速、频率及波长:(2)求绳上质点氟动时海最大速度:(3)分别通出=s和2s时得波 彩,并指出被峰和该容,西出x0m处质点得振动曲规并对论其与波形图得不可, fm 12 14-ly-0.20m)eo2.5s-(am' 分析(1)已知被动方程(又称波函数)求被动的籍征量(波速m、顿率?、振幅A及 被长等),通常采用比较法。将已知的波动方程按波动方程的一般形式 一4叫代}风书写。丝后通过比数镜定各特征最(试中前一、“十“的选取分 别对应波沿x轴正向和负向传播)。比较法思路清晰、求解简便,是一种常用的解题方法。 (2)讨论液动问题,要理解据动物理量与被动物理量之间的内在联系与区别,例如区分质 点的振动速度与波速的不月,振动速度是质点的运动速度,即,一/仙:而波速是波线上质 点运动状态的传播速度(也称相位的传播速度,波形的传疆速度成能量的传播速度),其大 小由介质的性质读定。介质不变,被速保持恒定。(3》将不同时的1值代人已知波动方程, 使可以得到不同时刻的波形方程y=),从而作出波形图。而将确定的重植代入波动方程, 便可以得到该位置处质点的运动方程y一),从面作出振动图。 解(1)将已知被动方程表示为 y=(020mc2.5sk-/2.5m3】 与一般表达式y=Ac-x/)+%]比较,可得 A=020m,F=25m-8%=0 则v=台2x=125b,=y=20网 〔2)绳上质点的振动速度 v=h=bsm人n形5ak-x/25ws 则n=157限5 (3》=1s和1=2s时的波形方程分别为 y=020m)e0中5g-(am月 为=020m)e04x-m
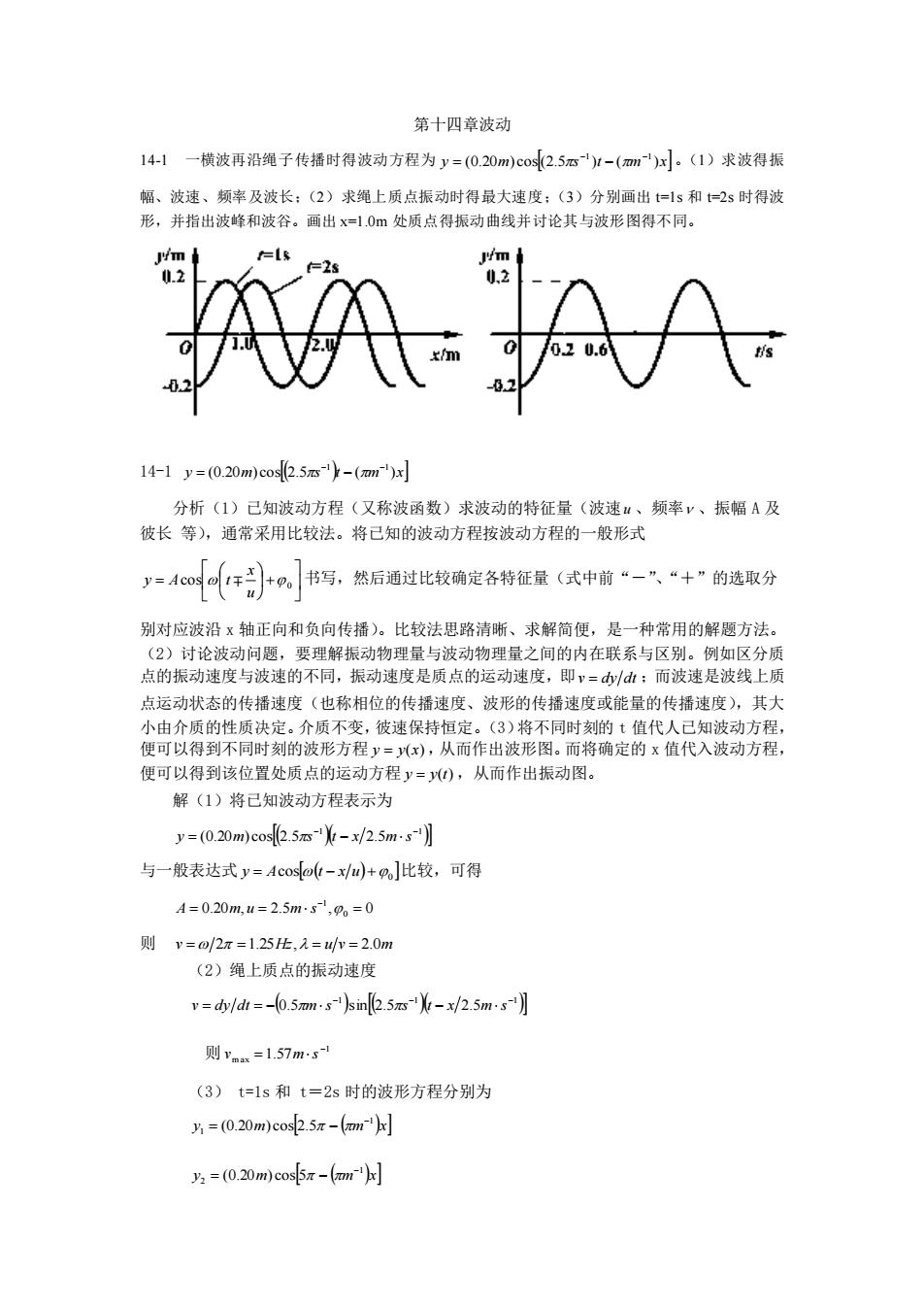
第十四章波动 14-1 一横波再沿绳子传播时得波动方程为 y (0.20m) cos(2.5 s )t ( m )x −1 −1 = − 。(1)求波得振 幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出 t=1s 和 t=2s 时得波 形,并指出波峰和波谷。画出 x=1.0m 处质点得振动曲线并讨论其与波形图得不同。 14-1 y (0.20m) cos(2.5 s )t ( m )x −1 −1 = − 分析(1)已知波动方程(又称波函数)求波动的特征量(波速 u 、频率 、振幅 A 及 彼长 等),通常采用比较法。将已知的波动方程按波动方程的一般形式 + = 0 cos u x y A t 书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分 别对应波沿 x 轴正向和负向传播)。比较法思路清晰、求解简便,是一种常用的解题方法。 (2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。例如区分质 点的振动速度与波速的不同,振动速度是质点的运动速度,即 v = dy dt ;而波速是波线上质 点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大 小由介质的性质决定。介质不变,彼速保持恒定。(3)将不同时刻的 t 值代人已知波动方程, 便可以得到不同时刻的波形方程 y = y(x) ,从而作出波形图。而将确定的 x 值代入波动方程, 便可以得到该位置处质点的运动方程 y = y(t) ,从而作出振动图。 解(1)将已知波动方程表示为 ( )( ) 1 1 (0.20 ) cos 2.5 2.5 − − y = m s t − x ms 与一般表达式 ( ) 0 y = Acos t − x u + 比较,可得 0.20 , 2.5 , 0 0 1 = = = − A m u m s 则 v = 2 =1.25Hz, = u v = 2.0m (2)绳上质点的振动速度 ( ) ( )( ) 1 1 1 0.5 sin 2.5 2.5 − − − v = dy dt = − ms s t − x ms 则 1 m ax 1.57 − v = ms (3) t=1s 和 t=2s 时的波形方程分别为 y m ( m )x 1 1 (0.20 ) cos 2.5 − = − y m ( m )x 1 2 (0.20 ) cos 5 − = −

波形图如图14一1《a)所示. x一1.0阳处质点的运动方程为 y=-(0.20m)cos(2.5) 振动图线如图14一1(6》所示。 被彩图与据动图虽在图形上相似,但却有着本质的区别前者表示某确定时波钱上所有 质点的位移情况,而后者测表示某确定位置的时间变化的情况。 14-2被酒作简请运动,其运动方程为y=(4.0×0mos20酒W,它所形成得被形以30m的 的速度沿一直线传福。(1)求波的周期及波长:《2》写出波的方程。 14-2y-(40x10-3wmc0s20ar 分析已知被源运动方程求被动物理量及被动方程,可先将运动方程与其一般形式 y■A0s叶+民)进行比较,求出根幅地角频率。及初相民,而这三个物理量与被动方程的 一般形式y=Aeo叶-+]中相应的三个物理量是相同的。再利用盟中己知的该速U 及公式o-2Y=2x/了和2=uT即可求解. 解(1)由己知的运动方程可知。质点霰动的角频率四=240✉,根据分析中所述,被 的周期就是振动的圆期,故有 T=2x/世=833x1x 波长为 =NT =025m (2)将已知的被源运动方程与简谐运动方程的一般形式比较后可得 A=4.0×10m,=20m,网=0 故以波源为原点,沿X轴正向传播的波的波动方程为 y=Acosol-x/u)+ =(40×10'刚c0520s'M-(&m'xl 143以如以波动方程为y=(0.05周)s0西M-(2m·《1)求被长、赖率、波速和周期: (2)说明0时方程的意义,并作图表不。 v/m 0.05 01 14-3y=0.08m)sin0gr-2w] 分析紧用比较法。将题给的被动方程改写成被动方程的象弦函数形式,比较可得角赖率
波形图如图 14-1(a)所示。 x=1.0m 处质点的运动方程为 y m ( s )t 1 (0.20 ) cos 2.5 − = − 振动图线如图 14-1(b)所示。 波形图与振动图虽在图形上相似,但却有着本质的区别前者表示某确定时刻波线上所有 质点的位移情况,而后者则表示某确定位置的时间变化的情况。 14-2 波源作简谐运动,其运动方程为 y (4.0 10 m)cos(240 s )t −3 −1 = ,它所形成得波形以 30m/s 的速度沿一直线传播。(1)求波的周期及波长;(2)写出波的方程。 14-2 y (4.0 10 m) cos(240 s )t −3 −1 = 分析 已知彼源运动方程求波动物理量及波动方程,可先将运动方程与其一般形式 ( ) 0 y = Acos t + 进行比较,求出振幅地角频率 及初相 0 ,而这三个物理量与波动方程的 一般形式 ( ) 0 y = Acos t − x u + 中相应的三个物理量是相同的。再利用题中已知的波速 U 及公式 = 2 = 2 /T 和 = uT 即可求解。 解(1)由已知的运动方程可知,质点振动的角频率 1 240 − = s 。根据分析中所述,波 的周期就是振动的周期,故有 T s 3 2 / 8.33 10− = = 波长为 = uT = 0.25m (2)将已知的波源运动方程与简谐运动方程的一般形式比较后可得 4.0 10 240 0 0 3 1 = = = − − A m, s , 故以波源为原点,沿 X 轴正向传播的波的波动方程为 ( ) (4.0 10 ) cos[(240 ) (8 ) ] cos 3 1 1 0 m s t m x y A t x u − − − = − = − + 14-3 以知以波动方程为 (0.05 )sin[(10 ) (2 ) ] 1 1 y m s t m x − − = − 。(1)求波长、频率、波速和周期; (2)说明 x=0 时方程的意义,并作图表示。 14-3 (0.05 )sin[(10 ) (2 ) ] 1 1 y m s t m x − − = − 分析采用比较法。将题给的波动方程改写成波动方程的余弦函数形式,比较可得角频率

波速山,从而求出波长、频率等。当x确定封波动方程即为质点的运动方程y一): 解(1》将题给的波动方程改写为 y=006mnw们0e-x/5m·-g/2到 与y-Ace-+%]比较后可得波速角规率g-10s',放有 =t/2x=50t,T=1/r=02x,2=wT=34m (2)由分析知x=0时,方程表示位于坐标源点的质点的运动方程(图13一4)。 y-(0.05m)ecs00ag-x/2] 144被要作简请银动,周期为002s,看该醒动以100ms的速度传播,设10时,波潭处的质 点经平衡位置向正方向运动,求:(1》距离被源15,0m和50m两处质点的运动方程和初相:(2) 距离波源160m和70m两处妩点的相位差。 14-4 分析(1)根据题意先设法写出波动方程,然后代人确定点处的坐标,即得到质点的运动方 程。并可求得据动的初相。(2)波的传播也可以看成是相位的传播。由波长A的物理含意, 可知波线上任两点间的相位差为△g=24x/A。 解(1》由题给条件T-0.02s,u一100n·s一1,可得 =2r/T=100g1A=T=2m 当=0时,被源质点经平衡位置向正方向运动,因而由旋转矢量法可得该质点的初 相为民=-2或3缸/2)。若以波源为坐标原点,测波动方程为 y=c0s00s1-x/100ms)-g/2 距波源为x=15.0加和=5,0加处质点的运动方程分别为 片-Ac0sW1DsM-15.5g] 为=4 cosK100sM-5.5r] 它门的初相分别为%,=-15.5和=-55行〔若被源初相取,=3知/2,则初相 4p=g-%-23-黑)/2=夏,.) (2)距被源160■和17.0■两点间的相位差 4p■鸭-%3■2黑-名)/A■累 143被夏作简普根动,周期为10×10s,以它经平衡位置句正方询运动时为时间足点,若此 丽功以一40Om的连度沿直线传播,求,《1》距离被源80幽处质点P的运动方程和初相:(2) 离被单90m和100m处两点的相位差, 14-5 解分析月上题。在确知角频率9=2r/T=200o、波连#=400m·和初相 %=3r/2或-x/2》的条件下,被动方程 y=Ac0s200酒t-x/0m·)+3r/2] 位于斯=80■处,质点P的运动方程为 y.Acos[200m'-5e/2]
波速 U,从而求出波长、频率等。当 x 确定时波动方程即为质点的运动方程 y = y(t) 。 解(1)将题给的波动方程改写为 (0.05 )sin[(10 )( / 5 ) / 2] 1 1 = − − − − y m s t x m s 与 ( ) 0 y = Acos t − x u + 比较后可得波速 角频率 1 10 − = s ,故有 = / 2 = 5.0Hz,T =1/ = 0.2s, = uT = 3.14m (2)由分析知 x=0 时,方程表示位于坐标原点的质点的运动方程(图 13—4)。 (0.05 ) cos[(10 ) / 2] 1 = − − y m s t 14-4 波源作简谐振动,周期为 0.02s,若该振动以 100m/s 的速度传播,设 t=0 时,波源处的质 点经平衡位置向正方向运动,求:(1)距离波源 15.0m 和 5.0m 两处质点的运动方程和初相;(2) 距离波源 16.0m 和 17.0m 两处质点的相位差。 14-4 分析(1)根据题意先设法写出波动方程,然后代人确定点处的坐标,即得到质点的运动方 程。并可求得振动的初相。(2)波的传播也可以看成是相位的传播。由波长 A 的物理含意, 可知波线上任两点间的相位差为 = 2x / 。 解(1)由题给条件 T=0.02 s,u=100 m·s-l,可得 2 /T 100 s uT 2m 1 = = = = − ; 当 t=0 时,波源质点经平衡位置向正方向运动,因而由旋转矢量法可得该质点的初 相为 0 = − / 2(或3 / 2) 。若以波源为坐标原点,则波动方程为 cos[(100 )( /100 ) / 2] 1 1 = − − − − y A s t x m s 距波源为 x1=15.0m 和 x2=5.0m 处质点的运动方程分别为 cos[(100 ) 15.5 ] 1 1 = − − y A s t cos[(100 ) 5.5 ] 1 2 = − − y A s t 它们的初相分别为 10 = −15.5和20 = −5.5 (若波源初相取 0 = 3 / 2 ,则初相 =1 −2 = 2(x2 − x1 )/ = ,。) (2)距波源 16.0 m 和 17.0 m 两点间的相位差 =1 − 2 = 2 (x1 − x2 ) / = 14-5 波源作简谐振动,周期为 1.0×10-2 s,以它经平衡位置向正方向运动时为时间起点,若此 振动以 u=400m/s 的速度沿直线传播。求:(1)距离波源 8.0m 处质点 P 的运动方程和初相;(2) 距离波源 9.0m 和 10.0m 处两点的相位差。 14-5 解分析同上题。在确知角频率 1 2 / 200 − = T = s 、波速 1 400 − u = ms 和初相 0 = 3 / 2(或− / 2) 的条件下,波动方程 cos[(200 )( / 400 ) 3 / 2] 1 1 = − + − − y A s t x m s 位于 xP =8.0 m 处,质点 P 的运动方程为 cos[(200 )( 5 / 2] 1 = − − y A s t p

该质点叛动的初相pm·-5r/2。而距波源9,0■和100■两点的相位差为 p=2无3-x)/A=2到3-无/T=R/2 如果波源初相取钱一一潭/2,则波动方程为 y=Ac0s200s1-9r/2 质点P振动的初相也变为=一9x/2,但被线上任两点间的相位差并不改变。 146有一平面简谐波在介质中传播,波速-100ms,波线上右侧距波源0(坐标厚点)为75.0m 处的一点P的运动方程为男,=00啊)sC。N+x2到.求(1)被向x轴正方向传播时的被 动方程:(2)》被向x拍负方向传播时的被动方程。 P 0 0 b】 14-6y,-(0.30m)cos0sy+g/2 分析在已知波线上某点运动方程的条件下,建立被动方程时常采用下面两种方法:(1) 先写出以波源0为源点的波动方程的一最形式,然后利用己知点P的运动方程米确定该波动 方程中各量,从而建立所求波动方程。(2)建立以点P为原点的波动方程,由它来确定波源 点0的运动方程,从而可得出以波源点0为源点的波动方程。 解1(1)设以波源为原点0。沿X轴正向传播的波动方程为 y=Acos(t-x/u) 将u一100■·s一“代人,且取x二75■得点P的运动方程为 ,=Acol-0.75+%】 与题意中点P的运动方程比较可得A一0.30阳,0=2容、%。=2,则所求被动方程为 多,=030mje0s0s'0-x/100m-月 (2当沿怎轴负向传播时,被动方程为 y=AcoW+对+】 将x-75■、m-100阳代人后,与题给点P的运动方程比较得A=0.30如、信=2西、 两,=-,测所求波动方程为 y=030m0O5K2s1+x/00m~s-] 解2(1)如图14一6(a)所示,取点P为坐标照点0',沿0”x轴向右的方 向为正方向。根据分析,当被沿该正方向传播时,由点P的运动方程,可得出以 0'(即点P)为星点的被动方程为 y=030m)60s21=x/10m)+05
该质点振动的初相 P0 = −5 / 2 。而距波源 9.0 m 和 10.0 m 两点的相位差为 = 2(x2 − x1 )/ = 2(x2 − x1 )/ uT = / 2 如果波源初相取 0 = − / 2 ,则波动方程为 cos[(200 )( 9 / 2] 1 = − − y A s t 质点 P 振动的初相也变为 P0 = −9 / 2 ,但波线上任两点间的相位差并不改变。 14-6 有一平面简谐波在介质中传播,波速 u=100m/s,波线上右侧距波源 O(坐标原点)为 75.0m 处的一点 P 的运动方程为 (0.30 )cos[(2 ) / 2] 1 = + − y m s t p 。求(1)波向 x 轴正方向传播时的波 动方程;(2)波向 x 轴负方向传播时的波动方程。 14-6 (0.30 )cos[(2 ) / 2] 1 = + − y m s t p 分析在已知波线上某点运动方程的条件下,建立波动方程时常采用下面两种方法:(1) 先写出以波源 O 为原点的波动方程的一般形式,然后利用已知点 P 的运动方程来确定该波动 方程中各量,从而建立所求波动方程。(2)建立以点 P 为原点的波动方程,由它来确定波源 点 O 的运动方程,从而可得出以波源点 O 为原点的波动方程。 解 1(1)设以波源为原点 O,沿 X 轴正向传播的波动方程为 ( ) 0 y = Acos t − x u + 将 u=100 m·s-‘代人,且取 x 二 75 m 得点 P 的运动方程为 ( ) 75 0 y p = Acos t − 0. s + 与题意中点 P 的运动方程比较可得 A=0.30m、 1 2 − = s 、 0 = 2 。则所求波动方程为 (0.30 )cos[(2 )( /100 )] −1 −1 y = m s t − x ms p (2)当沿 X 轴负向传播时,波动方程为 ( ) 0 y = Acos t + x u + 将 x=75 m、 1 100 − u = ms 代人后,与题给点 P 的运动方程比较得 A= 0.30m、 1 2 − = s 、 0 = − ,则所求波动方程为 (0.30 ) cos[(2 )( /100 ) ] 1 1 = + − − − y m s t x m s 解 2(1)如图 14 一 6(a)所示,取点 P 为坐标原点 O’,沿 O’x 轴向右的方 向为正方向。根据分析,当波沿该正方向传播时,由点 P 的运动方程,可得出以 O’(即点 P)为原点的波动方程为 (0.30 ) cos[(2 )( /100 ) 0.5 ] 1 1 = − + − − y m s t x m s
将x一5■代入上式,可得点0的运动方程为 yo =(030m)cosQes)r 由此可写出以点D为坐标原点的波动方程为 y=030网e0sW28X1-言/00m·s月 (2)当波沿河X轴负方向传播时。如图14一6(b》所示,仍先写出以0°(即点P) 为原点的波动方程 y=00w)0s2打(+x/100m·s)+0.5知 将x=-5■代人上式,可得点0的运动方程为 a-0.30m)esl2a'-] 则以点0为原点的波动方程为 y=(0.30周)c0s2石X1+x/100周~3)-x] 讨论对于平面简带被来说,如果已知波线上一点的运动方程,求另外一点的运动方程, 也可用下述方法米处理:波的传播是振动状态的传播,浅线上各点(包括星点)是重复泼 源质点的振动状态,只是初相位不同而已。在己知某点初相平0的前提下,根据两点间的相 位差4p=鸟-%-2x/2,即可确定未知点的初相中小 14-7图147为平面简谐液在0时的波形图。设此简谐波的频率为250Hx。且此时图中质点P 的运动方向向上,滚:《1)该波的被动方程:(2》在是原点0为T5m处蘭点的蹈动方程与0 时该点的服功速度。 /m 0.10 10.0am 14-7 分析(1)从波形由线图铁取波的特征量。从而写出波动方程是建立波动方程的又一逢 径。具体步露为:L.从波形图得出被长、扳幅A和波速山一加:2.根据点P的运动趋势 米判斯被的传播方向。从而可确定原点处质点的运动趋向,并利用靛转关量法雨定其初相 气·(2)在泼动方程确定后,即可得到波线上距原点0为x处的运动方程y=y(t)》,及该 质点的据动速度v一dy/dt, 解(1》从图15-8中得知,波的辰幅A=010m,波长2-20.0m,则波速 w=v=5.0x0ms。根据t-0时点P白上运动,可知被沿0x轴负向传播,并判定时 位于单点处的质点将沿0,轴负方向运动,利用能转矢量法可得其初相%=常3。故被动方 程为
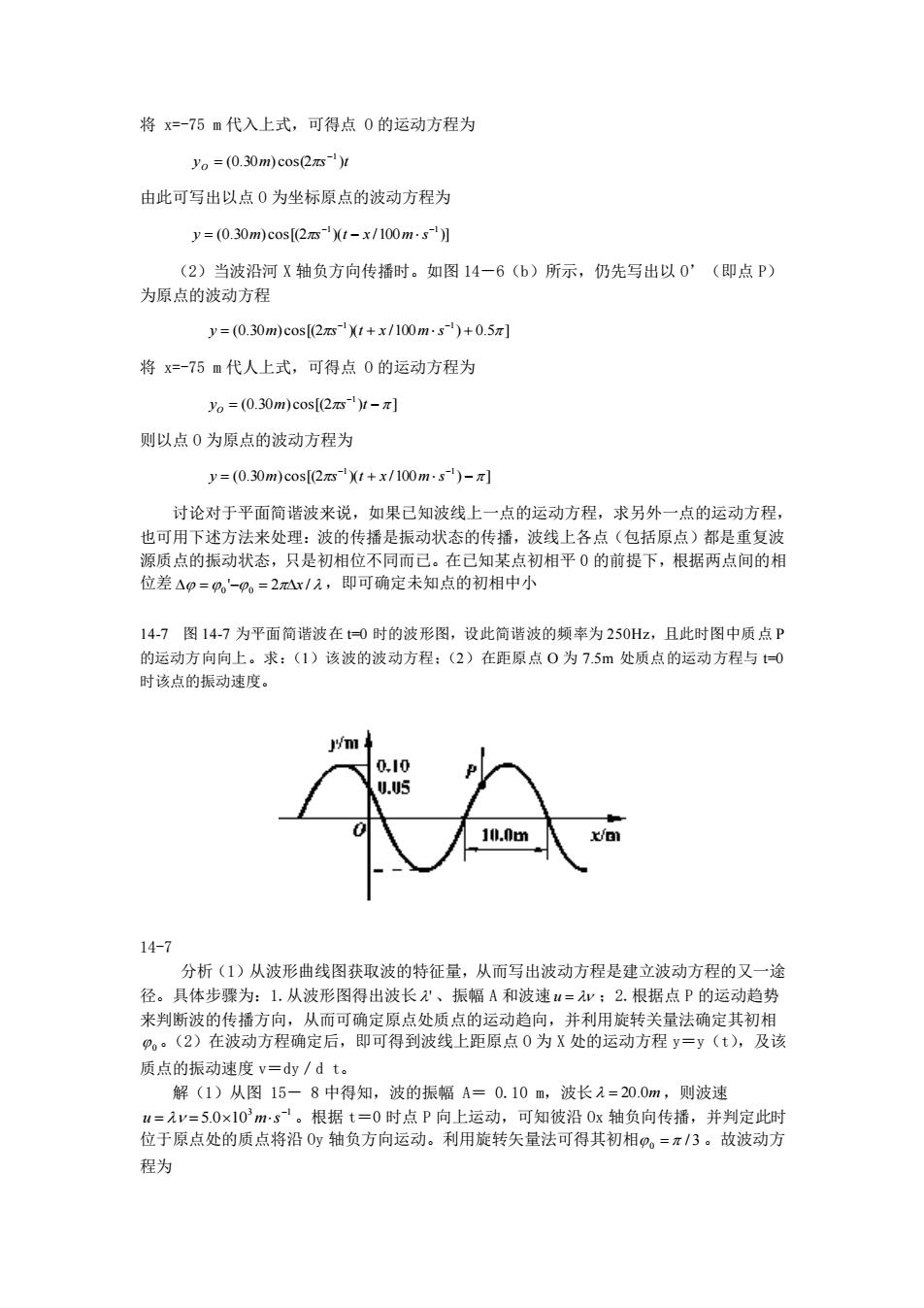
将 x=-75 m 代入上式,可得点 O 的运动方程为 y m s t O (0.30 ) cos(2 ) −1 = 由此可写出以点 O 为坐标原点的波动方程为 (0.30 ) cos[(2 )( /100 )] −1 −1 y = m s t − x ms (2)当波沿河 X 轴负方向传播时。如图 14-6(b)所示,仍先写出以 O’(即点 P) 为原点的波动方程 (0.30 ) cos[(2 )( /100 ) 0.5 ] 1 1 = + + − − y m s t x m s 将 x=-75 m 代人上式,可得点 O 的运动方程为 (0.30 ) cos[(2 ) ] 1 = − − y m s t O 则以点 O 为原点的波动方程为 (0.30 ) cos[(2 )( /100 ) ] 1 1 = + − − − y m s t x m s 讨论对于平面简谐波来说,如果已知波线上一点的运动方程,求另外一点的运动方程, 也可用下述方法来处理:波的传播是振动状态的传播,波线上各点(包括原点)都是重复波 源质点的振动状态,只是初相位不同而已。在已知某点初相平 0 的前提下,根据两点间的相 位差 =0 '−0 = 2x / ,即可确定未知点的初相中小 14-7 图 14-7 为平面简谐波在 t=0 时的波形图,设此简谐波的频率为 250Hz,且此时图中质点 P 的运动方向向上。求:(1)该波的波动方程;(2)在距原点 O 为 7.5m 处质点的运动方程与 t=0 时该点的振动速度。 14-7 分析(1)从波形曲线图获取波的特征量,从而写出波动方程是建立波动方程的又一途 径。具体步骤为:1.从波形图得出波长 ' 、振幅 A 和波速 u = ;2.根据点 P 的运动趋势 来判断波的传播方向,从而可确定原点处质点的运动趋向,并利用旋转关量法确定其初相 0 。(2)在波动方程确定后,即可得到波线上距原点 O 为 X 处的运动方程 y=y(t),及该 质点的振动速度 v=dy/d t。 解(1)从图 15- 8 中得知,波的振幅 A= 0.10 m,波长 = 20.0m ,则波速 3 1 5.0 10 − u = = ms 。根据 t=0 时点 P 向上运动,可知彼沿 Ox 轴负向传播,并判定此时 位于原点处的质点将沿 Oy 轴负方向运动。利用旋转矢量法可得其初相 0 = / 3 。故波动方 程为