华东理工大学：《线性代数》课程电子教案（PPT课件）第一章 矩阵

例1 设 已知A=B,求x,y,z. 解 ·A=B, .x=2,y=3,z=2 上页 区回

例1 设 , 1 1 3 , 3 1 2 1 2 3        =      = y z x A B 已知 A = B,求 x, y, z. 解  A = B,  x = 2, y = 3, z = 2

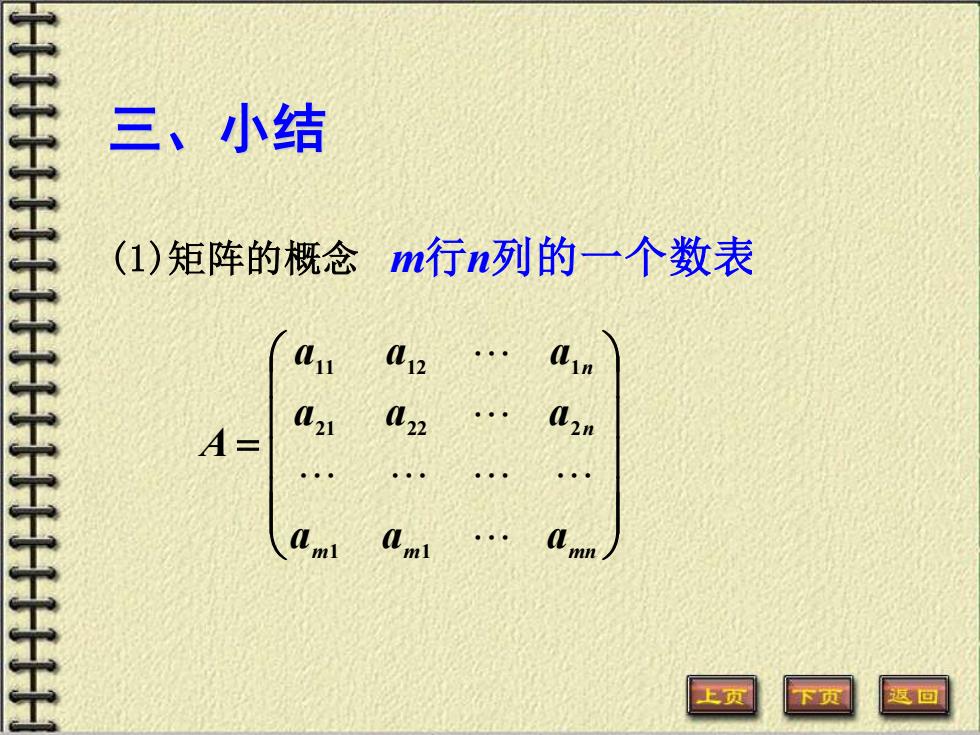
三、小结 (1)矩阵的概念m行n列的一个数表 Az l22 A- 上页

三、小结 (1)矩阵的概念               = m m mn n n a a a a a a a a a A        1 1 21 22 2 11 12 1 m行n列的一个数表

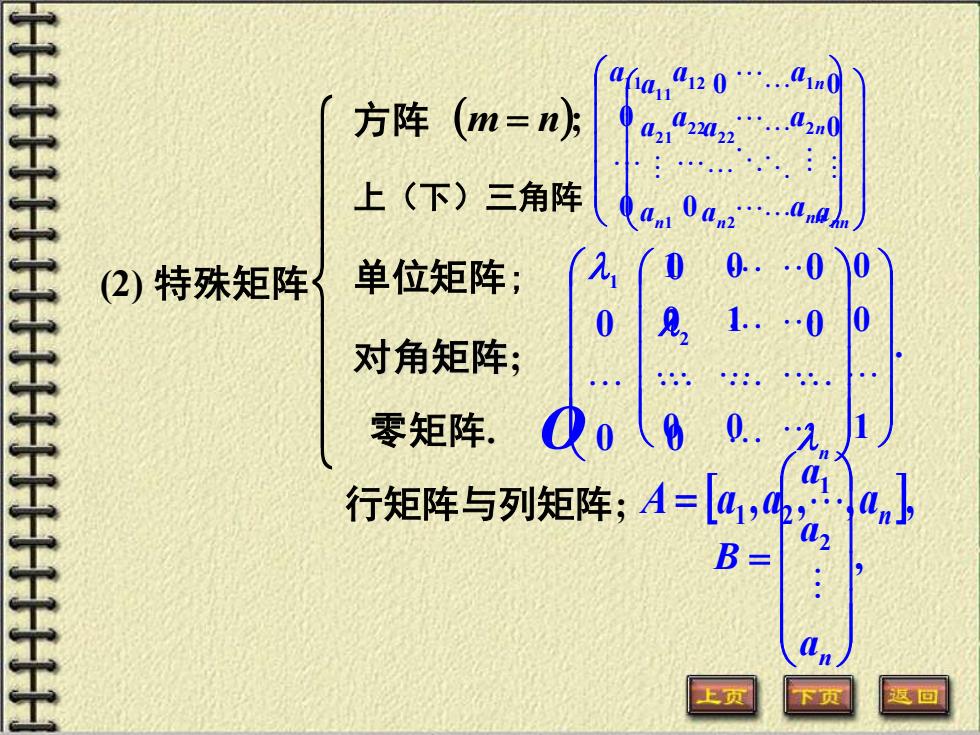
方阵(m=n 上（下）三角阵 (2)特殊矩阵 单位矩阵； 1. 对角矩阵； 零矩阵 0. 行矩阵与列矩阵；A=[41,, a,b B 上页 返回

(2) 特殊矩阵        方阵 (m = n); 上（下）三角阵 单位矩阵; 对角矩阵; 零矩阵. . 0 0 1 0 1 0 1 0 0                      , 2 1               = an a a B   , , , , 1 2 n A = a a  a                n          0 0 0 0 0 0 2 1 行矩阵与列矩阵;               an an ann a a a        1 2 21 22 11 0 0 0               nn n n a a a a a a        0 0 0 22 2 11 12 1 O

思考题 一 维矩阵[-1]是否等于数-1？ 思考题解答 是的！ 王页 下页 区回

思考题 一维矩阵 − 1是否等于数 − 1？ 思考题解答 是的！

第一季短阵 第二节 矩阵的运算 一、 矩阵的加法 二、 数乘矩阵 三、矩阵与矩阵相乘 四、矩阵的转置运算 五、小结、思考题

第二节 矩阵的运算 第一章 矩阵 一、矩阵的加法 二、数乘矩阵 三、矩阵与矩阵相乘 四、矩阵的转置运算 五、小结、思考题