华东理工大学：《线性代数》课程电子教案（PPT课件）第一章 矩阵

只有一列元素的矩阵 B= 称为列矩阵（或列向量） 2 2 21 (3)形如 即主对角线以下元素 全为零的方阵称为上三角矩阵。 页

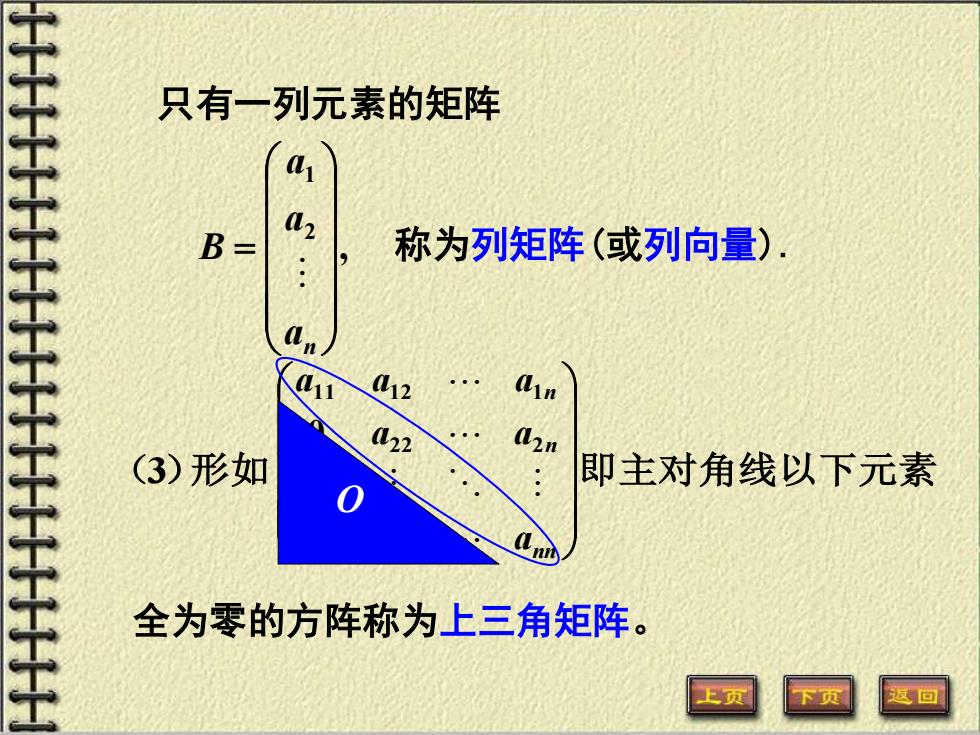
只有一列元素的矩阵 , 2 1               = an a a B  称为列矩阵(或列向量). 全为零的方阵称为上三角矩阵。 （3）形如 即主对角线以下元素               nn n n a a a a a a        0 0 0 22 2 11 12 1 O

形如 022 即主对角线以上元素 0n2 全为零的方阵称为下三角矩阵。 (4)既是上三角又是下三角矩阵的方阵，即 形如 的方阵，称为对角矩阵 (或对角阵). 记作 A=diaglA,A 回

称为对角矩阵 (或对角阵）. （4）                n          0 0 0 0 0 0 2 1 形如 的方阵, O O 全为零的方阵称为下三角矩阵。 形如 即主对角线以上元素               an an ann a a a        1 2 21 22 11 0 0 0 O 既是上三角又是下三角矩阵的方阵，即 记作 [ , , , ]. A = diag 1 2   n

(⑤)数（纯）量矩阵（标量矩阵） a 0 0 0 0 a 0 0 称对角线元相等的对角矩阵 为数量矩阵或标量阵。 00 0 当a=1时，记作 I=I 全为1 称为单位矩阵（或单位阵），有时也记作E

(5) 数(纯)量矩阵（标量矩阵）               = = 0 0 1 0 1 0 1 0 0        n I I 称为单位矩阵（或单位阵）.有时也记作E. O O 全为1 称对角线元相等的对角矩阵 为数量矩阵或标量阵。               a a a 0 0 0 0 0 0 0 0 0     当 a = 1 时，记作

(6)元素全为零的矩阵称为零矩阵，m×n零 矩阵记作Omxn或O. 注意 不同阶数的零矩阵是不“相等”的， 0000 例如 0000 "≠"(000 0) 0000 0 00 0 回

（6）元素全为零的矩阵称为零矩阵， 零 矩阵记作 或 . mn Omn O 注意 " " (0 0 0 0). 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                不同阶数的零矩阵是不“相等”的. 例如

同维矩阵与矩阵相等的概念 1.两个矩阵的行数相等，列数相等时，称为同 维矩阵 12 例如 568 为同维矩阵 37 2.两个矩阵A=4,与B=b)为同维矩阵，并 且对应元素相等，即 =bg(i=1,2,,m5j=1,2,,n), 则称矩阵A与B相等，记作A=B

A与B 2..两个矩阵 为同维矩阵,并 且对应元素相等,即 ( ) ( ) ij ij A = a 与B = b a b (i 1,2, ,m; j 1,2, ,n), ij = ij =  =  则称矩阵 相等,记作 A = B. 例如                     3 9 8 4 14 3 3 7 5 6 1 2 与 为同维矩阵. 同维矩阵与矩阵相等的概念 1.两个矩阵的行数相等,列数相等时,称为同 维矩阵