
第二章复变函数 §1.复变函数的极限与连续性 设w=f(z)是确定于区城G内的单值函数,o∈G.如果对任给 的e>0,存在正数6=6(e),使得当0<|2-ol<ò时,有|f(z) A<e.我们就说当?→zo时,f(2)的极限为A记作1imf(z)=A. 特别地,如果A=f(o),我们就说函数∫()在点g处连续. 若令f(2)=(x,)+w(x,),0=xo十io,A=a十b,则从 明显不等式 0)-bSf(a)-A≤u(,)-a时+1(g0-b1 推知关系式1imf(z)=A等价于 aie,》=a,eni(,g0=b. 那么,在普通数学分析中,关于函数极限的一些初等命题对复变函 数的情形也成立、 特别地,由上述不等式知,(2)在0处连续的充要条件是,两 个二元实变数的实函数u(x,y)=Re{f()}与(x,)=Im{f(z)} 在(x0,0)处都是连续的.因而连续实函数的一些重要性质对连续 的复函数也是具有的、例如,确定在有界闭集F上的复函数f(), 它是一致连续的,它的模有界,模的上界与下界在F上可以达到, 等. 例题与习题 1.试讨论下式定义的函数的连续性: ·22·
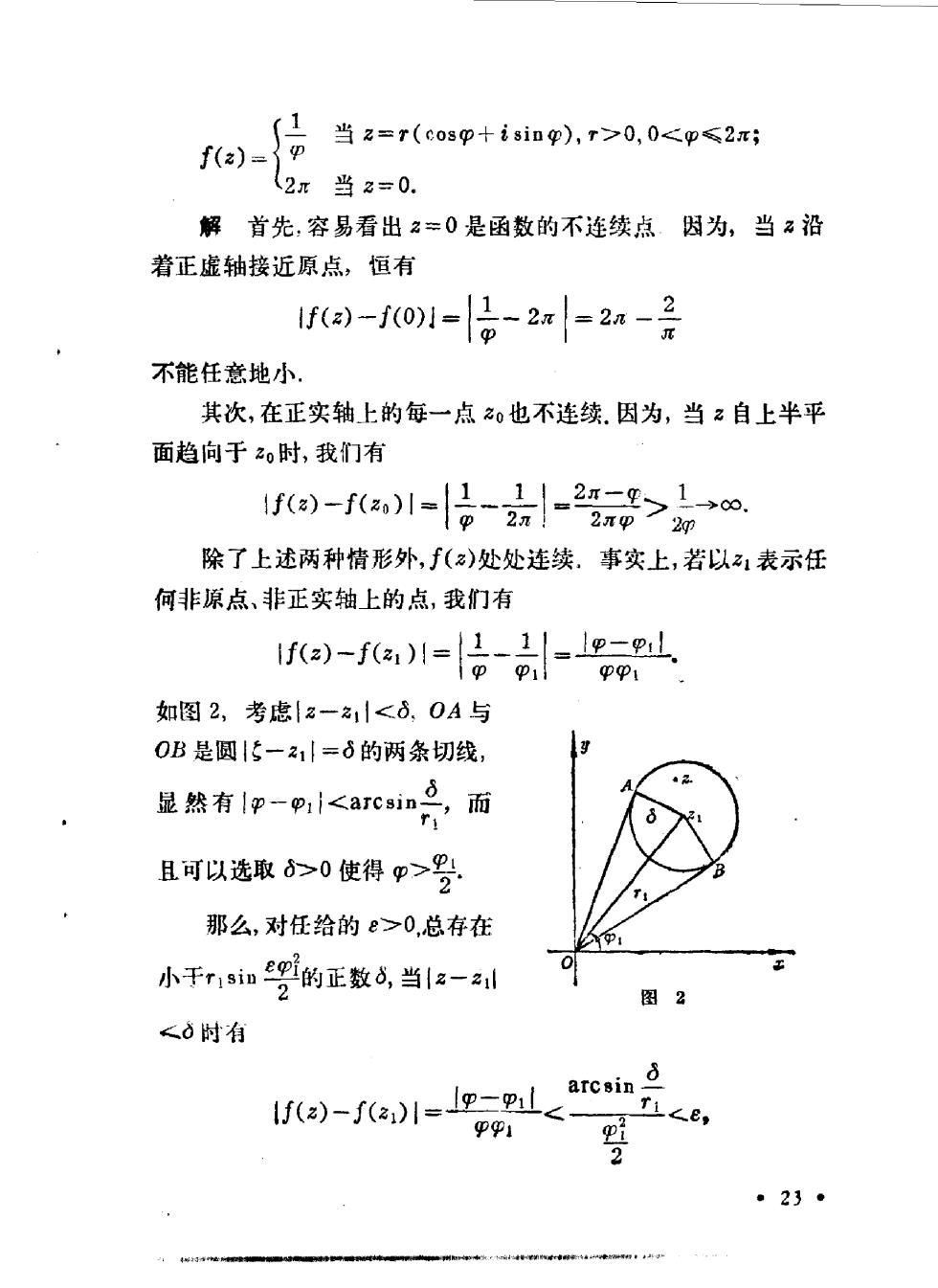
(当2=r(e0sp+ising),r>0,0<m≤2x; f()-了p 2π当2=0. 解首先,容易看出2=0是函数的不连续点。因为,当?沿 着正虚轴接近原点,恒有 )-f01-日-2x-2-景 不能任意地小。 其次,在正实轴上的每一点0也不连续.因为,当名自上半平 面趋向于0时,我们有 fe)-e1-|日2-2>女o 除了上述两种情形外,(2)处处连续,事实上,若以1表示任 何非原点、非正实轴上的点,我们有 e-,川-日-loL 如图2,考虑{2-1|<6,0A与 OB是圆|5一21|=6的两条切线, 显然有1甲-9<arc,in月面 且可以选取>0使得甲>受 那么,对任给的e>0,总存在 小千r1 sin eoi的正数d,当|z-24l 2 图2 <ò时有 a)(a)e p L人8, ·23

这就是我们所要证明的。 2.试证明连续函数f(z)的模也是连续的 证这可以从不等式 1lf()|-1f(2)1川≤1f(z)-f(2o)川 立即推得. 3.试按定义证明w=2”处处连续(%为自然数), 4.假设当名≠0时: ()(( 1()()Ro 1212 而当名=0时,上述五个函数都取零值.试问这些函数在哪些点连 续?在哪些点不连续? 5.试讨论下式定义的函数的连续性: f()=0=0时: (o =r(coso-risino),r>0,05<2z. 6.试讨论下式定义的函数的连续性: fo-npinptinr28ospca 7.若一函数加=f().当|2为无理数或零时,f(z)=0;当 1=君时(⑧,9为既约的自然数,f(e)=司试讨论它的连 续性。 8.若以1,⊙1,.,⊙m-1表示1的%个n次根,试从 2-1+2-2+.+名+1=(2-01)(2-⊙2).(2-0m-1), 所端令21,证明2-1sin名sin2.sin么1)=儿 。24·

9.试问函数: f(a)=ef.e)=1+, 在|<1内是否连续?是否一致连续? 10.若f()=e向,试问它在0<引<1内是否连续?是否 一致连续? 11.若函数∫(z)在z<1内不仅连续,而且一致连续.试证 明:当名m→o时(其中2n<1,o为边界点),极限1imf(2m)存在 而且与点列{zn}的选取无关. I2.试证明在上题条件下所确定的边界值,构成一个沿圆周 |=1的连续函数. §2.复变函数的导数 (一)若(z)是确定在域G内的单值函数,o是G内的一固 定点.如果极限 Iim a-a)=m器 ,△边 2一20 (其中△2=2一20,△0=f(0十△2)-f(2)存在时,我们就说f(2) 在点0处是可导的,该极限叫作f(2)在该点的导数,记为∫(2), 根据上述的定义与极限的性质,不难看出,在实数域中求导数 的基本运算法则,在这里也一样适用。 显然,函数∫(?)若在0处可导,一定在这点也是连续的 关于判定函数的可导性,我们有如下的重要结论. 定理:f(2)=u(x,)十i(x,)在点z存在导数的充要条件 是,u(x,)与u(x,)(作为二元实变数的实函数)在点名=(x,)可 微,而且满足下述的哥西-黎曼方程: ·25

能品器器 当定理的条件被满足时,'()可以表示成 f)-+器-产费别瑞别+盟 如果f(z)在域G内处处可导时,我们就说f()是G内的正则 函数.有时,我们也说∫()在一点?=0处是正则的,它的含意是 指在2,的某一邻域内处处可导。 ,(二)如果确定在域G内的实函数H(x,)具有直到二阶的连 续偏导数,而且满足拉普拉斯方程: △H器+-0 那么,H(,)叫做G内的调和函数.如果K(x,)也是C内的调 和函数,且与H(x,)以哥西-黎曼方程相连系着,我们就称K是H 的共轭调和函数. 如果函数∫(2)在G内正则,那么,它的实部u(,)是G内的 调和函数,虚部(x,)是u(x,)的共轭调和函数;反之,若给定一 个G内的调和函数u(,),我们可以求出无穷多个由下式定义的 共轭调和函数: -器++0 使得u(x,)+iu(x,)=f(2)在G内正则(其中20是G内任一固 定点,线积分沿G内任一连续曲线,C是任意常数). 例题与习题 1.试根据定义,讨论f()=|2的可导性。 解除2=0外,其他处处不可导.事实上,若0+0,那么 △0-f(a)-f=112-2l2=22-2n@=2+z,三-知 △名 名一20 2一20 2一20 2-20 ·26·