
第一章插值 2
2 第一章 插值
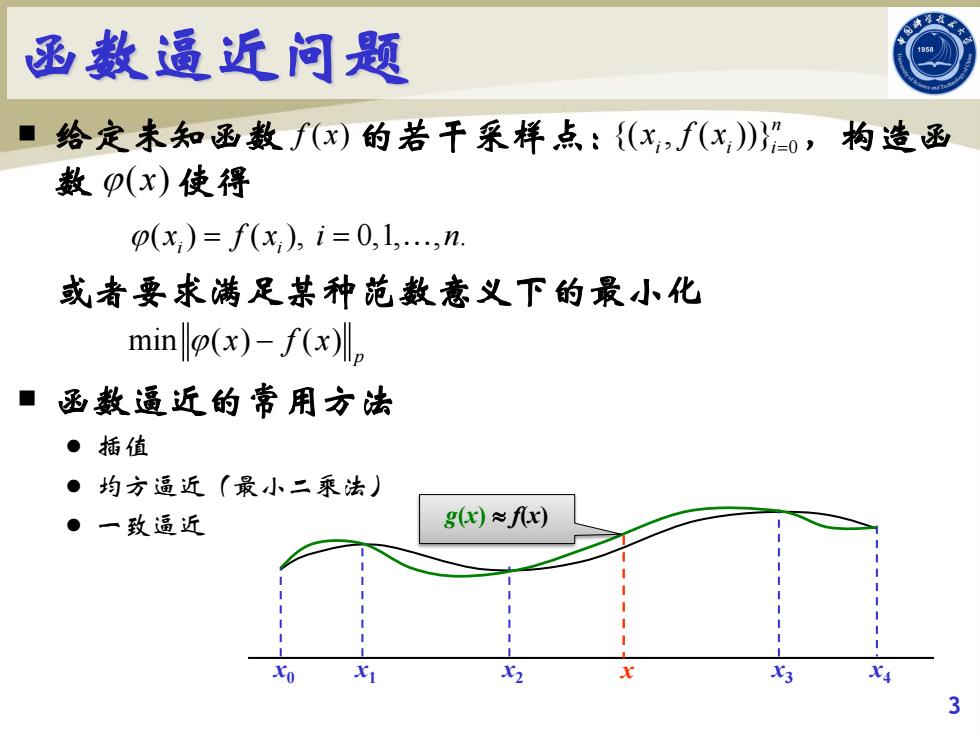
函数逼近问题 ■给定未知函数f(x)的若干采样点:{(x,f(x)}”0,构造函 数p(x)使得 p(x)=f(x),i=0,1,.,n 或者要求满足某种范数意义下的最小化 min (x)-f(x) ■函数逼近的常用方法 ●插值 ●均方逼近(最小二乘法) ●一致逼近 g(x)fx) X1 2 3
函数逼近问题 给定未知函数 的若干采样点: ,构造函 数 使得 或者要求满足某种范数意义下的最小化 函数逼近的常用方法 插值 均方逼近(最小二乘法) 一致逼近 3 f x( ) 0 {( , ( ))}n i ii x fx = ϕ( ) x ( ) ( ), 0,1, , . i i ϕ x fx i n = = min ( ) ( ) p ϕ x fx − x0 x1 x2 x x3 x4 g(x) ≈ f(x)

插值问题 1958 ■定义:f(x)为定义在区间[a,b]上的函数,xo,x1,xn为[a,b] 上+1个互不相同的点,Φ为给定的某一函数类。若Φ 上有函数p(x)满足: p(x;)=f(x),i=0,1,n 则称p(x)为f(x)关于节点o,X1,xn的插值函数 ■称X0,X,.,xn为插值节点 ■称(x,f(x)为插值型值点 ■称f(x)为被插函数
插值问题 定义: 为定义在区间 上的函数, 为 上 个互不相同的点, 为给定的某一函数类。若 上有函数 满足: 则称 为 关于节点 的插值函数 称 为插值节点 称 为插值型值点 称 为被插函数 4 f x( ) [,] a b 0 1 , , n xx x [,] a b n +1 Φ Φ ϕ( ) x ( ) ( ), 0,1, , i i ϕ x fx i n = = ϕ( ) x f x( ) 0 1 , , n xx x 0 1 , , n xx x ( , ( )) i i x fx f x( )

插值问题 ■主要问题 ●插值函数类Φ如何选取? ●插值函数p(x)是否存在? ●插值函数0(x)是否唯一? ●被插值函数f(x)与插值函数(x)之间误差如何估计? 5
插值问题 主要问题 插值函数类 如何选取? 插值函数 是否存在? 插值函数 是否唯一? 被插值函数 与插值函数 之间误差如何估计? 5 Φ ϕ( ) x ϕ( ) x f x( ) ϕ( ) x

插值问题 ■ 设p(x)=ap(x)+ap,(x)+.+a.(x),则 f(x)=(x)=aopo(x;)+ae (x)++ame (x),i=0,1.n ■ n+1个方程,m+1个未知量的线性方程组 当且仅当m=n,det(A)≠0,方程组解存在且唯一 6
插值问题 设 ,则 个方程, 个未知量的线性方程组 当且仅当 , ,方程组解存在且唯一 6 0 0 11 () () () () m m ϕϕ ϕ ϕ xa xa x a x = + ++ 0 0 11 ( ) ( ) ( ) ( ) ( ), 0,1, , i i i i mm i fx x a x a x a x i n = = + ++ = ϕϕ ϕ ϕ n +1 m +1 m n = det( ) 0 A ≠