
第二章最小二乘拟合 2
2 第二章 最小二乘拟合
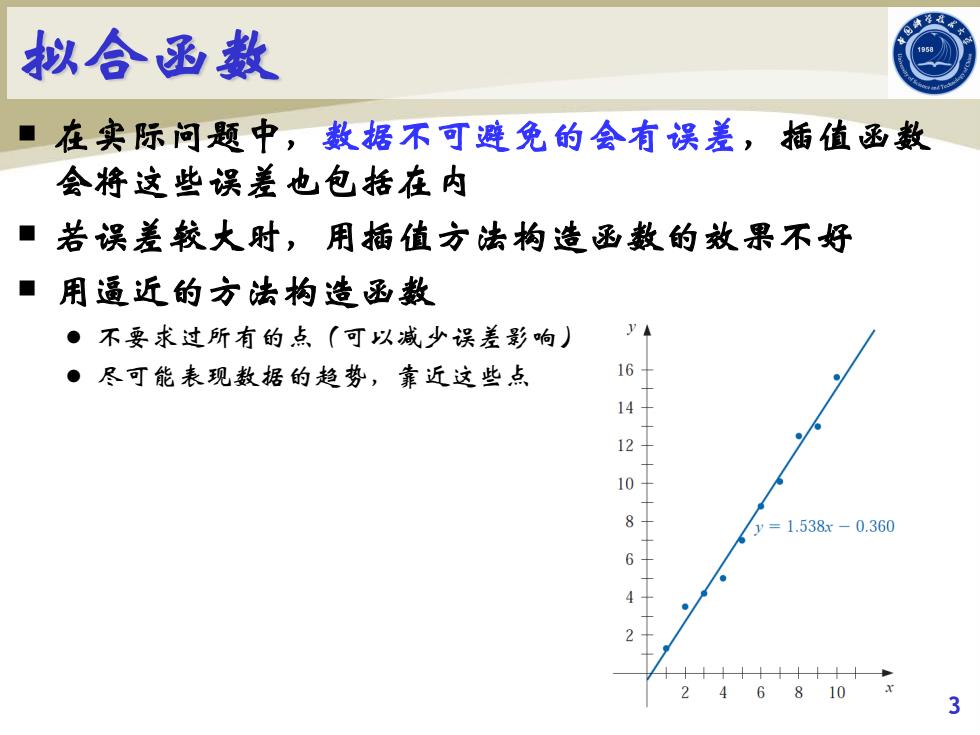
拟合函数 ■在实际问题中,数据不可避免的会有误差,插值函数 会将这些误差也包括在内 ■若误差较大时,用插值方法构造函数的效果不好 ■用通近的方法构造函数 ●不要求过所有的点(可以减少误差影响) ●尽可能表现数据的趋势,靠近这些点 16 14 12 10 8 ¥=1.538x-0.360 64 2468i0 3
拟合函数 在实际问题中,数据不可避免的会有误差,插值函数 会将这些误差也包括在内 若误差较大时,用插值方法构造函数的效果不好 用逼近的方法构造函数 不要求过所有的点(可以减少误差影响) 尽可能表现数据的趋势,靠近这些点 3

拟合函数 1958 ■如何刻画数据点和通近函数之间的靠近程度? ·给定一组观察或测量得到的一组离散数据序列{(x,y,) ,选定函数空间Φ,构造函数p(x)∈Φ,使得函数p(x)最 优的靠近高散数据序列{(x,y)%,即向量 =(p(x),p(x),p(xm)与Y=(y,2,ym)Y的误差或距离 最小 ■如何定义向量之间的距离:向量范数 R=0-Y=∑p(x)- 最小平均逼近 RQ-Y6=②x)-f 最小平方逼近 R =le-Y ll=max ((x)-y,D 最小一致逼近 1si≤m
拟合函数 如何刻画数据点和逼近函数之间的靠近程度? 给定一组观察或测量得到的一组离散数据序列 ,选定函数空间 ,构造函数 ,使得函数 最 优的靠近离散数据序列 ,即向量 与 的误差或距离 最小 如何定义向量之间的距离:向量范数 4 { } 1 (, ) m i i i x y = Φ ϕ( ) x ∈Φ ϕ( ) x { } 1 (, ) m i i i x y = ( ) 1 2 ( ), ( ), , ( ) T Q xx x = ϕϕ ϕ m 1 2 (, , , )T Y yy y = m 1 1 1 || || ( ) m i i i R QY x y ϕ = =− = − ∑ 1/2 2 2 2 1 || || ( ) m i i i R QY x y ϕ = =− = − ∑ { } 1 || || max | ( ) | i i i m R QY x y ∞ ∞ ϕ ≤ ≤ =− = − 最小平均逼近 最小平方逼近 最小一致逼近

拟合函数 Gauss:和Legendre分别发明 最小二乘法:R==o(x)- ●均方误差 ●按均方误差达到最小 ·优点:易于求解 ■最小二乘法是最基本的函数逼近方法,被广泛应用于 运筹学、统计学、通近论等各个领城 ■问题:如何选定函数空间Φ? ●专业知识或工作经验 ●观察数据 5
拟合函数 Gauss和Legendre分别发明 最小二乘法: 均方误差 按均方误差达到最小 优点:易于求解 最小二乘法是最基本的函数逼近方法,被广泛应用于 运筹学、统计学、逼近论等各个领域 问题:如何选定函数空间 ? 专业知识或工作经验 观察数据 5 2 2 2 1 ( ) m i i i RR x y ϕ = = = − ∑ Φ

线性拟合和二次拟合函数 ■最小二乘问题:给定数据序列{(x,)和函数空间 D=spani (x)(x).(x) 求函数p(x)∈Φ,使得 m∑(ox)-y)月 其中p(x)=a1p,(x)+a2p2(x)+.+anpn(x),a,∈R,i=1,2,.n ■ 若定义 0(a,4.,a,)=2(o(x)-y)'=2(a(x)+a9,(x)++a,0.(x)-y 则最小二乘问题可写成 min_Q(a1,a2,.,an) aa,.aneR 6
线性拟合和二次拟合函数 最小二乘问题:给定数据序列 和函数空间 求函数 ,使得 其中 若定义 则最小二乘问题 可写成 6 { } 1 (, ) m i i i x y = 1 2 span{ ( ), ( ), , ( )}, n Φ = ϕϕ ϕ xx x ϕ( ) x ∈Φ ( ) 2 1 min ( ) m i i i x y ϕ ϕ ∈Φ = ∑ − 11 2 2 ( ) ( ) ( ) ( ), , 1,2, nn i ϕϕ ϕ ϕ x a x a x a xa i n = + ++ ∈ = ( ) ( ) 2 2 1 2 11 2 2 1 1 (, , , ) () () () () m n n ii i i nn i i i i Qa a a x y a x a x a x y ϕ ϕϕ ϕ = = = − = + ++ − ∑ ∑ 1 2 1 2 , , min ( , , , ) n n aa a Qa a a ∈