宽带分数分频频率综合器中电荷泵和分频器电路设计 (a)本振相噪下变频影响信噪比 (b)干扰信号相噪直接影响有用信道 图2-4相位噪声的影响 那么什么是“相位噪声”?简单的说,譬如有一个周期性的正弦信号,x(⑥= Acos[wct什中n(],其中中n(①表示一个周期中变化的相位量,而我们就把这个中n() 称为“相位噪声”。相位噪声通常在频域中表征。对于一个理想的振荡器,其频 谱表现为单一频率,如图2-5()所示;而在实际的振荡器中,其频谱则表现为载 频附近的裙状,如图2-5(b)所示。 Psideband △dU Wc Wc 1Hz访 (a)理想的输出频谱 (b)实际的输出频谱 图2-5相位噪声 为了比较相位噪声的大小,需要量化相位噪声。通常,相位噪声被定义为偏 离载波附近△w处1HZ内单边带噪声功率Psideband与载波功率的Pcarier比值,用 dBc/Hz表示 C{△w}=10log Psideband(w,+△w,1Hz) (2.3) 在频率综合器的设计中,为了量化各个模块的相位噪声在整个环路中的贡 献,本论文参考了MIT的Perrot教授提出的相噪模型。其主要思路:基于整个 环路的传递函数,把各个模块的噪声贡献通过相应的传递函数在输出端求和,得 到最终输出的相位噪声[10]: PFD/CP LPF Vco Zipr(S) 9 Kvcols Divider 1/N 图2-6整数分频频率综合器的s域模型 为了方便传递函数的计算,以整数分频频率综合器为例,如图2-6所示。 8
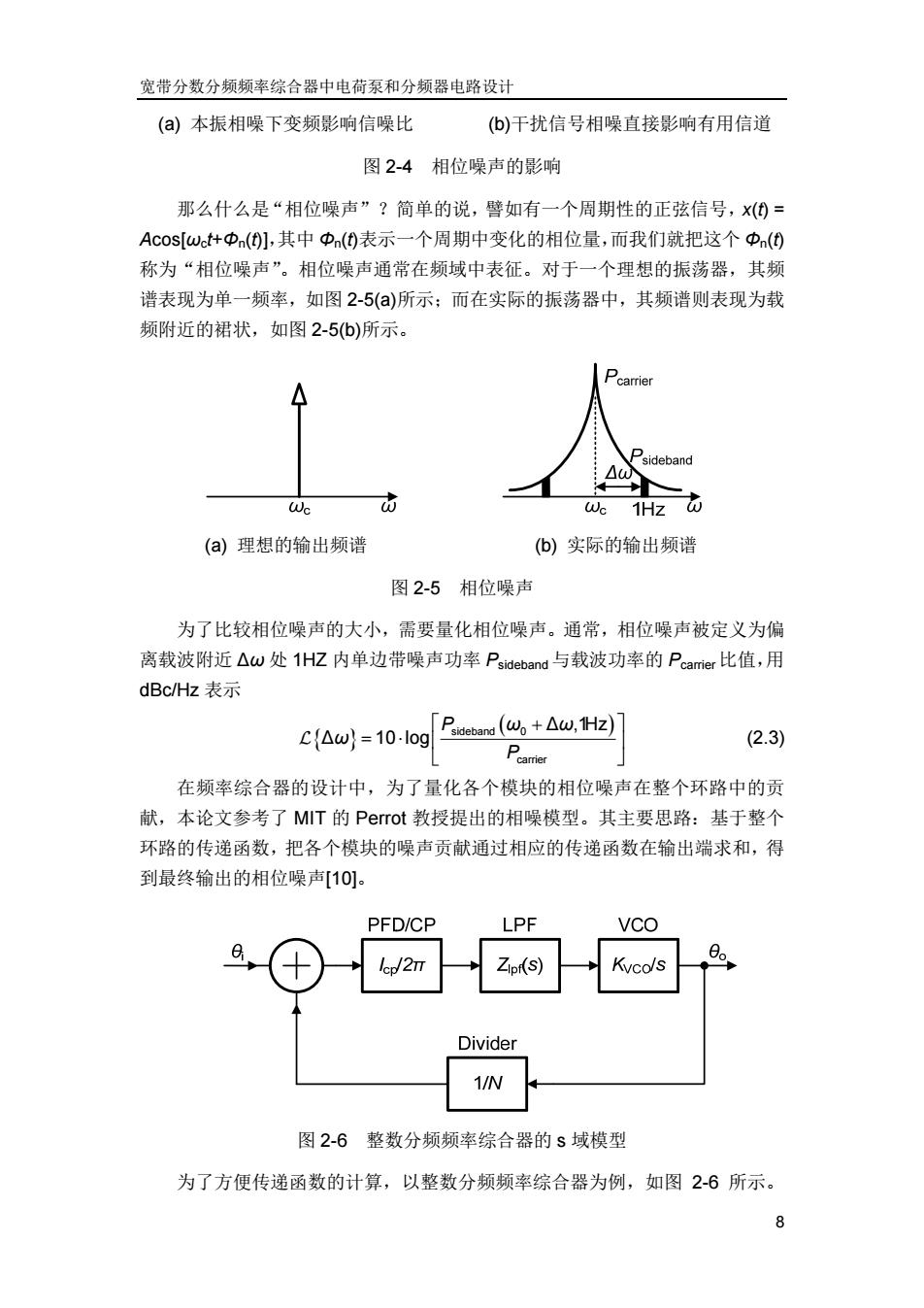
宽带分数分频频率综合器中电荷泵和分频器电路设计 8 (a) 本振相噪下变频影响信噪比 (b)干扰信号相噪直接影响有用信道 图 2-4 相位噪声的影响 那么什么是“相位噪声”?简单的说,譬如有一个周期性的正弦信号,x(t) = Acos[ωct+Φn(t)],其中 Φn(t)表示一个周期中变化的相位量,而我们就把这个 Φn(t) 称为“相位噪声”。相位噪声通常在频域中表征。对于一个理想的振荡器,其频 谱表现为单一频率,如图 2-5(a)所示;而在实际的振荡器中,其频谱则表现为载 频附近的裙状,如图 2-5(b)所示。 (a) 理想的输出频谱 (b) 实际的输出频谱 图 2-5 相位噪声 为了比较相位噪声的大小,需要量化相位噪声。通常,相位噪声被定义为偏 离载波附近 ∆ω 处 1HZ 内单边带噪声功率 Psideband 与载波功率的 Pcarrier比值,用 dBc/Hz 表示 sideband 0 carrier ∆ ,1Hz ∆ 10 log P ω ω ω P (2.3) 在频率综合器的设计中,为了量化各个模块的相位噪声在整个环路中的贡 献,本论文参考了 MIT 的 Perrot 教授提出的相噪模型。其主要思路:基于整个 环路的传递函数,把各个模块的噪声贡献通过相应的传递函数在输出端求和,得 到最终输出的相位噪声[10]。 图 2-6 整数分频频率综合器的 s 域模型 为了方便传递函数的计算,以整数分频频率综合器为例,如图 2-6 所示

第二章频率综合器 lcpJ2T表示PFD/CP的转换增益,其中lcp是电荷泵电流:Z(s)表示滤波器的输 入电流到输出电压的传递函数;KvCo/s表示压控振荡器的输入电压到输出频率 的传递函数,其中Kvco是调谐增益;1/N表示反馈回来中的传递函数,N是分 频器的分频比。 实际上,鉴于PFD/CP的开关采样特性,采用z域的离散模型才能更真实 地反映频率综合器的工作过程[11]。但是,当环路带宽小于参考频率的十分之一 时,为了方便分析,用$域模型已经可以得到很好的近以12]。 参考图2-6中整数分频频率综合器的s域模型,得到它的开环传递函数G(S) 和反馈回路的增益函数H(S) G(s)=。ZsK (2.4) 2mt.S H(s)-N (2.5) 进一步得到闭环环路的传递函数 G(s) F(s)-1+H(S)G(s) (2.6) 每个模块对整个环路的相位噪声贡献,可以通过把它的相位噪声等效到相应 模块的输入,然后经过传递函数在输出端累加得到,如图2-7模型所示。其中, 子n,是参考时钟的等效输入噪声,n.cp是鉴频鉴相器和电荷泵的等效输出噪声, npf是环路滤波器的等效输出噪声,n.vco和ndv分别是压控振荡器和分频器 的等效输出噪声。 02n.cp 02n.pf 2n.vco PFD/CP LPE VCO lep/2T Zipf(s) Kvcols θn.diw Divider 1/N 图2-7整数分频频率综合器相位噪声模型 在输出频率相对较高的频率综合器中,采用较多的是无源滤波器。为了简化 模型,我们用($)表示滤波器中电阻噪声的传递函数。类似前面的分析,我们可 以得到各个模块噪声在输出端的贡献 9
第二章 频率综合器 9 Icp/2π 表示 PFD/CP 的转换增益,其中 Icp是电荷泵电流;Zlpf(s)表示滤波器的输 入电流到输出电压的传递函数;KVCO/s 表示压控振荡器的输入电压到输出频率 的传递函数,其中 KVCO 是调谐增益;1/N 表示反馈回来中的传递函数,N 是分 频器的分频比。 实际上,鉴于 PFD/CP 的开关采样特性,采用 z 域的离散模型才能更真实 地反映频率综合器的工作过程[11]。但是,当环路带宽小于参考频率的十分之一 时,为了方便分析,用 s 域模型已经可以得到很好的近似[12]。 参考图 2-6 中整数分频频率综合器的 s 域模型,得到它的开环传递函数 G(s) 和反馈回路的增益函数 H(s) 2 cp lpf vco I Z sK G s π s (2.4) 1 H s N (2.5) 进一步得到闭环环路的传递函数 1 G s F s Hs Gs (2.6) 每个模块对整个环路的相位噪声贡献,可以通过把它的相位噪声等效到相应 模块的输入,然后经过传递函数在输出端累加得到,如图 2-7 模型所示。其中, θ2 n,i 是参考时钟的等效输入噪声,θ2 n,cp是鉴频鉴相器和电荷泵的等效输出噪声, θ2 n,lpf是环路滤波器的等效输出噪声,θ2 n,vco 和 θ2 n,div 分别是压控振荡器和分频器 的等效输出噪声。 Divider 1/N Icp/2π Zlpf(s) KVCO/s PFD/CP LPF VCO θ2 n,cp θ2 n,lpf θ2 n,vco θ2 n,div θ2 n,i θ2 n,o 图 2-7 整数分频频率综合器相位噪声模型 在输出频率相对较高的频率综合器中,采用较多的是无源滤波器。为了简化 模型,我们用 T(s)表示滤波器中电阻噪声的传递函数。类似前面的分析,我们可 以得到各个模块噪声在输出端的贡献

宽带分数分频频率综合器中电荷泵和分频器电路设计 NH(s) 2 Kuco +02 NH(s)2m +02 ni 1+H.(S) .cp 1+H.(S)1p .Ipf 1+H。(s) (2.7) 2 +2nvo +2 NH。(s) 1+H(s) .div 1+H2(s) 通过具体分析上式的传递函数,我们可以得到以下结论:参考时钟、分频器 以及鉴频鉴相器和电荷泵的噪声传递函数呈低通特性:环路滤波器的噪声传递函 数呈带通特性:而压控振荡器的传递函数本身呈高通特性。需要注意的是,压控 振荡器的噪声随着频偏的增加逐渐减小,以至于在整个传递函数中表现带通。 Phase↑ Reference Xtal Noise PFD/CP VCO/LPF Wc 图2-8频率综合器各模块的噪声分布 图28考虑了上述各个模块的噪声分布,然后在输出端得到的拟合图形。我 们可以看到在频偏较低处,主要受到参考时钟噪声的影响:在频偏更远处,主要 受到鉴频鉴相器和电荷泵的噪声的影响:在环路带宽的转折点或略高处,则主要 受到压控振荡器和环路滤波器噪声的影响。另外,如果是分数分频的频率综合器, 在带外还会有一个额外的凸起,甚至可能超过环路带宽内的噪声。 2.3.2毛刺 在理想情况下,我们需要在频率综合器的输出端得到单一频率的信号,但是 由于相位噪声和其他非理想因素的作用,实际输出的频谱如图2-9所示[13]。其 中在某些频偏上有明显的调制频率成分,称为“毛刺”。为了形象地描述这些毛 刺的影响,图右侧给出了它在时域中的抖动情况。 本小节主要介绍了△Σ分数分频频率综合器中的两个系统毛刺:分数毛刺 (Fractional Spur)和参考毛刺(Reference Spur)。 10
宽带分数分频频率综合器中电荷泵和分频器电路设计 10 2 2 2 22 2 2 ,, , , 2 2 2 2 , , 2 11 1 1 1 1 vco o o n o n i n cp n lpf o o cp o o n vco n div o o K NH s NH s π s θθ θ θ Hs Hs I Hs NH s θ θ Hs Hs (2.7) 通过具体分析上式的传递函数,我们可以得到以下结论:参考时钟、分频器 以及鉴频鉴相器和电荷泵的噪声传递函数呈低通特性;环路滤波器的噪声传递函 数呈带通特性;而压控振荡器的传递函数本身呈高通特性。需要注意的是,压控 振荡器的噪声随着频偏的增加逐渐减小,以至于在整个传递函数中表现带通。 图 2-8 频率综合器各模块的噪声分布 图 2-8 考虑了上述各个模块的噪声分布,然后在输出端得到的拟合图形。我 们可以看到在频偏较低处,主要受到参考时钟噪声的影响;在频偏更远处,主要 受到鉴频鉴相器和电荷泵的噪声的影响;在环路带宽的转折点或略高处,则主要 受到压控振荡器和环路滤波器噪声的影响。另外,如果是分数分频的频率综合器, 在带外还会有一个额外的凸起,甚至可能超过环路带宽内的噪声。 2.3.2 毛刺 在理想情况下,我们需要在频率综合器的输出端得到单一频率的信号,但是 由于相位噪声和其他非理想因素的作用,实际输出的频谱如图 2-9 所示[13]。其 中在某些频偏上有明显的调制频率成分,称为“毛刺”。为了形象地描述这些毛 刺的影响,图右侧给出了它在时域中的抖动情况。 本小节主要介绍了 ∆Σ 分数分频频率综合器中的两个系统毛刺:分数毛刺 (Fractional Spur)和参考毛刺(Reference Spur)

第二章频率综合器 Phase Random Noise Jitter Fractional Spur Reference Determined Spur Jitter △fREF fLo 图2-9输出频谱与波形的抖动 1)分数毛刺 对于一个理想的噪声整形电路,△Σ调制器的输出应该只会出现较小的毛刺。 但是当△Σ调制器的输入信号为分数时,它在数字电路中只能依靠移位来实现。 一定的截断误差削弱了输出序列的随机性。大多数△Σ分数分频频率综合器的输 出频谱中,除了有统计分布的抖动以外,还会在某些频点上出现毛刺,称为“分 数毛刺”。分数毛刺与参考时钟频率有以下关系,如公式(28)所示,其中B是△Σ 调制器中计数器的大小,M是△Σ调制器的输入,以及参考时钟频率E (2.8) 一般来说,环路带宽要远小于参考时钟频率。参考毛刺得到很大抑制,因此 分数毛刺成为主要考虑的问题。 2)参考毛刺 在分数分频频率综合器中,由于参考时钟对环路滤波器的调制,在载波频偏 ±EF及其谐波处,仍旧存在着参考毛刺。这些参考毛刺的存在,主要是由于电 荷泵的泄露电流以及上下电流的不匹配导致在鉴频鉴相器输入端存在静态的相 位差△日,并且通过压控振荡器的调制产生。参考毛刺贡献的相位噪声如公式(2.9) 所示 C(n.fReF)=20l0g I·Zpr(n·fREf)Keo (2.9) n.fRe 其中,是电荷泵的泄流电流,Z(S)是环路滤波器的传输函数,Kvo是压控振荡 器的增益,nf表示了参考频率的整数倍谐波。当环路锁定后,电荷泵的泄漏 电流可以忽略,此时电荷泵的上下电流不匹配占主导。但是,随着器件的尺寸越 来越小,在有效沟道小于100m后,泄漏电流变得越来越大,其影响就不可忽 略了。 相比较于整数分频频率综合器,分数分频频率综合器的环路是动态锁定的, 而且环路带宽相对较大,对毛刺的抑制相对较小,所以它的参考毛刺也大得多。 11
第二章 频率综合器 11 图 2-9 输出频谱与波形的抖动 1) 分数毛刺 对于一个理想的噪声整形电路,∆Σ 调制器的输出应该只会出现较小的毛刺。 但是当 ∆Σ 调制器的输入信号为分数时,它在数字电路中只能依靠移位来实现。 一定的截断误差削弱了输出序列的随机性。大多数 ∆Σ 分数分频频率综合器的输 出频谱中,除了有统计分布的抖动以外,还会在某些频点上出现毛刺,称为“分 数毛刺”。分数毛刺与参考时钟频率有以下关系,如公式(2.8)所示,其中 B 是 ∆Σ 调制器中计数器的大小,M 是 ∆Σ 调制器的输入,以及参考时钟频率 fREF 2 spur REF B M f f (2.8) 一般来说,环路带宽要远小于参考时钟频率。参考毛刺得到很大抑制,因此 分数毛刺成为主要考虑的问题。 2) 参考毛刺 在分数分频频率综合器中,由于参考时钟对环路滤波器的调制,在载波频偏 ±fREF 及其谐波处,仍旧存在着参考毛刺。这些参考毛刺的存在,主要是由于电 荷泵的泄露电流以及上下电流的不匹配导致在鉴频鉴相器输入端存在静态的相 位差 ∆θ,并且通过压控振荡器的调制产生。参考毛刺贡献的相位噪声如公式(2.9) 所示 ( ) 20log l lpf REF vco REF REF I Z nf K n f n f (2.9) 其中,Il 是电荷泵的泄流电流,Zlpf(s)是环路滤波器的传输函数,Kvco是压控振荡 器的增益,nfREF 表示了参考频率的整数倍谐波。当环路锁定后,电荷泵的泄漏 电流可以忽略,此时电荷泵的上下电流不匹配占主导。但是,随着器件的尺寸越 来越小,在有效沟道小于 100nm 后,泄漏电流变得越来越大,其影响就不可忽 略了。 相比较于整数分频频率综合器,分数分频频率综合器的环路是动态锁定的, 而且环路带宽相对较大,对毛刺的抑制相对较小,所以它的参考毛刺也大得多
宽带分数分频频率综合器中电荷泵和分频器电路设计 2.3.3锁定时间 除了相位噪声和毛刺,频率综合器的锁定时间也是一个非常关键的参数。简 单的说,锁定时间表征了一个频率综合器能够切换频率的快慢程度,一般要求在 几十毫秒到几十微秒的范围内[☑。 当频率综合器的输出频率从f变化到2时,参考时钟的频率也从fN变化 到N,近似于一个阶跃函数。通过对阶跃函数进行拉普拉斯变换并且结合闭环 传递函数(2.6),然后对其进行反傅里叶转换,得到输出频率随时间变化的函数。 为方便起见,以三阶无源滤波器为例,如图2-10(a)所示。 F(t)=5+(G-5)e5. eaoi小,5-8 (2.10) √1- 其中w和ξ分别表示系统的本振频率和瞬态响应的阻尼因子,它们的值可以分 别通过公式(2.11)和公式(2.12)得到 Wn lep·Kvco (2.11) 2m.N.(C,+C2+C3) 5-R-Cz.w (2.12) 2 最后,从公式(2.10)我们可以得到频率综合器的输出频率从变化到五所需 的锁定时间,其中△f=f-f △f V1-ξ2 -In 5-f1-2R2C25w,+R2C22ωn7 T= (2.13) ξw。 图2-10(b)形象地描述了输出频率f变化到2的瞬态过程。 Third-Order fout Transient Response of"f' Passive Filters R c,十 C (a)三阶无源滤波器 (b)频率的瞬态响应 图2-10 输出频率的瞬态响应 12
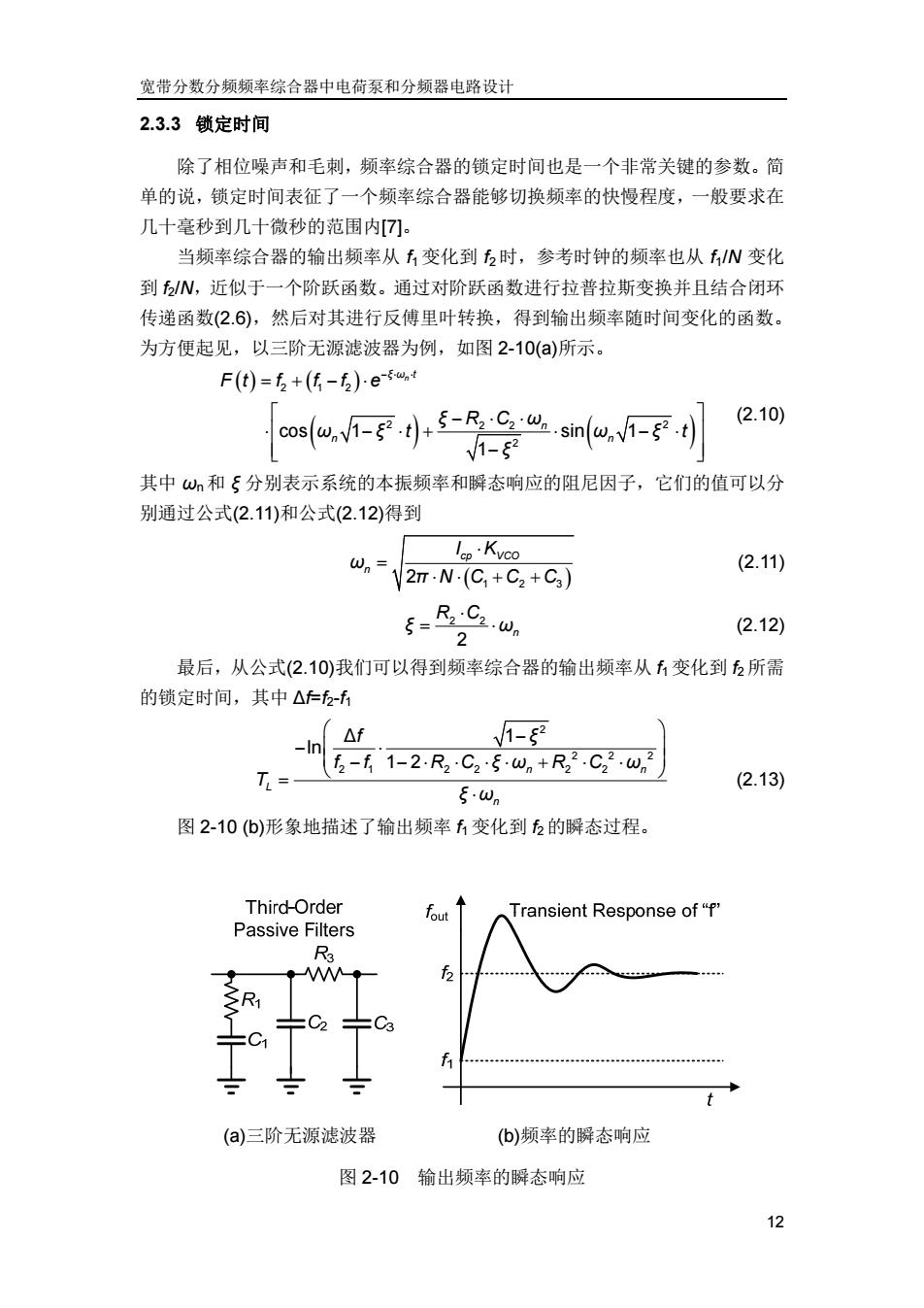
宽带分数分频频率综合器中电荷泵和分频器电路设计 12 2.3.3 锁定时间 除了相位噪声和毛刺,频率综合器的锁定时间也是一个非常关键的参数。简 单的说,锁定时间表征了一个频率综合器能够切换频率的快慢程度,一般要求在 几十毫秒到几十微秒的范围内[7]。 当频率综合器的输出频率从 f1 变化到 f2 时,参考时钟的频率也从 f1/N 变化 到 f2/N,近似于一个阶跃函数。通过对阶跃函数进行拉普拉斯变换并且结合闭环 传递函数(2.6),然后对其进行反傅里叶转换,得到输出频率随时间变化的函数。 为方便起见,以三阶无源滤波器为例,如图 2-10(a)所示。 2 12 2 2 2 2 2 cos 1 sin 1 1 n ξ ω t n n n Ft f f f e ξ R C ω ω ξ t ω ξ t ξ (2.10) 其中 ωn和 ξ 分别表示系统的本振频率和瞬态响应的阻尼因子,它们的值可以分 别通过公式(2.11)和公式(2.12)得到 2 123 cp VCO n I K ω π NC C C (2.11) 2 2 2 n R C ξ ω (2.12) 最后,从公式(2.10)我们可以得到频率综合器的输出频率从 f1变化到 f2所需 的锁定时间,其中 ∆f=f2-f1 2 22 2 21 22 2 2 ∆ 1 ln 1 2 n n L n f ξ f f RC ξ ω R C ω T ξ ω (2.13) 图 2-10 (b)形象地描述了输出频率 f1变化到 f2的瞬态过程。 (a)三阶无源滤波器 (b)频率的瞬态响应 图 2-10 输出频率的瞬态响应