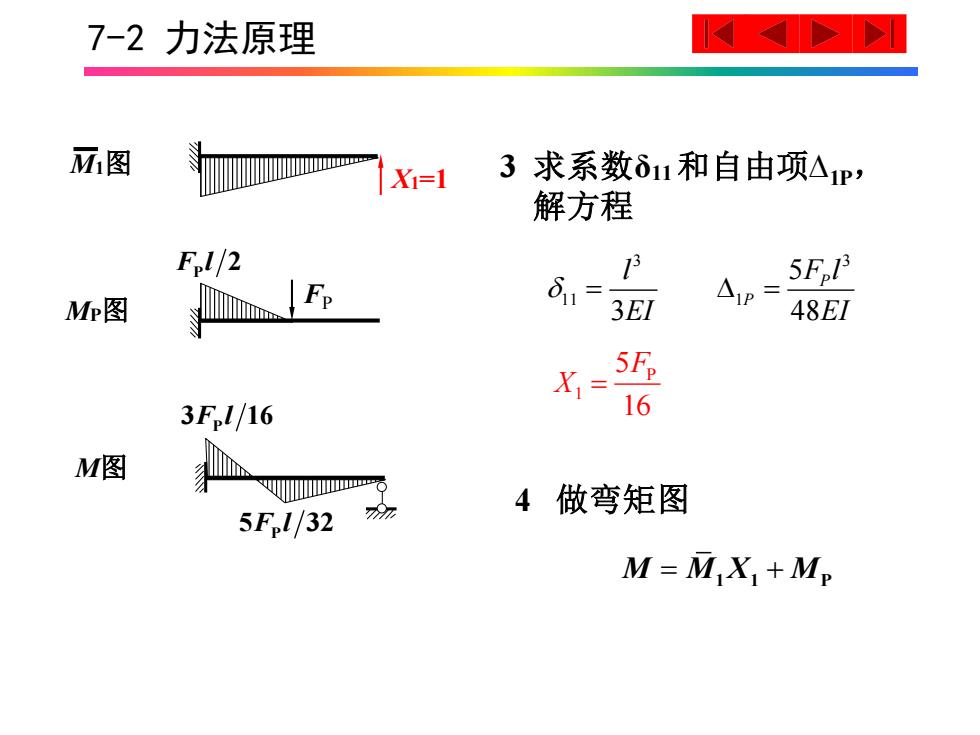
7-2力法原理 M图 Xi=1 3 求系数δ11和自由项△P, 解方程 Fl/2 5F13 Mr图 m. Fp δ=3El △1P= 48E1 5Fp 3F.l/16 X16 M图 -令 4做弯矩图 5F.l/32 M=MX +Mp
7-2 力法原理 4 做弯矩图 M M X M = + 1 1 P 3 3 11 1 5 3 48 P P l F l EI EI = = 3 求系数δ11 和自由项∆1P, 解方程 P 1 5 16 = F X M图 P 3 16 F l P 5 32 F l M1图 X1=1 MP图 FP P F l 2
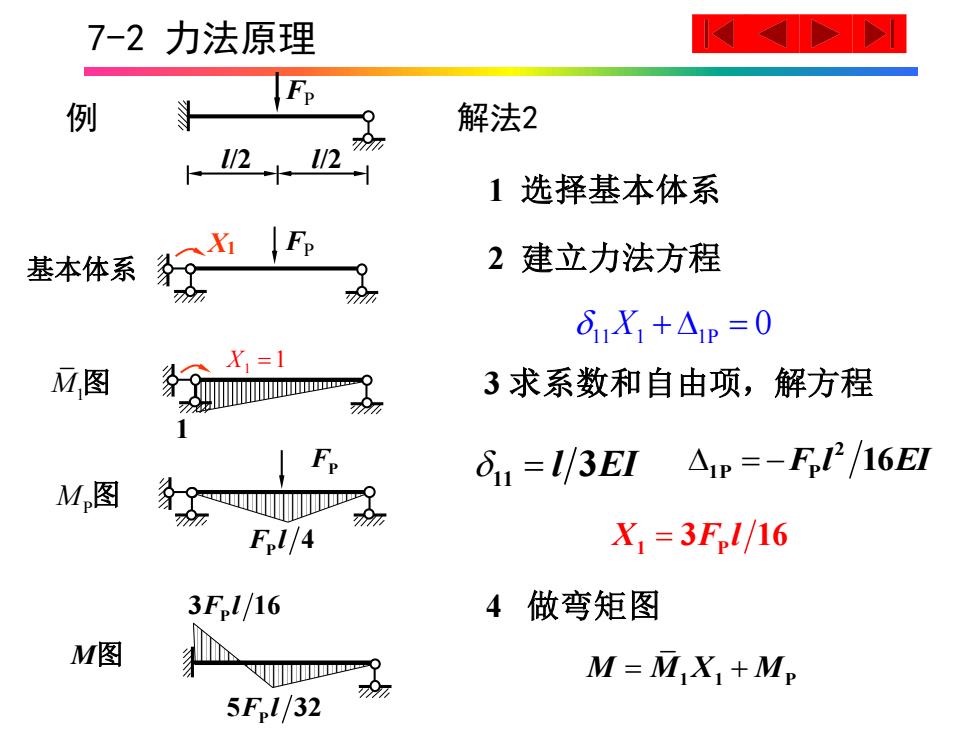
7-2力法原理 > F 例 解法2 2+2 1选择基本体系 Fp 基本体系 2建立力法方程 97 6,X+△p=0 X=1 M,图 X 3求系数和自由项,解方程 9 Fp δ1=3EIAp=-F12/16E M图 务-&严 9 F l/4 X,=3F,l/16 3F.l/16 4做弯矩图 M图 M=MX+Mp 5F.l/32
7-2 力法原理 FP 例 l/2 l/2 解法2 11 1 1P X + = 0 1 选择基本体系 2 建立力法方程 3 求系数和自由项,解方程 11 = l EI 3 = − 2 1P P F l EI 16 1 P X F l = 3 16 4 做弯矩图 M M X M = + 1 1 P M1图 1 1 X =1 X1 基本体系 FP M图 P 3 16 F l P 5 32 F l MP图 P F l 4 FP

7-2力法原理 例 解 1基本体系 M X2 2力法方程 基本体系 8uX1+62X2+△p=0 δ21X1+δ22X2+△2p=0 6 X2=1 X1=1
7-2 力法原理 X2 X1 M 基本体系 例 l l M 11 X = 1 1 21 12 22 X = 2 1 1P 2P 解 P P 11 1 12 2 1 21 1 22 2 2 0 0 X X X X + + = + + = 1 基本体系 2 力法方程
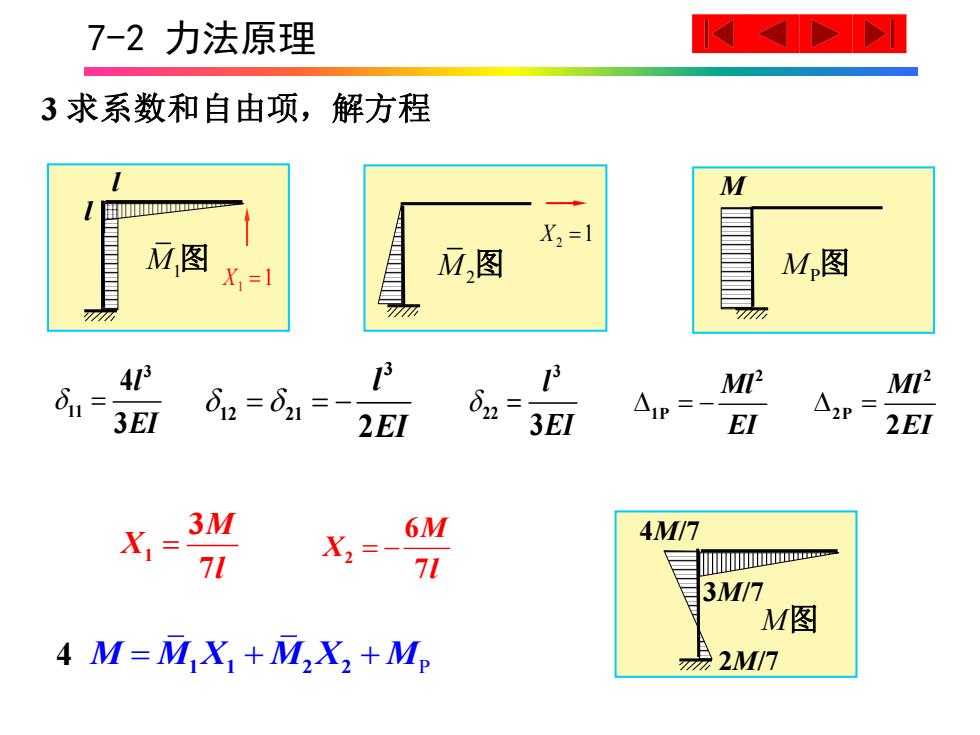
7-2力法原理 3求系数和自由项,解方程 M X2=1 M,图 X=1 M,图 M,图 43 62=d1=- 1 3 8n M MI 3EI 2EI 3EI △P= EI △2= 2EI X1= 3M 6M 11 X22- 4M/7 11 cc-一 3M/7 M图 4 M=MX +MX2+Mp 易2M/7
7-2 力法原理 M2图 2 X =1 l l 1 X =1 M1图 M MP图 4M/7 3M/7 2M/7M图 M X l 1 = 3 7 M X l 2 = − 6 7 3 求系数和自由项,解方程 l EI = 3 22 3 l EI = = − 3 12 21 2 Ml EI = 2 2 P 2 l EI = 3 11 4 3 Ml EI = − 2 1P 4 M M X M X M = + + 1 1 2 2 P

7-2力法原理 K 对于次超静定结构,力法方程为 6i1X1+612X2+.+6inXn+△1P=0 δ21X1+622X2+.+82nXn+△2p=0 6n1X1+6n2X2+.+6nnXn+△np=0 系数特点 1主系数6>0 2副系数i()可负、可正或零
7-2 力法原理 对于n次超静定结构,力法方程为 n n P n n P n n n n n n P 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 0 0 0 X X X X X X X X X + + + + = + + + + = + + + + = 1 主系数 δii>0 2 副系数 δij= δji (i≠j) 可负、可正或零 系数特点