三阶行列式的几何意义 。 它是6项的代数和,每一项都是 3个元素的乘积,其中3项为正, 另3项为负。为了便于记忆,图 3-2给出了它的计算规则。左上 到右下的三个实线箭头所经的 三个元素连乘积取正号,右上 到左下的虚线箭头所经的三个 (a13,a23,033】 元素的连乘积取负号。 三阶行列式的几何意义是以三 个三维列向量为三条边构成的 平行六面体的体积,如图3-3, (a11,021,a31) y(a12,a22,a32)
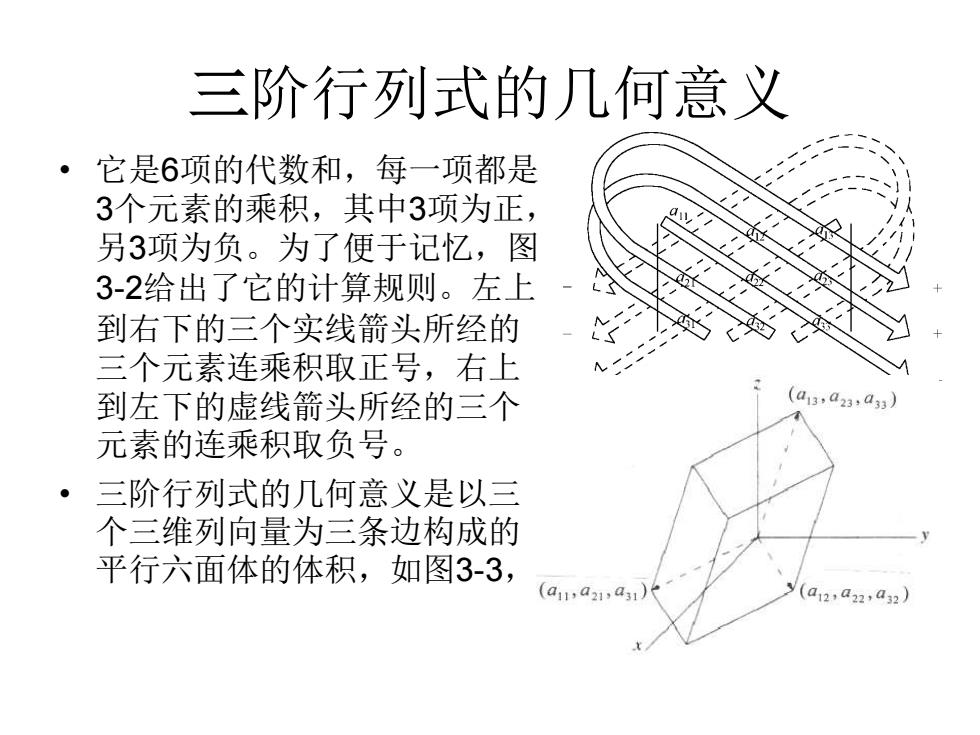
三阶行列式的几何意义 • 它是6项的代数和,每一项都是 3个元素的乘积,其中3项为正, 另3项为负。为了便于记忆,图 3-2给出了它的计算规则。左上 到右下的三个实线箭头所经的 三个元素连乘积取正号,右上 到左下的虚线箭头所经的三个 元素的连乘积取负号。 • 三阶行列式的几何意义是以三 个三维列向量为三条边构成的 平行六面体的体积,如图3-3

三阶行列式的代数特征 根据三阶行列式的定义,可以把式(3.1.5)的右端定义为D1, 再扩展到x2,X,写出 b a12413 a11 a11 az b Dx=b2 a22 a23=D,Dx3=a21b2a23=D2,Dx3=a21 a22b2=D3 b3a32 a33 a31b3433 a31 432 b3 ·当此方程组的系数行列式D0时,可以得到它的解为: X=D/D,x2=D2/D,X=D3/D。其中D1、D2、D3是用常 数项列b分别替换D中的第1、2、3列所得到的三阶行列式 如果分母上的行列式D等于零,那么解的分母就为零,其 结果是无穷大(常数0),说明其解不存在。所以,系数行 列式不等于零det(A)0也是三阶非齐次线性方程组的解存 在的必要条件
三阶行列式的代数特征 • 根据三阶行列式的定义,可以把式(3.1.5)的右端定义为D1, 再扩展到x2 ,x3,写出 • 当此方程组的系数行列式D≠0时,可以得到它的解为: x1=D1 /D,x2=D2 /D,x3=D3 /D。其中 D1 、D2 、 D3是用常 数项列b分别替换D中的第1、2、3列所得到的三阶行列式。 如果分母上的行列式D等于零,那么解的分母就为零,其 结果是无穷大(常数/0),说明其解不存在。所以,系数行 列式不等于零det(A) ≠0也是三阶非齐次线性方程组的解存 在的必要条件。 1 12 13 11 1 13 11 12 1 1 2 22 23 1 2 21 2 23 2 3 21 22 2 3 3 32 33 31 3 33 31 32 3 b a a a b a a a b Dx b a a D Dx a b a D Dx a a b D b a a a b a a a b = = = = = = ,

3.2n阶行列式定义之一:显式法 从前述的低阶行列式可以演绎出高阶行列式的定义。目前, 有三种不同的演绎方法,可形成三种定义。 (1)显式法: 根据行列式的结构直接进行演绎。二阶行列式(3.1.1)由 两项之和组成,每项为两个元素相乘;三阶行列式 (3.1.6)由六项(即3的阶乘3!)之和组成,每项为三个 元素相乘;依此类推,n阶行列式应该由n!项之和组成, 每项为个元素相乘。照此式计算时,需要做的乘法次 数为(n-1)*nl。当n=4时,3*4!=72,n=5时,4*5!=480.., 阶数略高一些,运算量更大。而演绎各项的符号规则更 加复杂,必须引入“逆序数”等概念..,很繁琐。行列 式的“可畏”,源头就在这里
3.2 n阶行列式定义之一:显式法 从前述的低阶行列式可以演绎出高阶行列式的定义。目前, 有三种不同的演绎方法,可形成三种定义。 (1)显式法: 根据行列式的结构直接进行演绎。二阶行列式(3.1.1)由 两项之和组成,每项为两个元素相乘;三阶行列式 (3.1.6)由六项(即3的阶乘3!)之和组成,每项为三个 元素相乘;依此类推,n阶行列式应该由n!项之和组成, 每项为n个元素相乘。照此式计算时,需要做的乘法次 数为(n-1)*n!。当n=4时,3*4!=72,n=5时,4*5!=480…, 阶数略高一些,运算量更大。而演绎各项的符号规则更 加复杂,必须引入“逆序数”等概念…,很繁琐。行列 式的“可畏”,源头就在这里

行列式定义之二:代数余子式法 它的思路是把显式法的表达式降阶,通过行列式按行展开的 特性,可以把n阶行列式降为n个(n-1)阶行列式。比如, 上述的三阶行列式就可以写成三个二阶行列式之和: a11 412 413 a22 a23 a, a22 D=a21 22 a2=4a2 433 +9 432 a31 a32 33 用这个方法n阶行列式的计算量为比显式法约减少n/2倍,确 定各项的正负号的规则也简化一些,但要引入更多新名 词和新概念
行列式定义之二:代数余子式法 它的思路是把显式法的表达式降阶,通过行列式按行展开的 特性,可以把n阶行列式降为n个(n-1)阶行列式。比如, 上述的三阶行列式就可以写成三个二阶行列式之和: 用这个方法n阶行列式的计算量为比显式法约减少n/2倍,确 定各项的正负号的规则也简化一些,但要引入更多新名 词和新概念。 11 12 13 22 23 23 21 21 22 21 22 23 11 12 13 32 33 33 31 31 32 31 32 33 a a a a a a a a a D a a a a a a a a a a a a a a a = = + +

行列式定义之三:对角主元连乘法 二方程组的系数矩阵,通过高斯消元法得出行阶梯形式 (3.1.1),其主对角线上两个主元的连乘积为a11a22 a12a21,正是其系数矩阵的行列式。 三阶方程组系数矩阵作高斯消元后的行阶梯形式为 au 412 a13 U=0(a142-a2a)/a1 423-413421/41 0 0 (a14203+a42,41+a134242-a1342z431-a242a3-a11a23a32)/(a1422-a242i) 其主对角线上的三个主元连乘积恰好等于其系数矩阵的三阶 行列式。由此可以推想,将n阶系数方阵用高斯消元法 变换为行阶梯形,其对角线上所有主元的连乘积就是该 方阵的行列式
行列式定义之三:对角主元连乘法 二阶方程组的系数矩阵,通过高斯消元法得出行阶梯形式 (3.1.1) ,其主对角线上两个主元的连乘积为a11a22- a12a21,正是其系数矩阵的行列式。 三阶方程组系数矩阵作高斯消元后的行阶梯形式为 其主对角线上的三个主元连乘积恰好等于其系数矩阵的三阶 行列式。由此可以推想,将n阶系数方阵用高斯消元法 变换为行阶梯形,其对角线上所有主元的连乘积就是该 方阵的行列式 ( ) ( ) 11 12 13 11 22 12 21 11 23 13 21 11 11 22 33 12 23 31 13 21 32 13 22 31 12 21 33 11 23 32 11 22 12 21 0 - / - / 0 0 ( - - - ) / - a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a a = + + U