《线性代数》课程教学资源（PPT课件，A）3-4分块矩阵

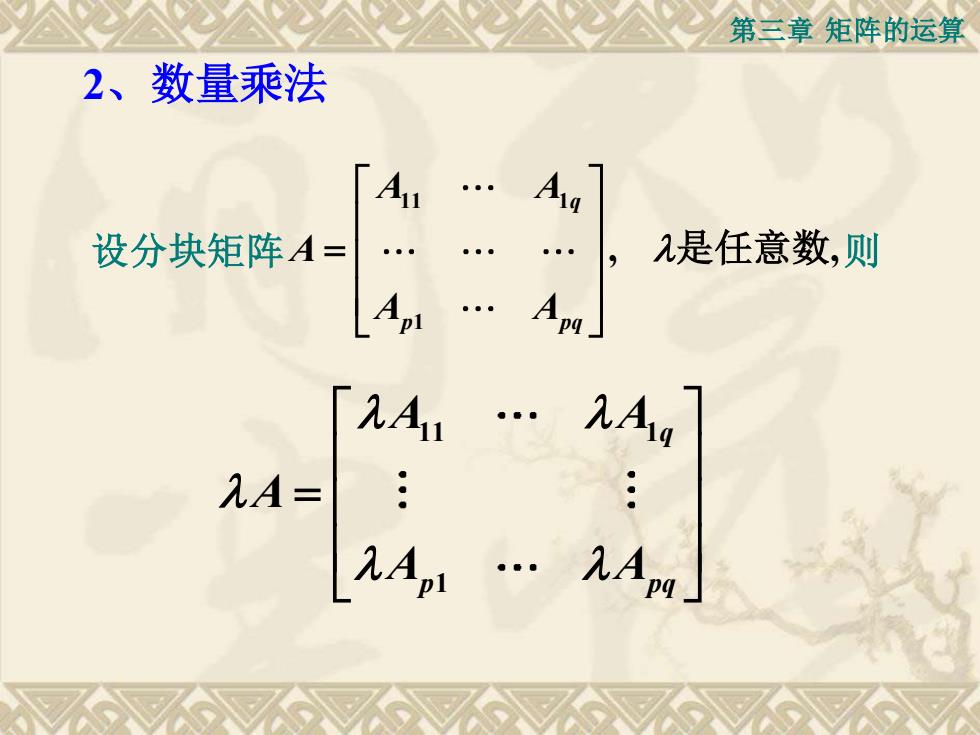
第三章矩阵的运算2、数量乘法2是任意数,则设分块矩阵A=pq2Au2AL2A=2AAq

第三章 矩阵的运算 2、数量乘法 设分块矩阵 11 1 1 , , q p pq A A A A A      =       是任意数 则 11 1 1 q p pq A A A A A          =      

第三章矩阵的运算把矩阵 A=(aik)mxs,B=(b;)xp分块成3、乘法B.1BuB=二.BBtq其中A,1,Ai2…,A,的列数分别等于Bt,B2j"B,的行数,那末AB =CCplpq其中C, -ZAiBi(i=-1,., ;j-1,.,)

第三章 矩阵的运算 11 1 11 1 1 1 1 2 1 2 , , , , , , , , , t q p pt t tq i i it j j tj A A B B A B A A B B A A A B B B         = =             其 中 的 列 数 分 别 等 于 的 行 数 那 末 ( ) 11 1 1 1 1, , ; 1, , . q p pq t ij ik kj k C C AB C C C A B i p j q =     =       其 中 = = =  3、乘法 把矩阵 ( ) , ( ) A a B b = = ik m s kj s p   分块成

第三章矩阵的运算注意：1当左边分块矩阵的列的分块方法和右边矩阵的行的分块方法一致时，分块矩阵才可以相乘2、两个分块矩阵的乘积分块矩阵的行数和列数分别等于左面分块矩阵的行数和右边分块矩阵的列数3.分块矩阵的第行第列的元素等于左边分块矩阵的第行子块与右边分块矩阵的第列子块对应相乘求和即有Ci, = A,Br, +...+ Ai,Bpjp

第三章 矩阵的运算 注意： 1、当左边分块矩阵的列的分块方法和右边矩阵 的行的分块方法一致时，分块矩阵才可以相乘. 2、两个分块矩阵的乘积分块矩阵的行数和列 数分别等于左面分块矩阵的行数和右边分块矩 阵的列数. 3.分块矩阵的第i行第j列的元素等于左边分块矩 阵的第i行子块与右边分块矩阵的第j列子块对应 相乘求和,即有 Ci j = Ai1 B1 j ++ Ai pBp j

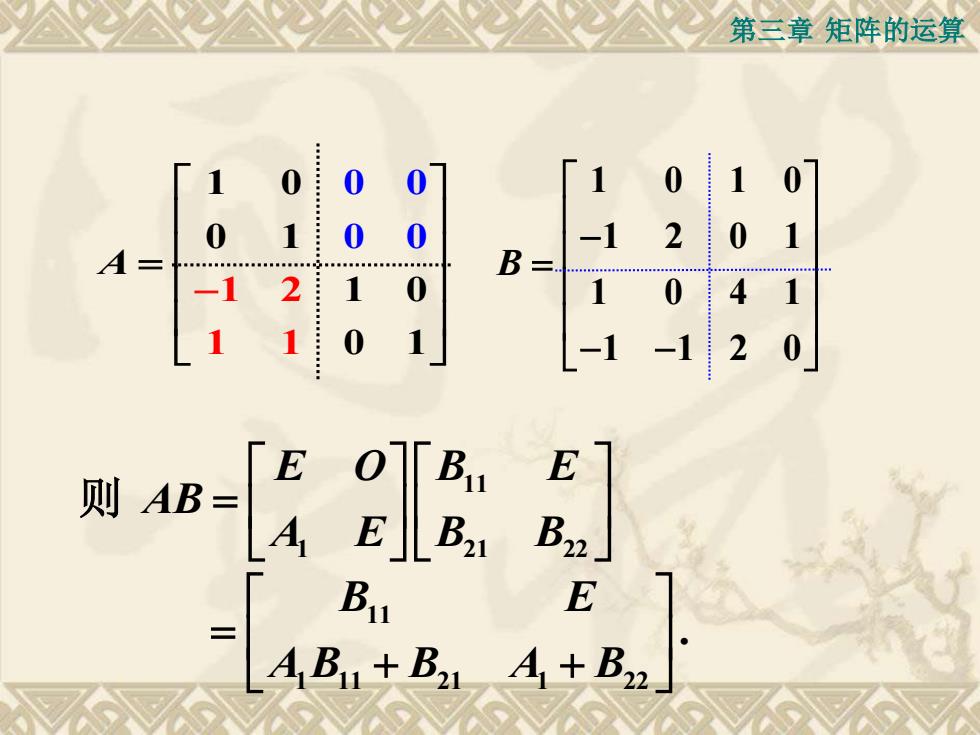
第三章矩阵的运算00007000-120B :=02110A福011E0BE11则 AB=B22B21AEB1EA +B,A,B., + B,20

第三章 矩阵的运算 1 2 1 1 0 0 1 1 0 0 0 0 1 0 0 1 A     =         − 1 0 1 0 1 2 0 1 1 0 4 1 1 1 2 0 B     − =         − − 11 1 21 22 E O B E AB A E B B     =         则 11 1 11 21 1 22 . B E A B B A B   =     + +

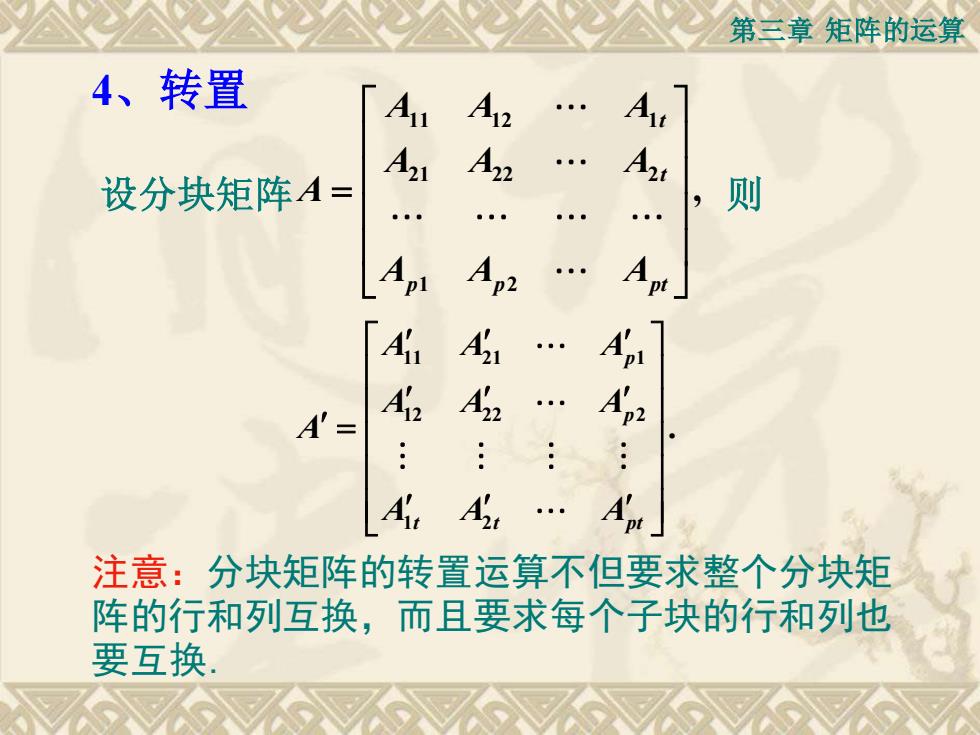
第三章矩阵的运算4、转置AnA2AA21A22A2则设分块矩阵A=AAnptA'AA'2A'DAztA'tADt注意：分块矩阵的转置运算不但要求整个分块矩阵的行和列互换，而且要求每个子块的行和列也要互换

第三章 矩阵的运算 11 21 1 12 22 2 1 2 . p p t t pt A A A A A A A A A A              =            设分块矩阵 11 12 1 21 22 2 1 2 , t t p p pt A A A A A A A A A A       =       则 4、转置 注意：分块矩阵的转置运算不但要求整个分块矩 阵的行和列互换，而且要求每个子块的行和列也 要互换