
定义2.f(x)在区间I上的原函数全体称为f(x)在I 上的不定积分,记作f(x)dx,其中 ∫一 积分号;f(x)一被积函数; (P183) x一; 积分变量;f(x)dx一被积表达式 若F'(x)=f(x),则 ∫f(x)dx=F(x)+C(C为任意常数) 例如, 「e'dx=ex+C C称为积分常数 ∫x2dx=x3+C sin xdx=-cosx+C OO▣⊙⊙8
定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. (P183) 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, = e x x d e C x + = x dx 2 x +C 3 3 1 = sin xdx − cos x +C 记作 机动 目录 上页 下页 返回 结束
不定积分的几何意义: (x)的原函数的图形称为f(x)的积分曲线 ∫f(x)dx的图形 一f(x)的所有积分曲线组成 的平行曲线族 Xo 无 Oaoo®8
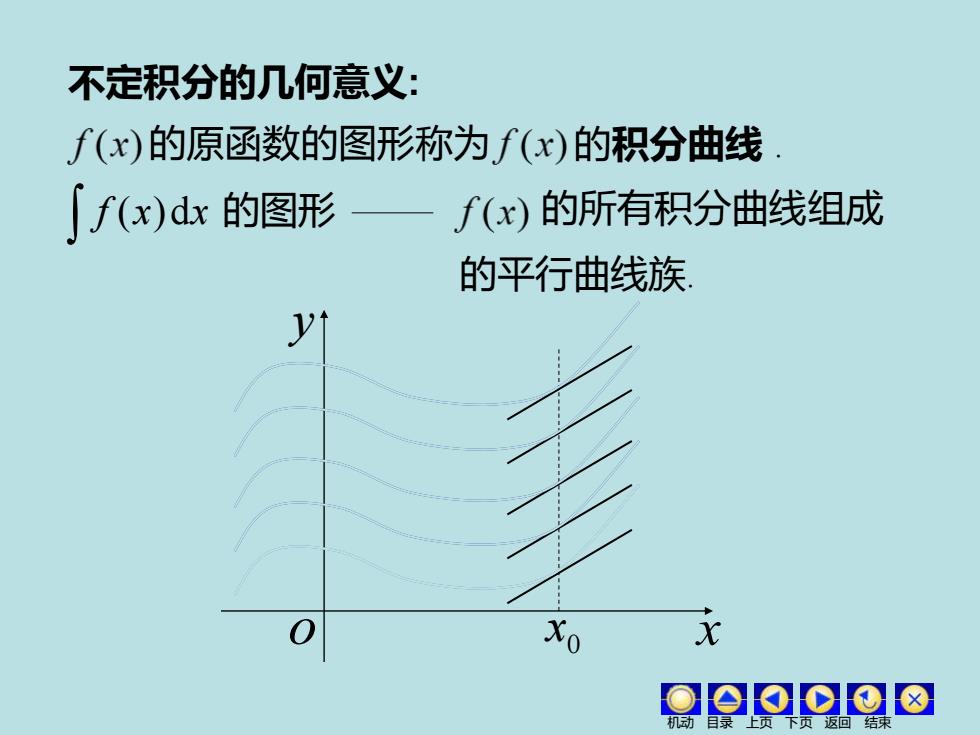
不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 机动 目录 上页 下页 返回 结束 的积分曲线

例1.设曲线通过点(1,2)且其上任一点处的切线 斜率等于该点横坐标的两倍,求此曲线的方程 解: .y=2x .y=∫2xdr=x2+C y 所求曲线过点(1,2),故有 (1,2) 2=12+C .C=1 x 因此所求曲线为y=x2+1 Ooo①C①8 机元
例1. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 1 2 y = x + 机动 目录 上页 下页 返回 结束 y o x (1, 2)

例2.质点在距地面xo处以初速vo垂直上抛,不计阻 力,求它的运动规律 解:取质点运动轨迹为坐标轴,原点在地面,指向朝上, 质点抛出时刻为t=0,此时质点位置为xo,初速为'o: 设时刻t质点所在位置为x=x(t),则 dx =v(t) (运动速度) dt x=x(t) 再由此求x(t) d2 x dv dt =-g (加速度) X0=x(0) 先由此求v(t)
o x 例2. 质点在距地面 处以初速 力, 求它的运动规律. 解: 取质点运动轨迹为坐标轴, 原点在地面, 指向朝上 , (0) 0 x = x x = x(t) 质点抛出时刻为 此时质点位置为 初速为 设时刻 t 质点所在位置为 则 ( ) d d v t t x = (运动速度) t v t x d d d d 2 2 = = −g (加速度) 机动 目录 上页 下页 返回 结束 垂直上抛 , 不计阻 先由此求 v(t) 再由此求 x(t)