
第七章 空间解析儿何与向量代数 第一部分向量代数 第二部分空间解析几何 在三维空间中: 空间形式一点,线,面 数量关系一 坐标,方程(组) 基本方法一 坐标法:向量法
数量关系 — 第七章 第一部分 向量代数 第二部分 空间解析几何 在三维空间中: 空间形式 — 点, 线, 面 基本方法 — 坐标法; 向量法 坐标, 方程(组) 空间解析几何与向量代数

第一为 第七章 向量及其钱性运算 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影 So☒
四、利用坐标作向量的线性运算 第一节 一、向量的概念 二、向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 机动 目录 上页 下页 返回 结束 向量及其线性运算 第七章

一、向量的概念 向量:既有大小,又有方向的量称为向量(又称矢量) 表示法:有向线段MM2,或a,或a. 向量的模:向量的大小,记作MM2,或a,或a: 向径(矢径):起点为原点的向量 自由向量:与起点无关的向量 M2 单位向量:模为1的向量,记作ā°或a° M 零向量:模为0的向量,记作0,或0 Oo⊙o8
表示法: 向量的模 : 向量的大小, 一、向量的概念 向量: (又称矢量). M1 M2 既有大小, 又有方向的量称为向量 向径 (矢径): 自由向量: 与起点无关的向量. 起点为原点的向量. 单位向量: 模为 1 的向量, 零向量: 模为 0 的向量, 有向线段 M1 M2 , 或 a , 机动 目录 上页 下页 返回 结束

若向量a与b大小相等,方向相同,则称a与b相等 记作a=b; 若向量a与b方向相同或相反,则称ā与b平行,记作 a川b;规定:零向量与任何向量平行; 与a的模相同,但方向相反的向量称为a的负向量, 记作-a; 因平行向量可平移到同一直线上,故两向量平行又称 两向量共线 若k(3)个向量经平移可移到同一平面上,则称此k 个向量共面
规定: 零向量与任何向量平行 ; 若向量 a 与 b大小相等, 方向相同, 则称 a 与 b 相等, 记作 a=b ; 若向量 a 与 b 方向相同或相反, 则称 a 与 b 平行, a∥b ; 与 a 的模相同, 但方向相反的向量称为 a 的负向量, 记作 因平行向量可平移到同一直线上, 故两向量平行又称 两向量共线 . 若 k (≥3)个向量经平移可移到同一平面上 , 则称此 k 个向量共面 . 记作-a ; 机动 目录 上页 下页 返回 结束
二、向量的线性运算 1.向量的加法 平行四边形法则: (a+B)+c a+b b+c a+(B+c) a d+6 三角形珍法则: a+b a a 运算规律:交换律 a+b-b+a 结合律 (a+b)+c=a+(b+)=d+b+c 三角形法则可推广到多个向量相加 Ooo⊙O8
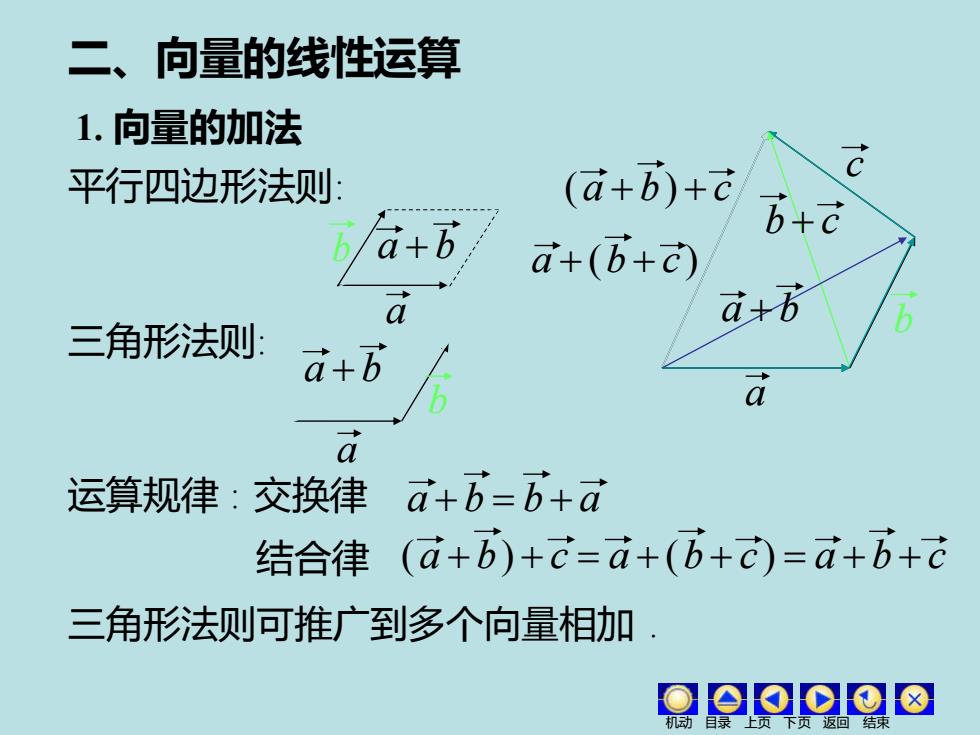
二、向量的线性运算 1. 向量的加法 三角形法则: 平行四边形法则: 运算规律 : 交换律 结合律 三角形法则可推广到多个向量相加 . 机动 目录 上页 下页 返回 结束 b b a + b = b + a (a + b) + c = a + (b + c ) = a + b + c a b c a + b b + c a + (b + c ) (a + b) + c a a a + b a + b