复变函数映射特点:把以原点为顶点的角形域映射成以原点为顶点的角形域,但张角变成为原来的n倍如果要把角形域映射成角形域,常利用幂级数元例1 映射成单位圆求把角形域0<argz<一4w<1的一个映射(w)(z)元80u
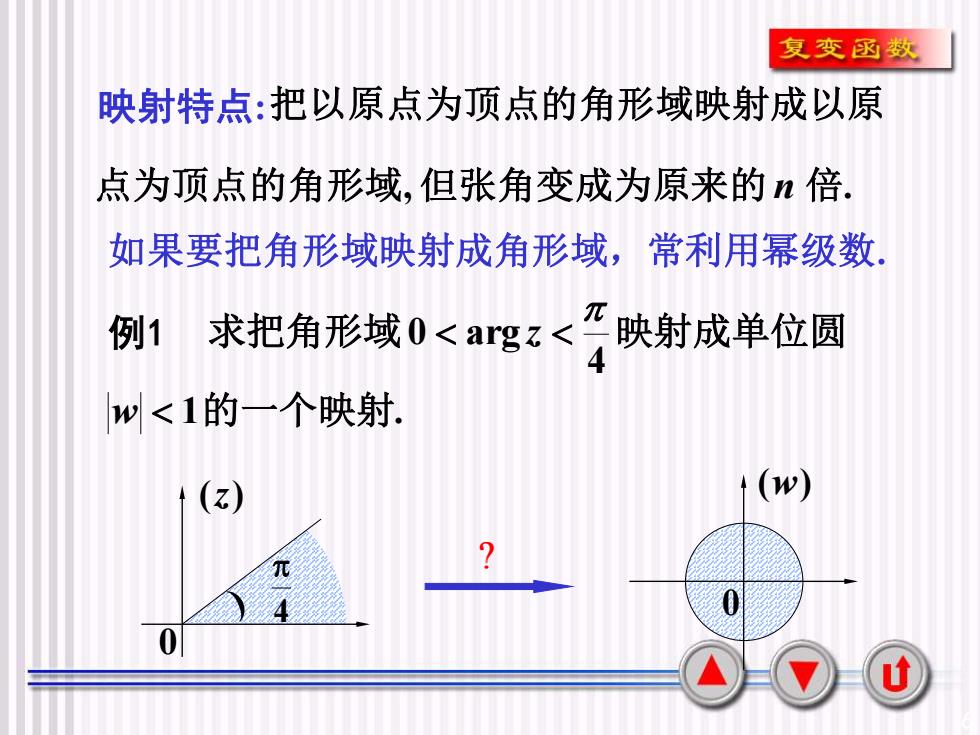
6 映射特点:把以原点为顶点的角形域映射成以原 点为顶点的角形域, 但张角变成为原来的 n 倍. 4 求把角形域0 arg 映射成单位圆 z w 1的一个映射. 0 (z) 4 ? 0 (w) 如果要把角形域映射成角形域,常利用幂级数. 例1
复变函数(5)解 (z)=Z元400S-iW=S+i因此所求映射为:(w)z4-iW=4z*+i0U
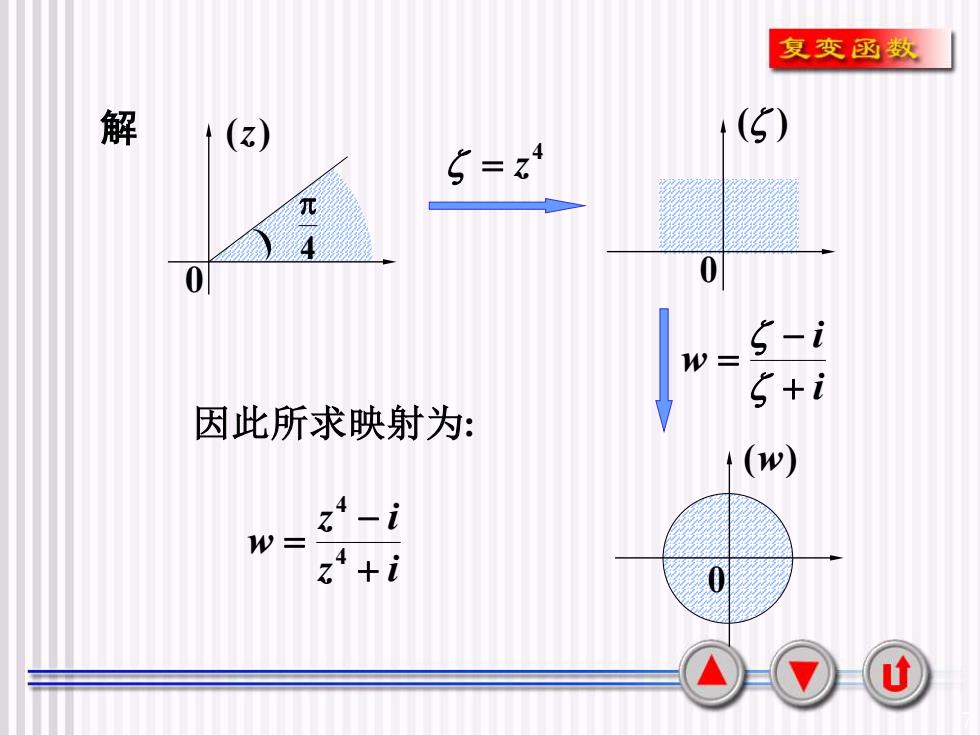
7 解 4 = z i i w + − = z i z i w + − = 4 4 0 (z) 4 0 (w) 0 ( ) 因此所求映射为:
复变函数例2 求把下图中由圆弧C,与C,所围成的交角为α的月牙域映射成角形域po<argz<P+α的一个映射.(z)(w)αSC17o0Po0u
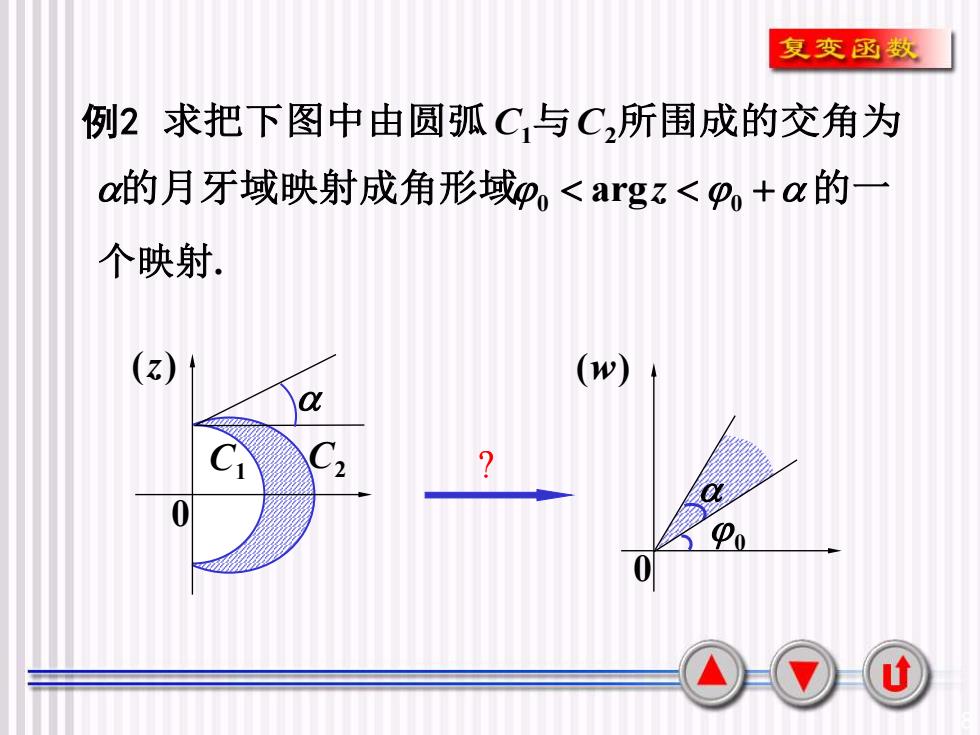
8 C 1 C2 0 ( z ) 求把下图中由圆弧C1与C2所围成的交角为 的月牙域映射成角形域0 argz 0 + 的一 个映射 . 0 ( w ) 0 ? 例 2
复变函数(z)z-i()解S= kα二z+iCC10101一C,与C,的交点为i,一 iz=i→=0, z=-i→=0,实现此步的映射是分式线性函数:z-i其中k为待定的复常数S=kz+iU
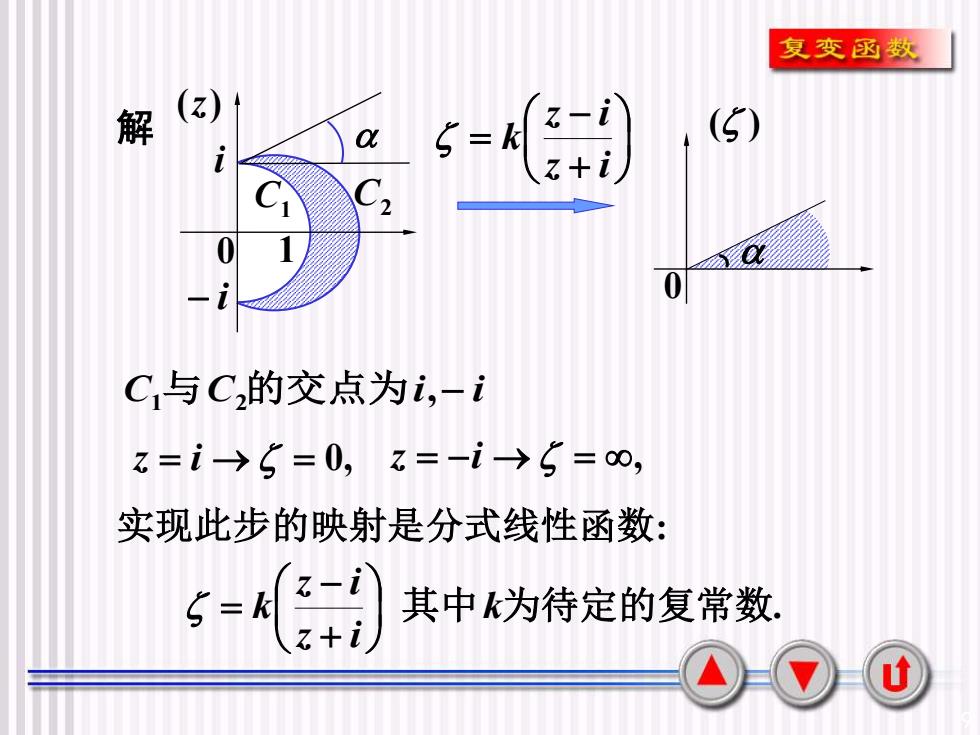
9 0 ( ) 解 − i C1 C2 0 (z) 1 , 1 2 C 与C 的交点为i − i z = i → = 0, z = −i → = , i 实现此步的映射是分式线性函数: 其中k为待定的复常数. z i z i k + − = + − = z i z i k
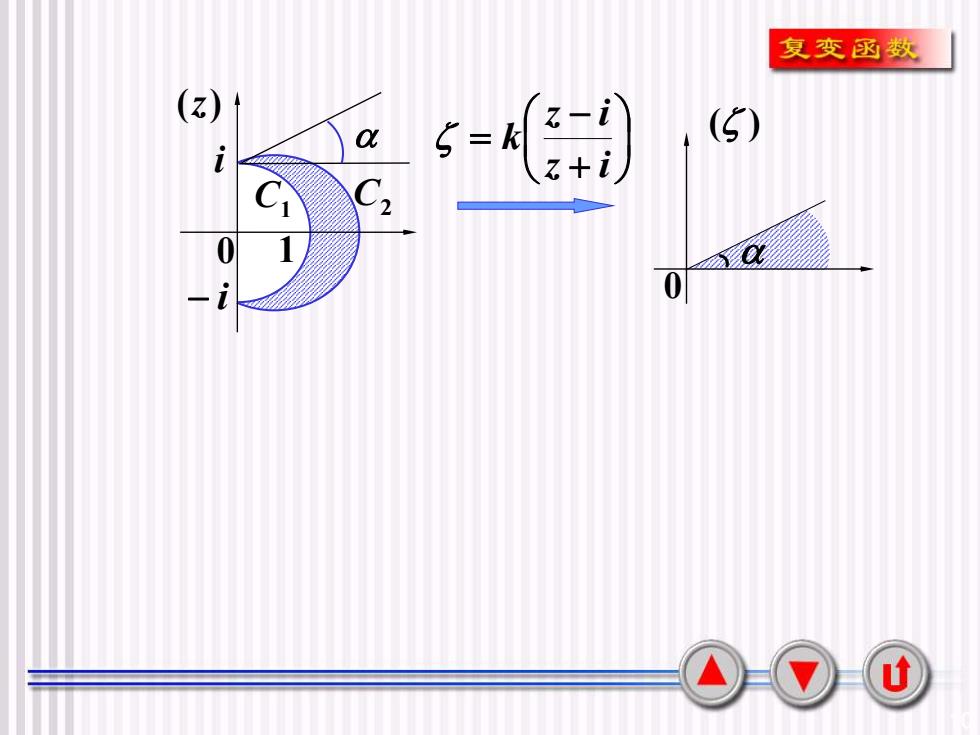
复变函数(z)z-i()=kSαz+iCC10120-U
10 0 ( ) − i C1 C2 0 ( z ) 1 i +− = z i z i k