
设f(x) eC[a,b]定理1(原函数存在定理)@(x)= (~ f(t)dt则积分上限函数是[a,b上的可导函数且对上限的导数等于被积函数在上限处的值即d(Φ(x)@(x) =f(t)dt = f(x)(a≤x≤b)dxdx从而@(x)是f(x)在[a,b]上的一个原函数x+Ar证 因为 Φ(x+x). f(t)dtT△Φ = Φ(x + 4x)-Φ(x)A
证 (x + x) = 定理1 (原函数存在定理) 设f (x)C[a,b], 则积分上限函数 且对上限的导数等于 (x)是f (x)在[a,b]上的一个原函数. 因为 是[a,b]上的可导函数, 被积函数在上限处的值.即 = = x x x d d( ( )) ( ) = x a (x) f (t)dt = f (x)(a x b) x a f (t)dt =(x + x) −(x) dx d 从而 f t t a ( )d x + x
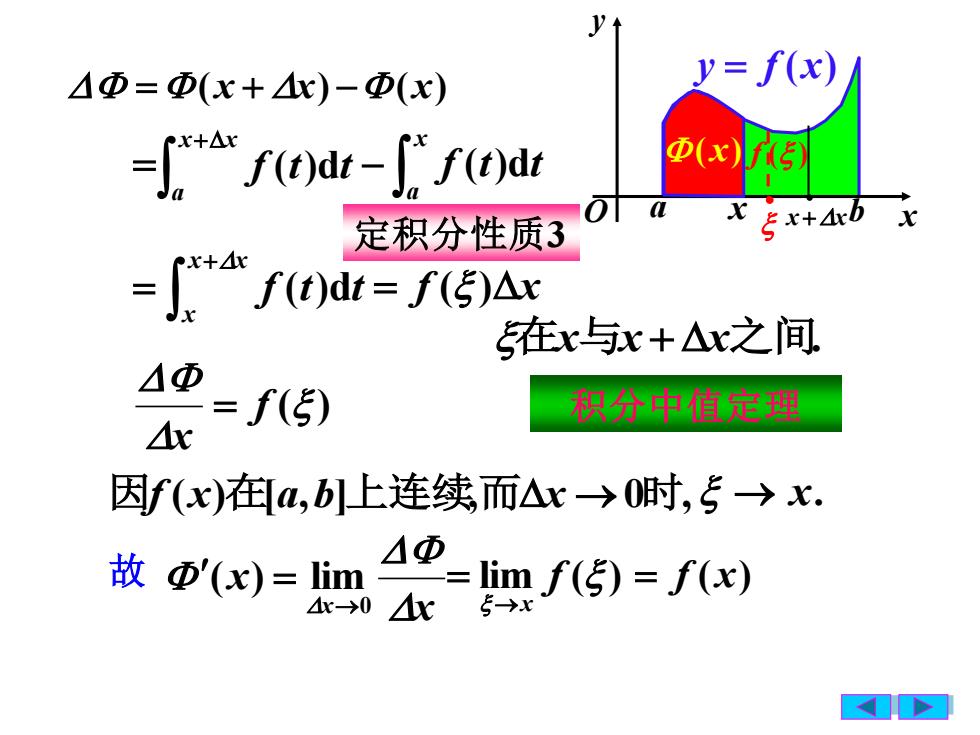
yy= f(x) △Φ = Φ(x + 4x)-Φ(x)ox+Ar)@(x)f(t)dt - (" f(t)dtfax x+4xbx三定积分性质3x+4xf(t)dt = f()Axt三在x与x+△x之间△@= f()积分中值定理4x因f(x)在[a,b]上连续而△x→0时,→x.△Φ故 @'(x)= limlim f() = f(x)Ax→4x-→>0A
=(x + x) −(x) = 在x与x + x之间. ( ) f x = 因f (x)在[a,b]上连续, x x x 0 ( ) lim → = lim ( ) f →x = = f (x) → x. 积分中值定理 = f ( )x + = x x x f t t ( )d 定积分性质3 故 而x →0时, − x a f (t)dt x+x a f (t)dt a b y = f (x) O x y x (x) f ( ) x x • + •

定理1指出:它把微分和(1)积分运算和微分运算的关系积分联结为一个有机的整体微积分,所以它是微积分学基本定理(2)连续函数f(x)一定有原函数函数Φ(x)=「 f(t)dt就是f(x)的一个原函数
定理1指出: 积分联结为一个有机的整体 (2) 连续函数 f (x) 一定有原函数, = x a (x) f (t)dt 就是f(x)的一个原函数. (1) 积分运算和微分运算的关系,它把微分和 所以它是微积分学基本定理. 函数 — 微积分

推论设f(x) EC[a,b], 函数g(x)可导,Vx E[a,b]df(t)dt = - f(x)(1)dxdrg(x)(2)f(t)dt =f[g(x)l · g'(x)dxdd[g(x) f f(t)dt)(3)g(x)f(t)dt =dxdx= g'(x). (~ f(t)dt + g(x)· f(x)drg(x)f(t)dt =dx Jh(x)dg(x)f(t)dt = f(g(x)g'(x) - f(h(x)h'(x)dxh(x)A
推论 = a x f t t x ( )d d d (1) = ( ) ( )d d d (2) g x a f t t x = x a g x f t t x ( ) ( )d d d (3) = x a g (x) f (t)dt g(x) − f ( x) f[g(x)] g(x) = ( ) ( ) ( )d d d g x h x f t t x x a f (t)dt dx d + g(x) f (x) 设f (x)C[a,b], 函数g(x)可导,x[a,b]. d d d ( ) ( ) ( ) ( ( )) ( ) ( ( )) ( ) g x h x f t t f g x g x f h x h x x = −

tdt,求f'(x).例 设f(x)=J+t+1x解 f'(x)=x2+x+11例 设f(x)=dt,求f'(x).sinx1+11uu=sinxsinxdt解 f(x)=dt21+1duddtdudx1-cosxcosx1+sin’x1+u
例 d , ( ). 1 ( ) 0 2 t f x t tt f x x + + = 设 求 解 f (x) = 例 d , ( ). 1 1 ( ) 2 sin 2 t f x t f x x + = 设 求 解 u = sin x f ( x ) = f ( x ) = + − u t t 2 2 d 1 1 t t x d 1 sin 1 2 2 + − xudd xx2 1 sin cos +− x = u cos 1 1 2 + = − + − u t u t 2 2 d 1 1 dd 1 2 x + x + x