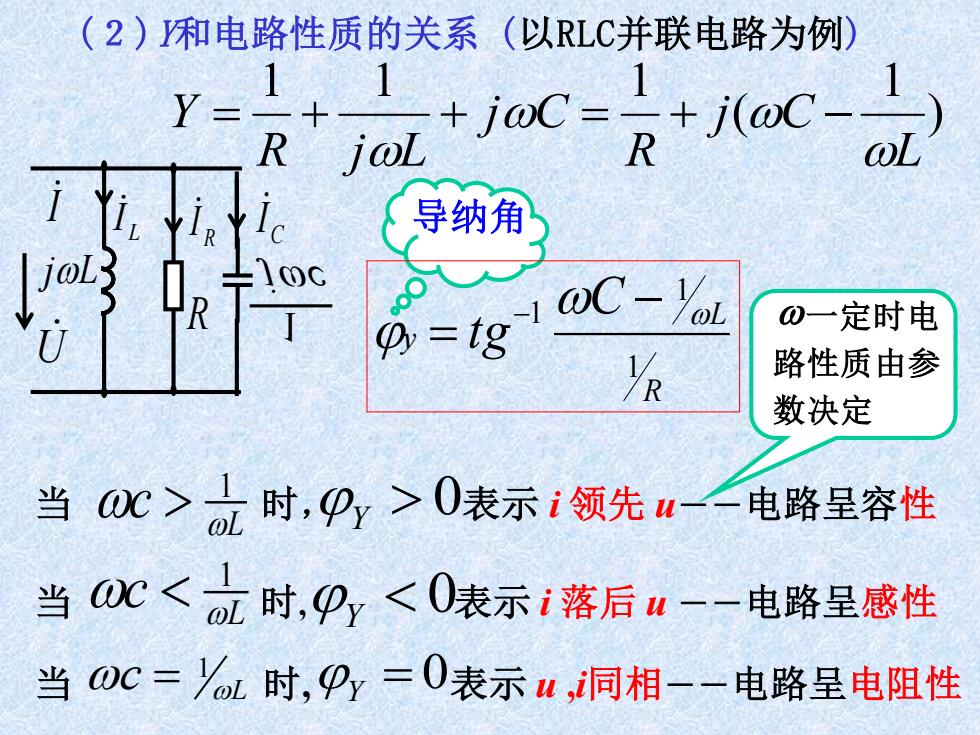
(2)和电路性质的关系(以RLC并联电路为例) Y= 1+1 R joL 导纳角 o R oy=tg aC-Yol. 0一定时电 路性质由参 数决定 当0C>L时,P,>0表示i领先u-电路呈容性 当0C<时,9,<0表示i落后w-电路呈感性 当0c=%L时,Py=0表示u,同相-一电路呈电阻性
(2)Y和电路性质的关系 (以RLC并联电路为例) ) 1 ( 1 1 1 L j C R j C R j L Y = + + = + − 一定时电 路性质由参 数决定 I 导纳角 L I R I C I jL jc 1 R R L y C tg 1 1 1 − = − 当 c L 时, 表示 i 领先 u--电路呈容性 1 Y 0 c L 当 = 1 时, Y = 0表示 u ,i同相--电路呈电阻性 L c 1 当 时, Y 0 表示 i 落后 u --电路呈感性 U
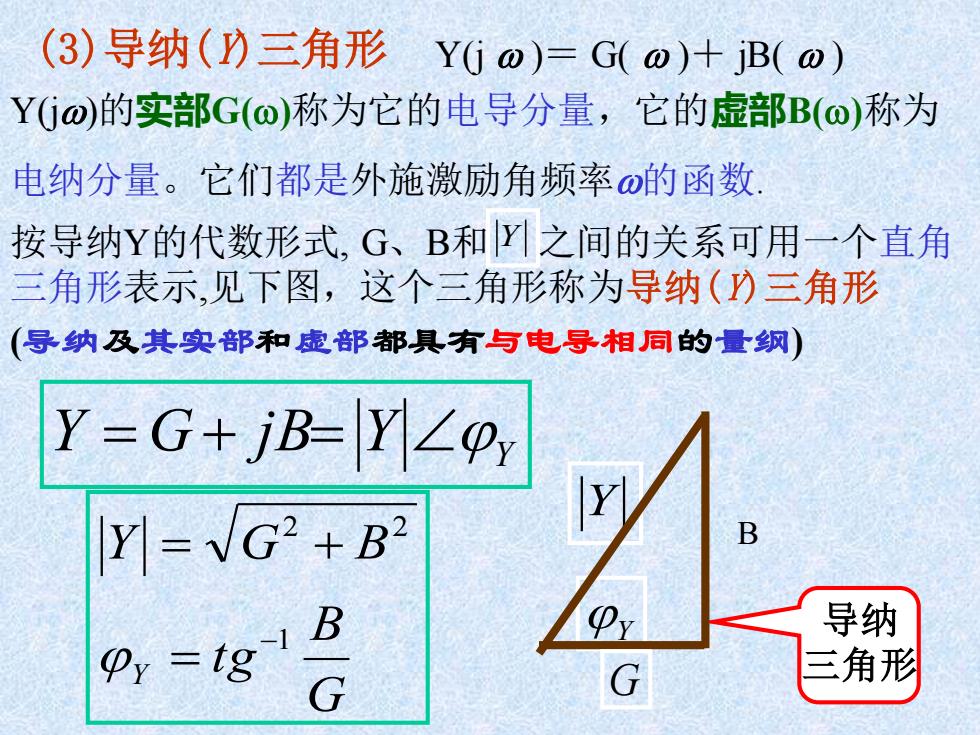
(3)导纳()三角形YGo)=G(o)+B(o) YGo)的实部G(o)称为它的电导分量,它的虚部B(o)称为 电纳分量。它们都是外施激励角频率的函数 按导纳Y的代数形式,G、B和Y之间的关系可用一个直角 三角形表示,见下图,这个三角形称为导纳()三角形 (导纳及其实部和虚部都具有与电导相同的量纲) Y=G+jB-=Y∠p Y=VG2+B2 B m (5 导纳 Py =tg 三角形
(3)导纳(Y)三角形 导纳 三角形 G B tg Y G B Y 1 2 2 − = = + Y Y Y = G + jB= Y(j )= G( )+ jB( ) Y Y G B Y(j)的实部G()称为它的电导分量,它的虚部B()称为 电纳分量。它们都是外施激励角频率的函数. 按导纳Y的代数形式, G、B和 Y 之间的关系可用一个直角 三角形表示,见下图,这个三角形称为导纳(Y)三角形 (导纳及其实部和虚部都具有与电导相同的量纲)

§9-21 阻抗(导纳)的串联和并联 阻扰的串联 z动l0 等效 z0lo: 101-4+2 0=0+0,=i(Z+Z2)=iz Z=Z+Z2=(R+X)+(R2+jX2) =∑Rx+j∑Xx X取正,X取负 4-2 20 i+Z
一 . 阻抗的串联 §9-2 阻抗(导纳)的串联和并联 Z I U U U U I Z Z IZ = 1 + 2 = ( 1 + 2 ) = = + = + = + + + K X K R j Z Z Z (R jX ) (R jX ) 1 2 1 1 2 2 XL取正,XC取负 等效 Z1 Z2 U I U1 U 2 U Z Z Z U 1 2 2 2 + = 1 2 Z = Z + Z

二 阻抗的并联 1i2 等效 z0z0→ 2言 11,1 即Z=Z∥Z2= Z,22 Z +Z
Z1 Z2 I 2 I U 1 I ( ) 1 2 1 2 1 2 1 1 Z Z U Z U Z U I = I + I = + = + Z I U 二. 阻抗的并联 1 2 1 1 1 Z Z Z = + 1 2 1 2 1 2 // Z Z Z Z Z Z Z + 即 = = 等效 Y1 Y2
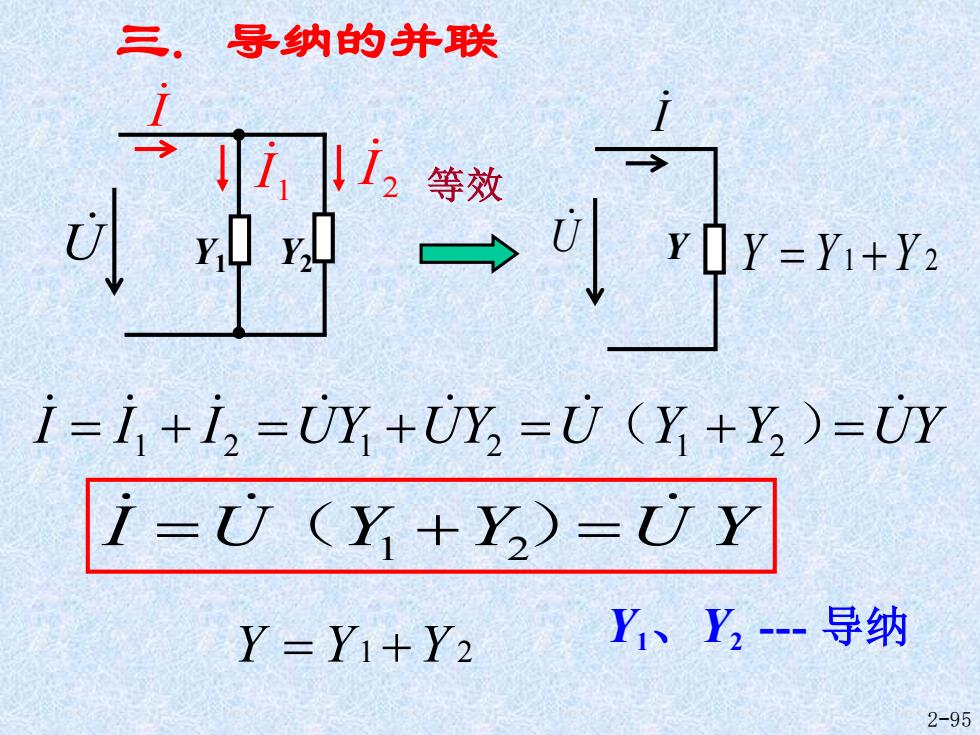
三,导纳的并联 ii2等效 中4一→0y=y+ i=i+i,=UY+UY,=U(Y+Y)=UY i=U(Y+Y)=UY Y=Y1+Y2 Y、Y2-导纳 2-95
Y1 Y2 I 2 I U 1 I I = I 1 + I 2 =U Y1 +U Y2 =U (Y1 +Y2 )=U Y Y I U 三. 导纳的并联 Y = Y1+Y 2 等效 2-95 Y = Y1+Y 2 Y1、Y2 - 导纳 I =U (Y1 +Y2 )=U Y